Self-supervised subaction Parsing Network for Semi-supervised Action Quality
论文题目:Self-supervised subaction Parsing Network for Semi-supervised Action Quality
作者:Kumie Gedamu, Yanli Ji*, Yang Yang, Jie Shao, Heng Tao Shen
单位:中山大学
期刊名称:IEEE Transactions on Image Processing
中科院分区:1区
笔记
文章文风很好,写作方法可以学习,但是很多内容介绍不仔细,K-mean算法也有用。
论文阅读
介绍
介绍完全监督AQA任务的局限性,手工标注成本很好,作者使用师生网络获取一致性的语义表示。
减少背景的依赖,
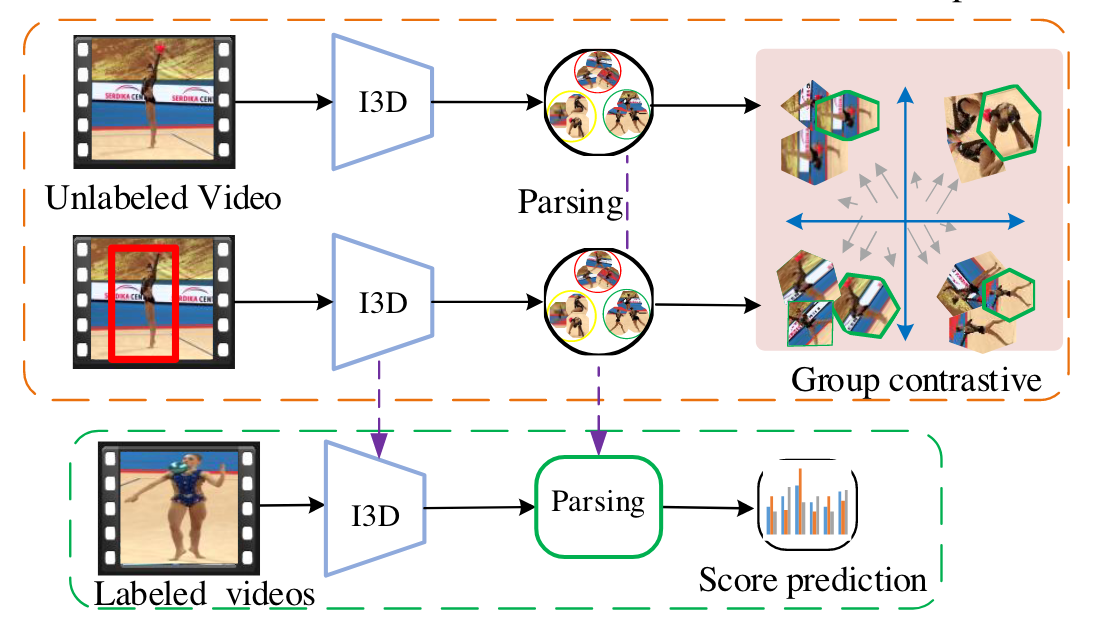
相关工作
提出的方法
整体结构:
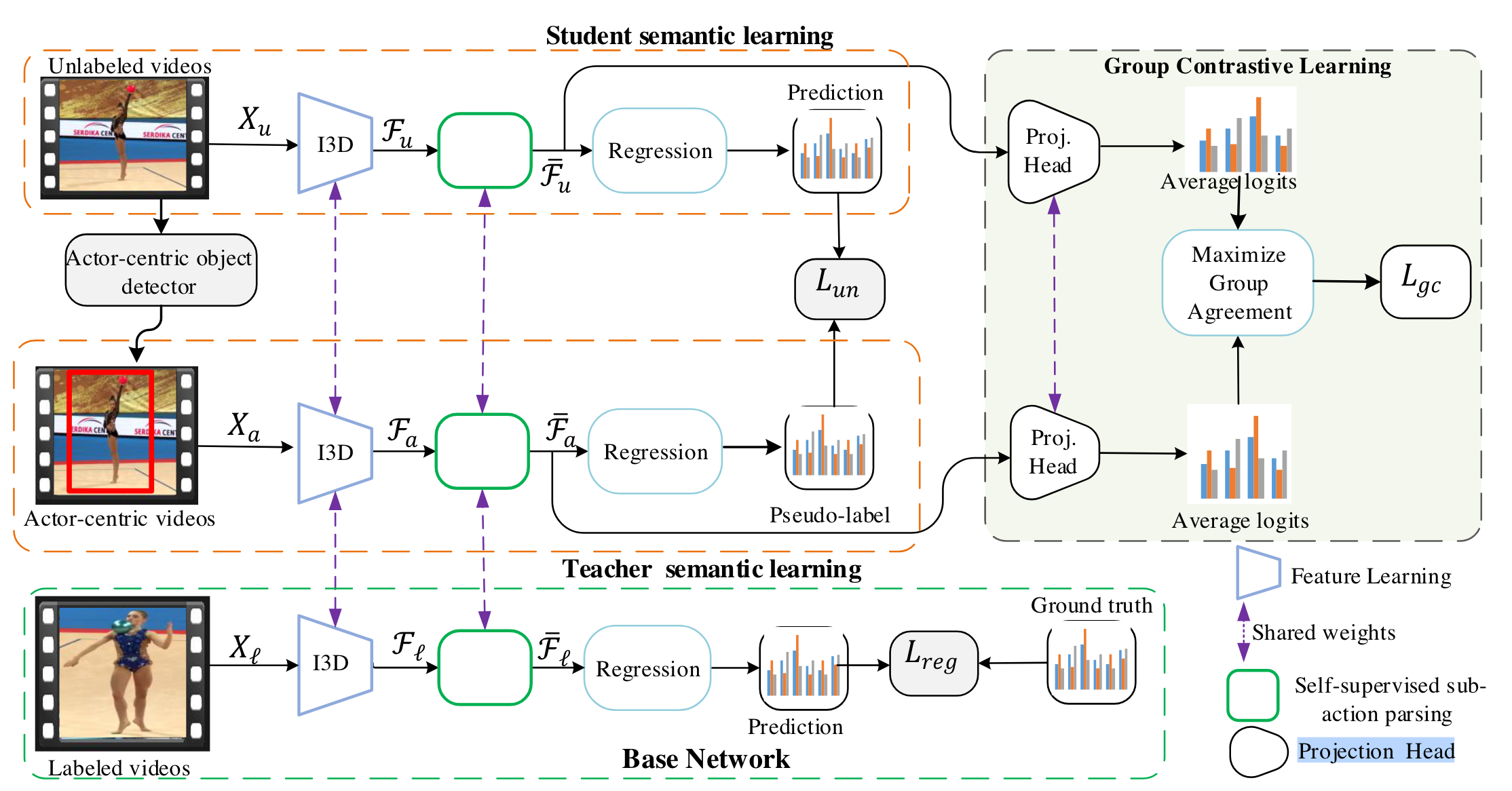
A.初步定义
标注数据集:
$X_\ell=\{x_i^\ell,y_i\}_{i=1}^{\mathbb{N}_\ell},x_i^\ell\in\mathbb{R}^{T\times H\times W\times C}$
$y_i$:标签的语义分数
未标注数据集:
$X_{u} = \{x_{i}^{u}\}_{i=1}^{\mathbb{N}_{u}}, x_{i}^{u} \in \mathbb{R}^{T\times H\times W\times C}$
$\mathbb{N}_u\gg{\mathbb{N}_\ell}$
教师模型生成预测区域,提取出特征:
$X_{a}=\{x_{i}^{a}\}_{i=1}^{\mathbb{N}_{u}}$
I3D作为骨干网络:共享参数$\theta$
$\mathcal{F}_u=E_\theta(X_u),\quad\mathcal{F}_a=E_\theta(X_a),\quad\mathcal{F}_\ell=E_\theta(X_\ell)$
B. 半监督AQA的师生网络
上两分支是学生网络,下面是教师网络。
teacher:先生成预测区域regions。
student:生成pseudo label,pseudo — prediction, 伪标签与预测的差异最小化。
回归损失:
$
\begin{aligned}
L_{un}=-\frac{1}{\mathbb{N}_{u}}\sum_{i=1}^{\mathbb{N}_{u}}||R_{\vartheta}\left(\bar{\mathcal{F}}_{u}\right)-(1\max\left(R_{\vartheta}\left(\bar{\mathcal{F}}_{a}\right)\right)\geq\tau)||^{2}
\end{aligned}$
$\max\left(R_{\vartheta}\left(\bar{\mathcal{F}}_{a}\right)\right)$ :先求回归结果的最大值,超过阀值为1,否则为0
L2 范数的平方(欧几里得距离的平方)
目的是:类似一致性规则化,让学生的预测接近伪标签。
C. 自监督子动作解析
目标是识别子动作的独特模式及其时间依赖性,并学习动作的时空结构以实现更好的表示。
假设有$K$个子动作,作者希望识别视频的所有帧到每个子动作集。
模块由两部分组成:
一:Pseudo-label generation
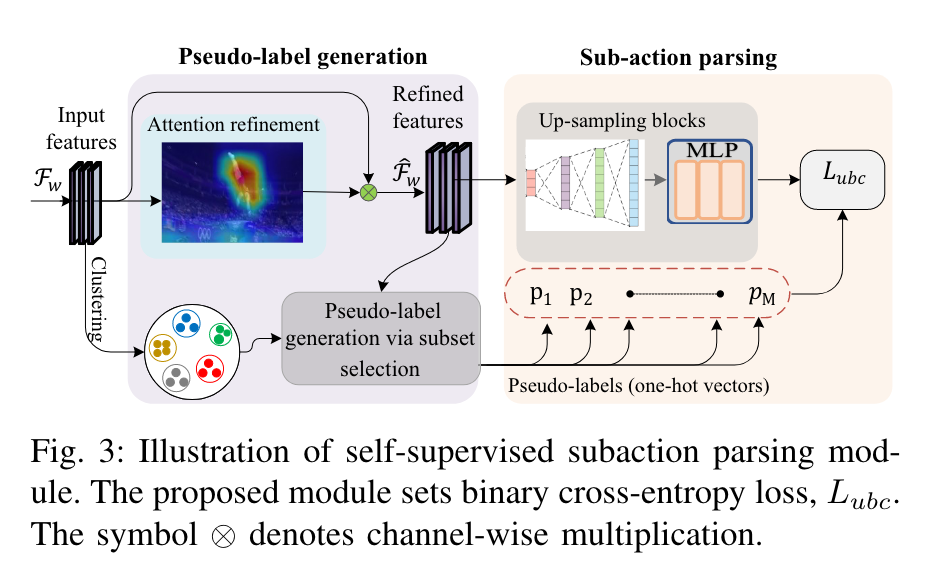
使用子集选择来构建子动作解析的伪标签。使用$\mathcal{F}_{w}^{t}$,$w \in \{u,a\}$表示$t$时刻的输入特征。
使用attention refinement(注意力优化或注意力精细化):引导选择视频帧中特征最多的的区域:全局平均池化(GAP)每个通道,输入特征映射减少到 C × 1 × 1 向量,捕获每个通道内的整体信息。sigmoid激活函数,计算通道范围的通道注意力分数,选择分数最高的通道(通道级注意力),特征减少之后怎么卷积。
然后进行逐通道乘法:(对特征进行通道放缩),结果是$\hat{F}_w^t$,增强了子动作集之间的特征差异。
伪标签生成:利用注意力特征和(潜在状态簇)clusters of latent states:先选择潜在状态簇集合,把他们作为子动作训练。然后将所有视频帧分配到这些子动作集中,子集选择过程将生成伪标签。
潜在状态簇$S$生成方法:k-means algorithm(k均值算法),$M$个中心,输入为$\mathcal{F}_{w}^{t}$,基于聚类选择子集的过程涉及使用集合 $S$ 内的状态 $M$ 以及子集选择组件中的注意力优化特征 $\hat{F}_w^t$。
生成潜在特征$S=\{s_1,s_2,\cdots,s_M\}$,表示输入特征中的不同模式或聚类。
聚类集合选择公式定义为:
$
\begin{aligned}
Z(\hat{\mathcal{S}})\triangleq\frac1T\sum_{t=1}^T\min_{i=\{1,\cdots,M\}}\|\hat{\mathcal{F}}_w^t-s_i\|_2
\end{aligned}
$
$Z(\hat{\mathcal{S}})$:最小化目标函数,时间序列上每一帧到最近的聚类中心的欧氏距离(L2范数)
输出包含$\hat{K}$个选择状态,对应子动作序列,$\hat{K}$小于等于$M$,不一定每个子动作模式或阶段都重要,$M$代表动作序列的细粒度。
因为假设有$K$个子动作集
贪心算法优化过程:初始化$\Gamma$为空,迭代添加状态从$S$到$\Gamma$,选择$\Gamma$中已有元素是的损失函数最小的状态。继续这个过程直到获取最多$\hat{K}$个状态。表示为$P=\{p_1,p_2,\cdots,p_M\}$,就是接下来要用的伪标签。
$P$集合有k个状态? (one-hot vectors (0-1向量))

输入:
所有可能的状态集合:$ \{1, \cdots, \hat{K}\} $和输入特征 $\hat{\mathcal{F}}_w^t $,这些特征来自视频的每一帧。
所有可能状态集合有$M$个
损失函数: $Z(\Gamma)$ 表示目标函数的值,所有帧与状态集合$\Gamma$的差异。
状态集合与每一帧的最小差异
增益函数:$ \delta{\Gamma}(z^) = Z(\Gamma) - Z(\Gamma \cup \{(z^)\}) $,表示将状态$ z^* $包含到当前选定状态集$ \Gamma$ 后,损失函数的减少量。
增加了一个状态后,差异会缩小,因为中心点多了。
增益函数为负值时,说明序列中的子动作小于$K$个。
输出:
最多选择 $\hat{K}$ 个状态作为子动作序列的伪标签。
步骤:
初始化活跃集:将活跃集 $\Gamma$ 设为空集。
迭代选择状态(共 $\hat{K}$ 次):
在每次迭代中,从所有状态中选择一个当前不在$ \Gamma$ 中的状态 $z^*$ ,使得添加该状态后目标函数的值减少最多。
贪心算法
计算加入状态 $z^$ 后的增益 $\delta_{\Gamma}(z^) $。
可能存在子动作数小于$K$
将状态 $z^*$ 添加到活跃集 $\Gamma $中。
返回结果:最终的活跃集 $\Gamma$ 中包含最多 $\hat{K}$ 个状态,这些状态作为子动作解析中的伪标签。
? 伪标签不带时间顺序吗?
二. subaction parsing:
- $M$ 是初始聚类生成的状态数,表示动作序列中的所有潜在子动作模式。
- $K$ 是通过子集选择算法从 $M $个状态中挑选出的最重要的$ K$ 个状态,用于伪标签生成和最终子动作的解析。
- 在子动作解析模块中,模型仍然输入的是 $M$ 个状态,因为需要完整的潜在状态来进行解析,最终再聚焦于$ K $个关键状态
每一帧生成一个M维的one-hot向量(0-1),代表可能的状态。每个子块在时间维度上扩展注意力优化特征,应用最大池化减少空间特征。MLP (多层感知器)投影到概率向量中,得到:$\begin{aligned}\mathcal{A}=\{a_1,\cdots,a_M\}\end{aligned}$,表示发生子动作的可能性。
投影公式为:$[a_1,\cdots,a_M]=\mathbb{F}_\emptyset(\hat{\mathcal{F}}_w^t)$
整体变为TxM的向量。 转置了
$\mathbb{F}$表示$\emptyset$参数下的自监督子动作解析
$a_M\in\mathbb{R}^T$是第 M 个潜在状态的预测概率。
T维向量,转置了
$\begin{aligned}
\bar{t}_k=\operatorname*{argmax}_{\frac TM(k-1)\leq t\leq\frac TMk}a_M(t)
\end{aligned}$
argmax, 返回最大值索引
两个连续的帧,即t和t + 1具有不同的表示。在此之后,动作解析在第(t + 1)帧标记新的子动作实例的开始。
$M$个时间段内,每个$t$的最大概率实例,表示为这个段内的实例。子动作划分是否具有细粒度?
其中:$p_M(t)$表示第$t$帧的伪标签的真实值。$a_M(t)$表示第$t$帧的预测概率分布。第$M^{th}$个序列的预测值是$\bar{t}_M$,充当给定序列的最好表示。
为了确保伪标签和$a_M(t)$ 预测的子动作解析之间的一致性,我们制定了二元交叉熵损失$L_{ubc}$,实现细粒度的高级内部结构及其时间依赖性。
$\begin{aligned}L_{ubc}&=-\sum_tp_M(t)\log_M(t)+(1-p_M(t))\log(1-a_M(t))\end{aligned}$
D. Group contrastive learning
组对比学习,实现相同语义间差异最小化,不同语义子集间差异最大化。
MLP projection head, 时空全局均值化。
$h_u=h_\varphi(\bar{\mathcal{F}}_u)$,$h_a=h_\varphi(\bar{\mathcal{F}}_a)$
然后,为这些输入的子动作概率分布向量分配与具有最大激活和高语义相似度的类相对应的伪标签。具有语义相似伪标签的特征以小批量的形式分组在一起,
$G_w^p=\frac{\sum_{i=1}^B1_{\{p=h_w\}}\mathrm{g}(h_w)}{T_B}$
相同语义对:$(G_a^p,G_u^p)$
不同语义对:$(G_a^p,G_u^q)$
组对比学习损失:
$L_{gc}=-\log\frac{\mathcal{H}(G_a^p,G_u^p)/\iota}{\mathcal{H}(G_a^p,G_u^p)/\iota+\sum_{q=1,k}^S\mathbb{1}_{p\neq q}\mathcal{H}(G_a^p,G_w^q)/\iota}$
损失函数
回归损失:$\bar{y}_i=\mathcal{R}_\vartheta\left(\bar{\mathcal{F}}_\ell\right)$
MSE(均方误差)损失:$L_{reg}=\frac1{\mathbb{N}_\ell}\sum_{i=1}^{\mathbb{N}_\ell}\left(\bar{y}_i-y_i\right)^2$
总损失:$L_{all}=L_{reg}+\lambda_1L_{ubc}+\lambda_2L_{un}+\lambda_3L_{gc}$
其中$\lambda_1$:超参数
实验
数据集和参数
数据集
MTL-AQA:
FineDiving:
Rhythmic Gymnastics
FineFS
参数
评价指标(斯皮尔曼系数):$\rho=\frac{\sum_i(y_i-y)(\bar{y}_i-\bar{y})}{\sqrt{\sum_i(y_i-y)^2\sum_i(\bar{y}_i-\bar{y})^2}}$
消融实验 Ablation Study
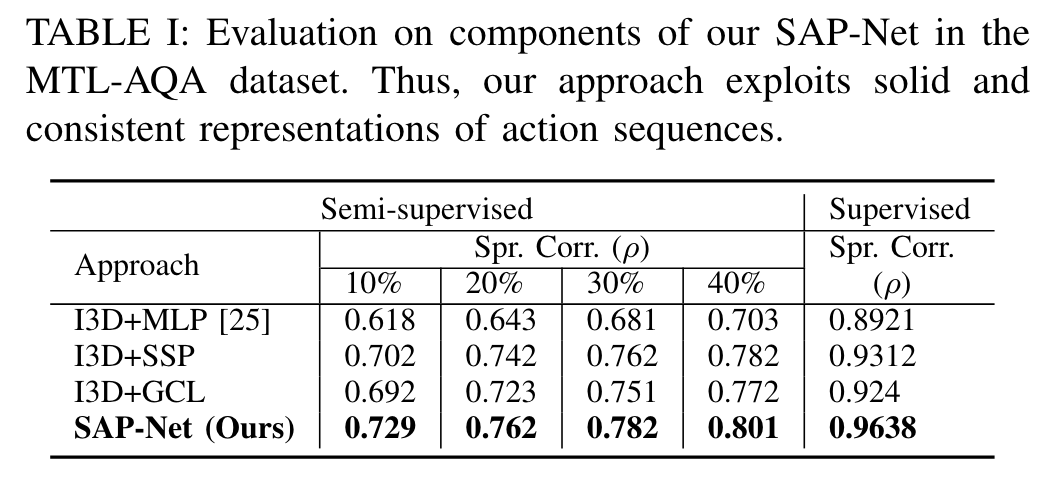
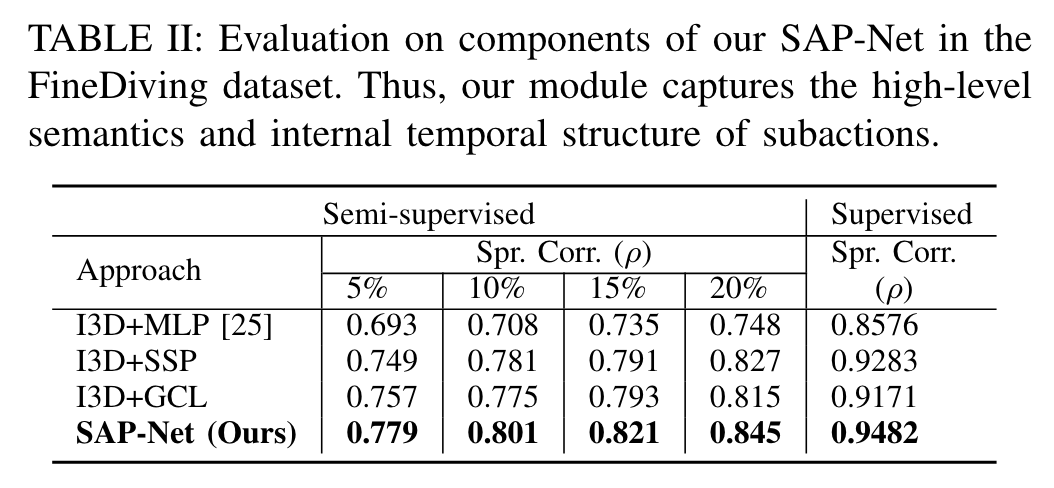
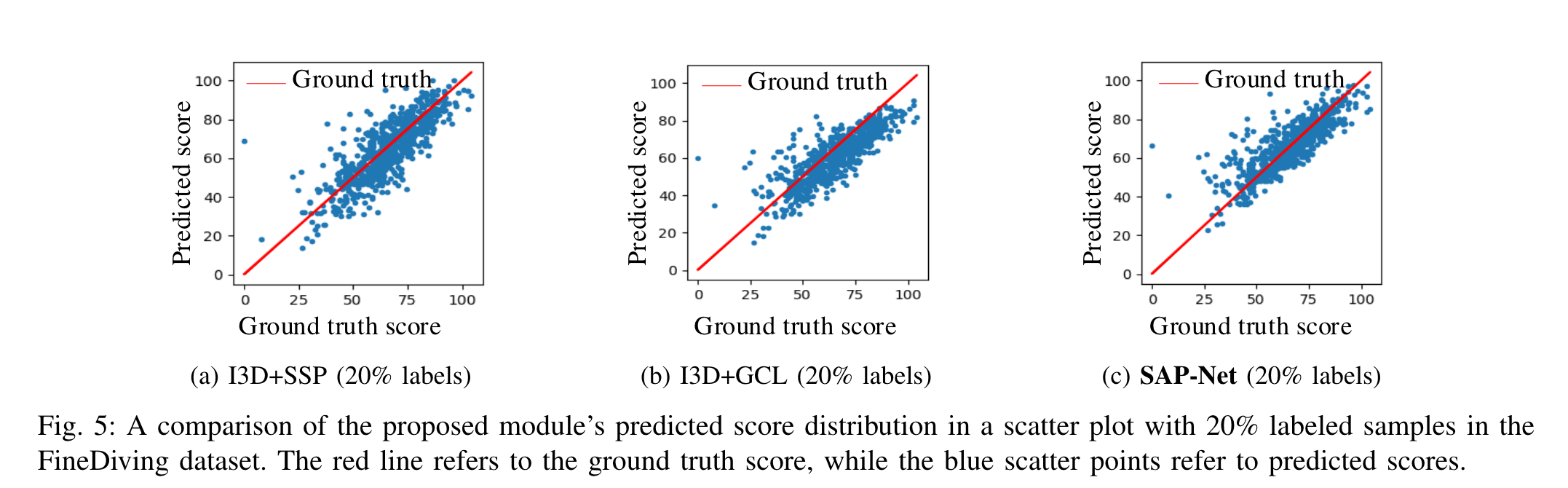
预测值和真实值的可视化分布:
对标记样本比例的敏感性:
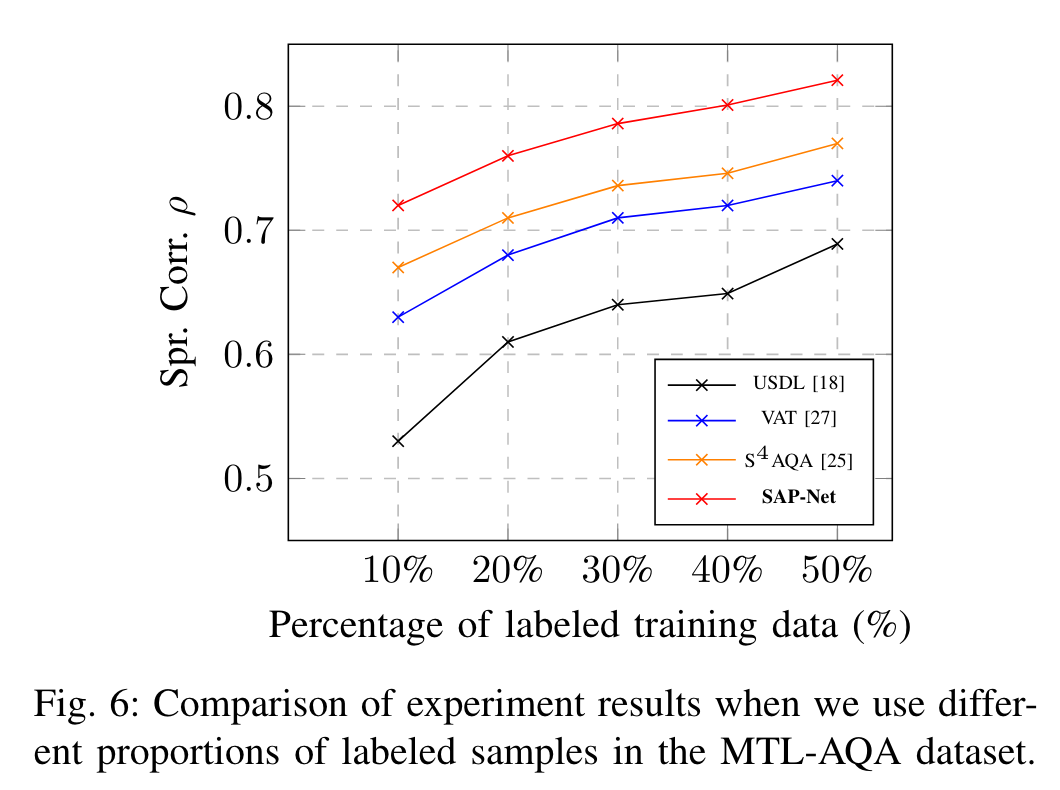
10%的标记数据达到了$S^4AQA$的40%标记样本的效果。
阈值的影响:FineDiving-15%
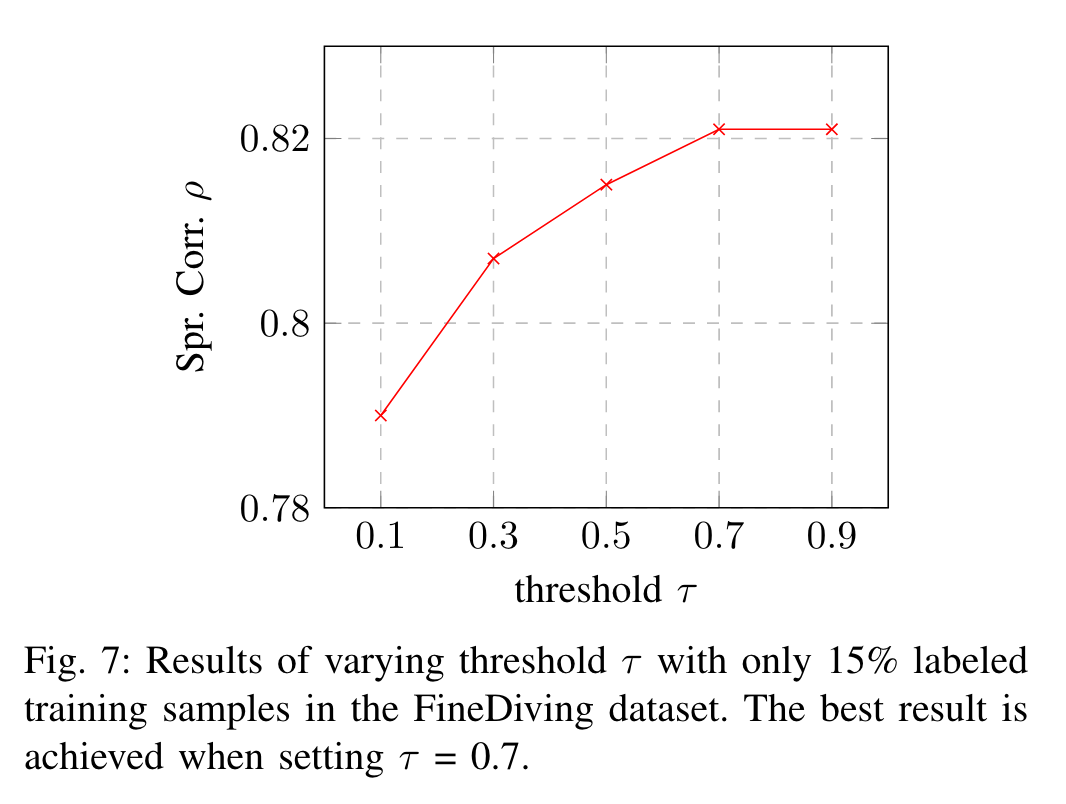
损失函数的评估:
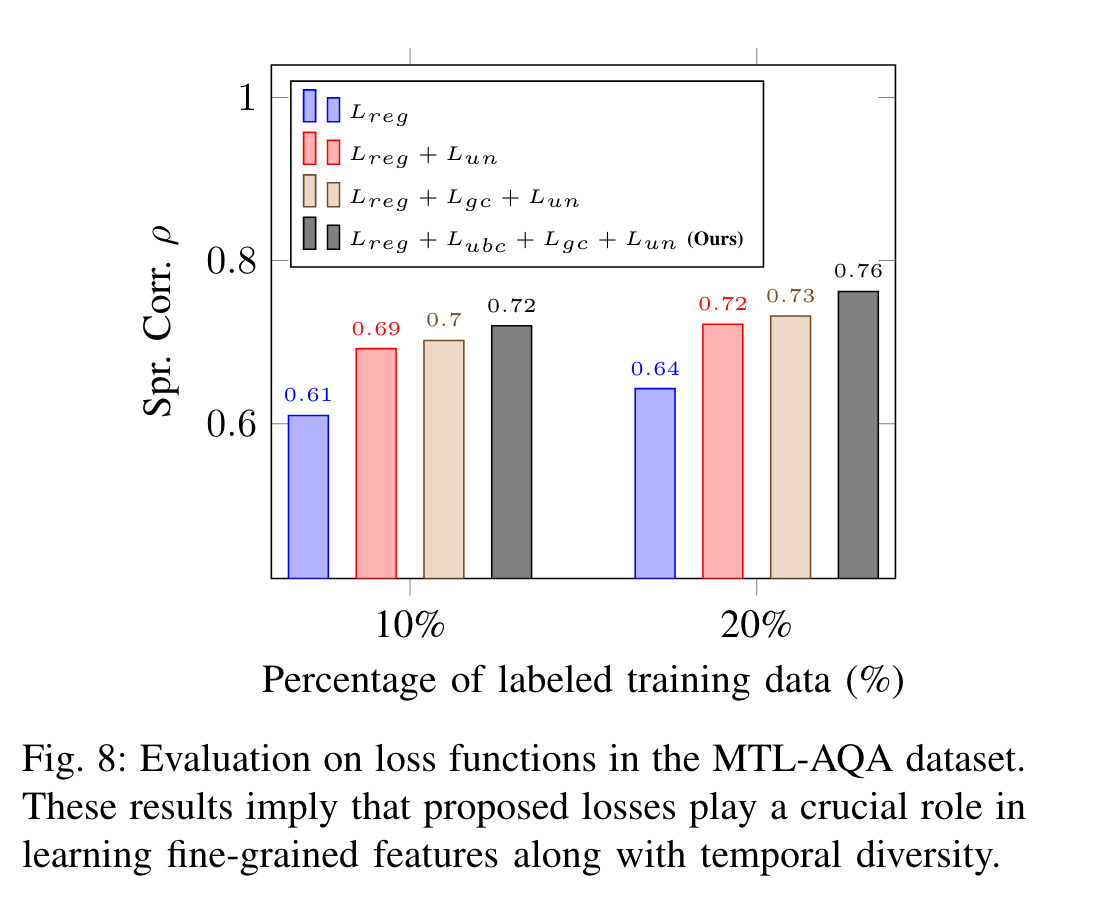
作者认为:$L_{gc}$和$L_{ubc}$在学习具有时间多样性的细粒度特征方面起着至关重要的作用。
对最优子动作数量$K$的评价:
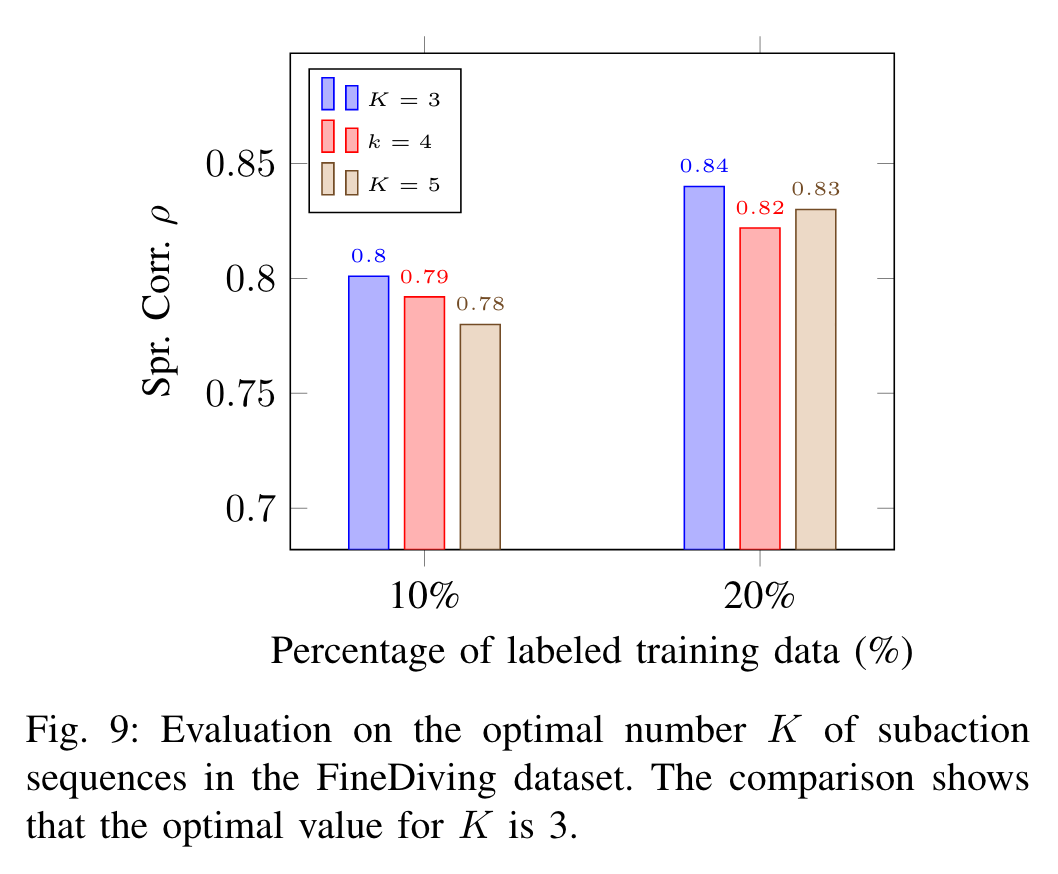
跳水三个阶段。
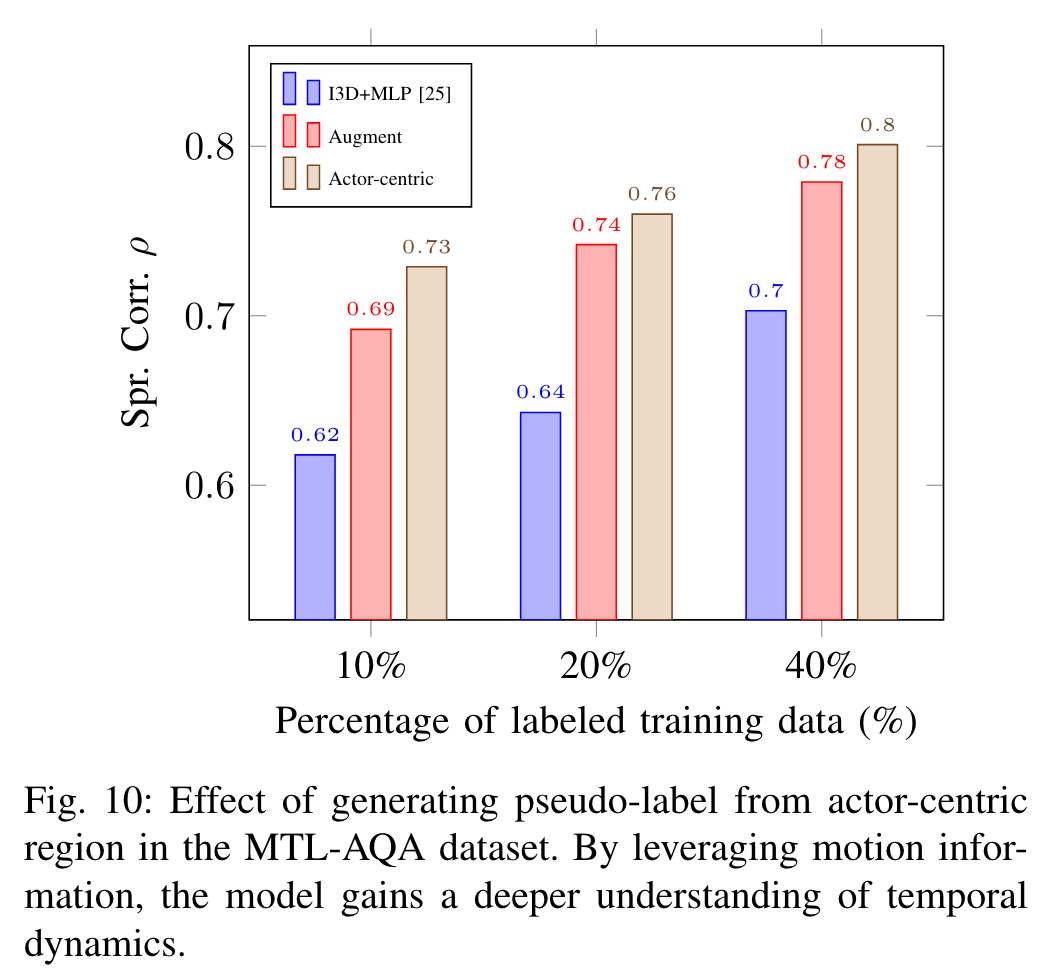
伪标签的演员中心区域:
替换为一个增强版本,在保持视频语义不变的情况下,从输入剪辑中改变像素级别的分布。
应该是手动剪辑的意思
注意力细化对子动作解析的影响:
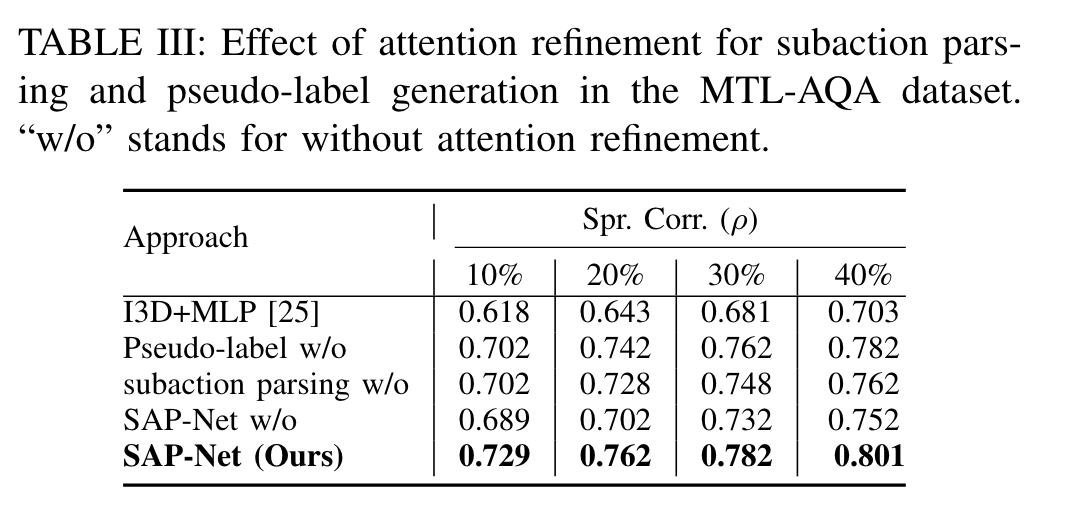
w/o,没有注意力细化
与最先进的方法对比
每个数据集上最先进的方法:
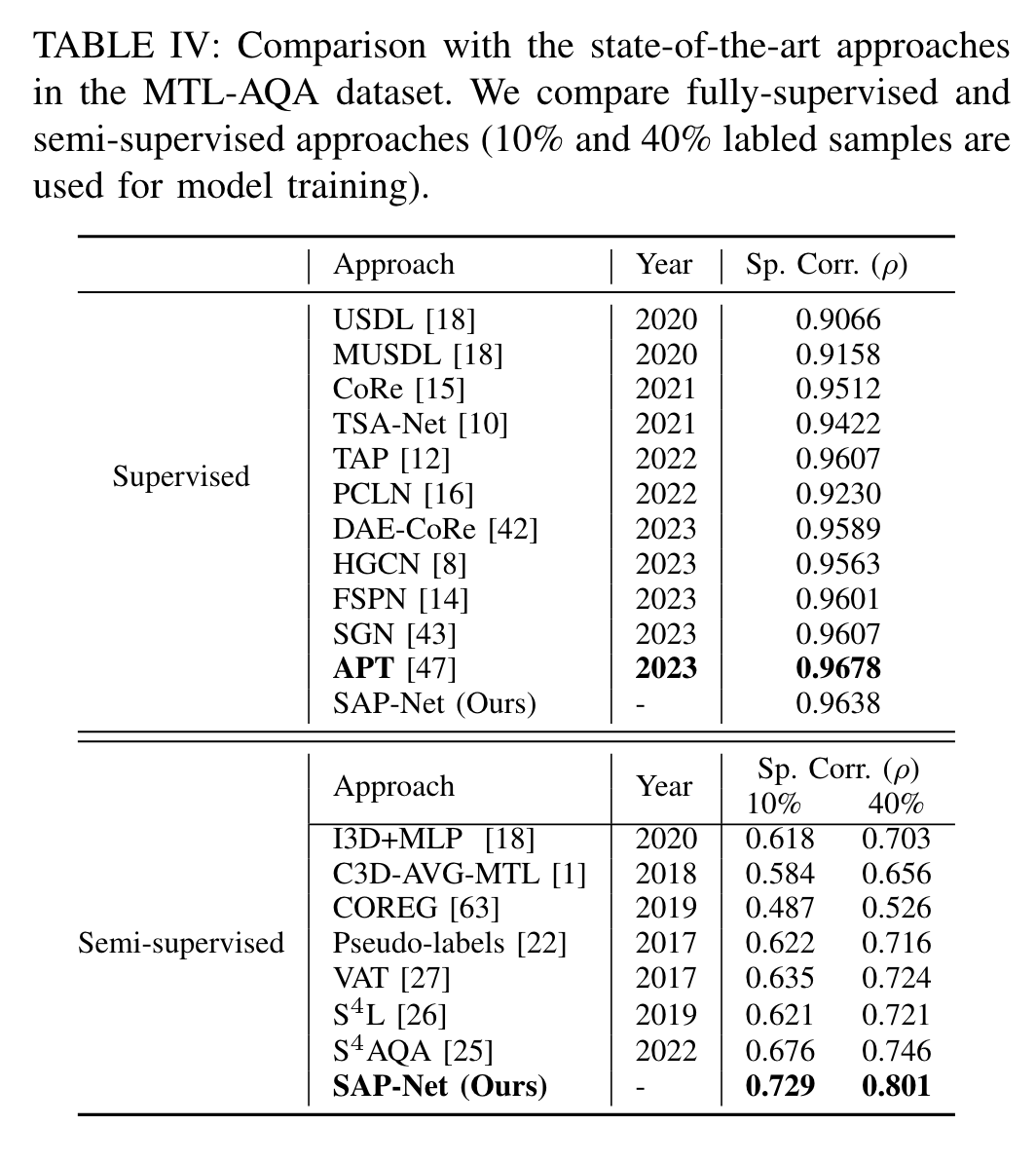
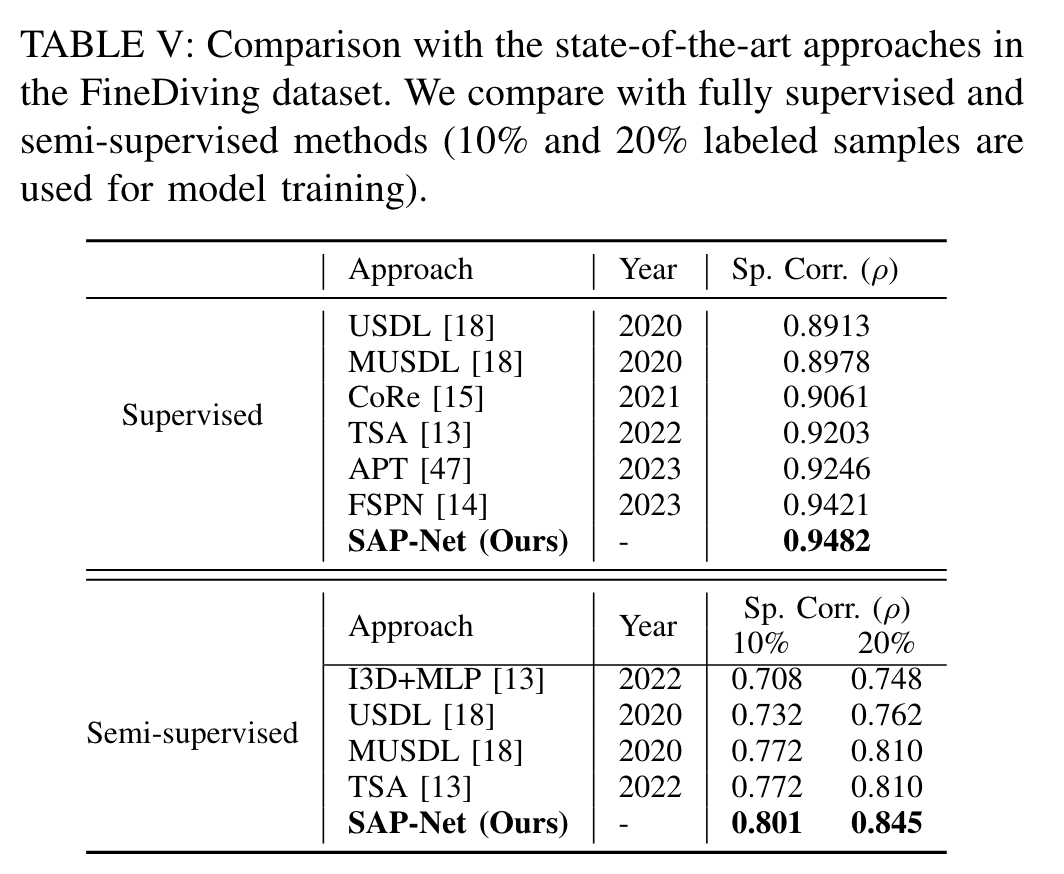
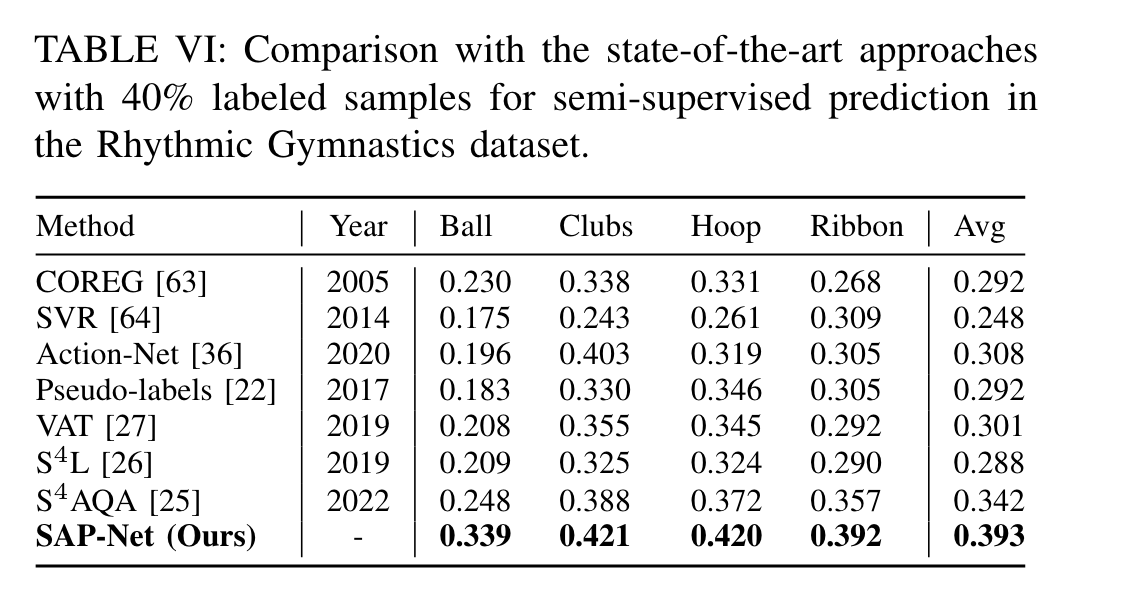
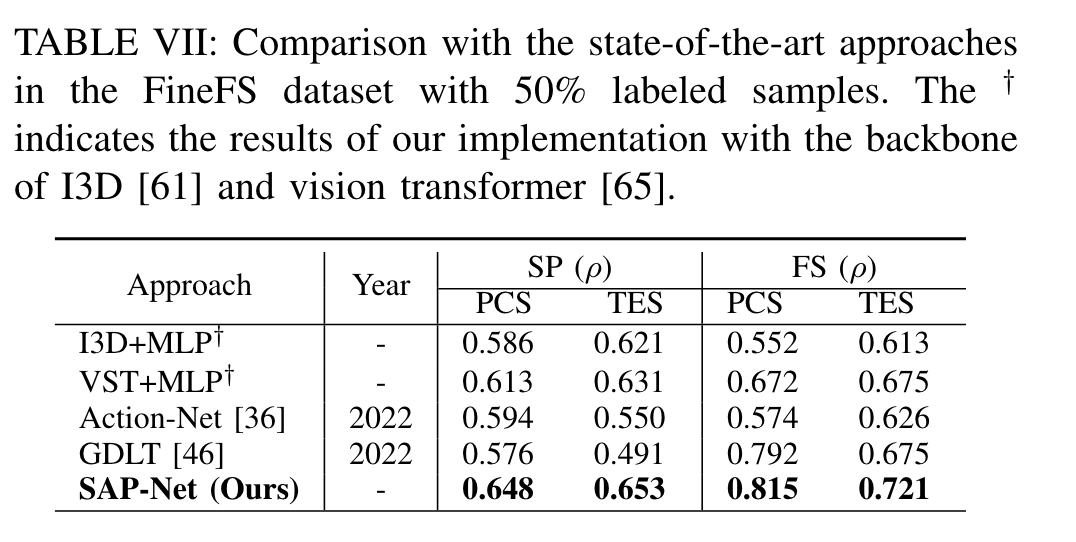
可视化结果
注意力细化和演员中心的效果:

不同比例标记的散点图:
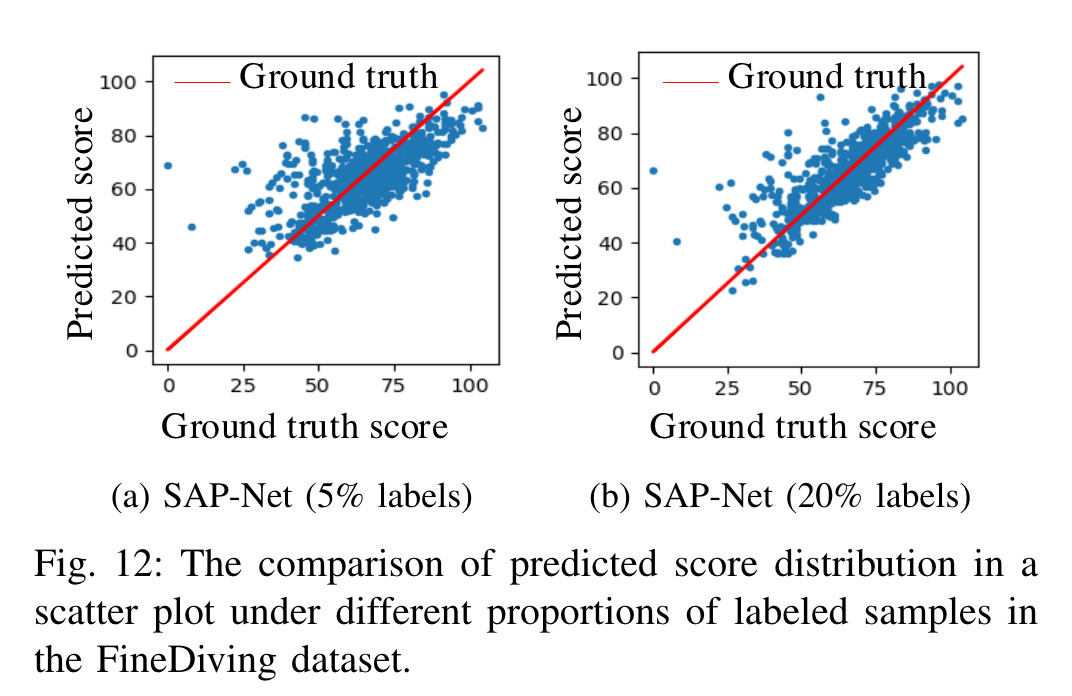
失败样本:
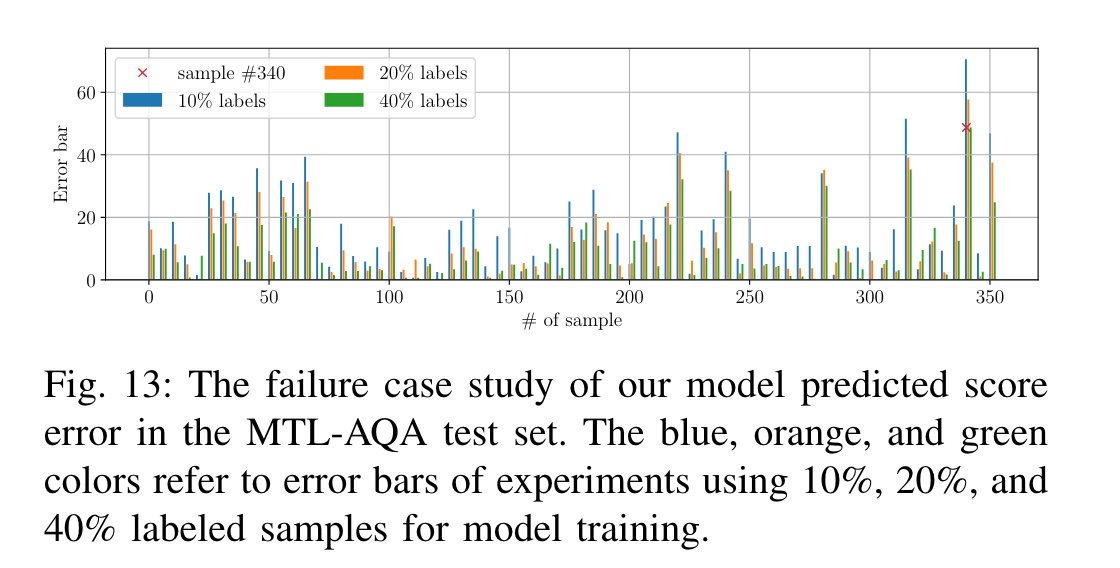

误差较大的样本340,动作失误,被判0分。
动作犯规后,评分不线性,0分