经典卷积神经网络-ResNet
卷积神经网络
卷积层前向传播
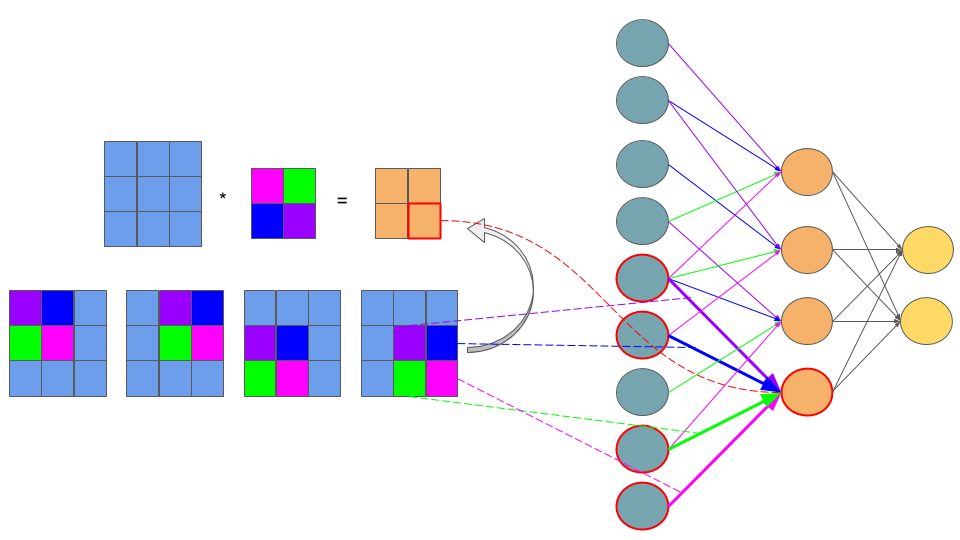
梯度反向传播的卷积
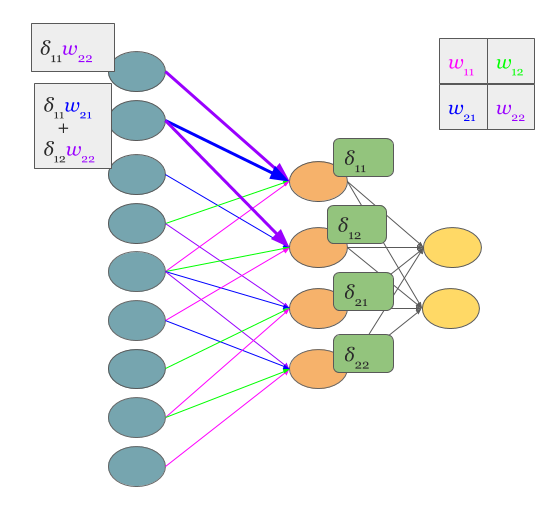
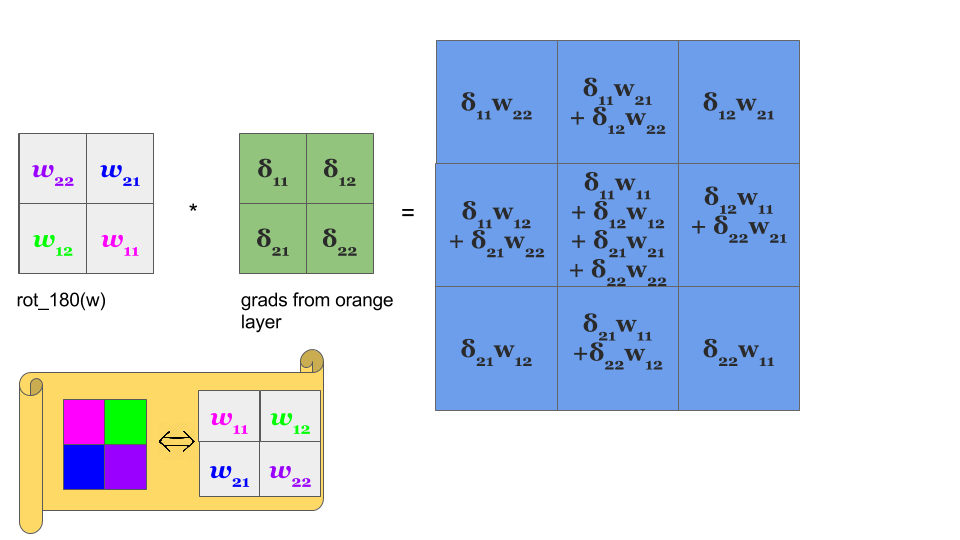
反向传播使用了这种卷积操作,将权值矩阵旋转180度,而梯度矩阵会进行填充为:
$\left.\left[\begin{array}{llll}\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\delta_{11}^l&\delta_{12}^l&\mathbf{0}\\\mathbf{0}&\delta_{21}^l&\delta_{22}^l&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{0}\end{array}\right.\right]$
下图是反向传播的更新梯度,(图片没有填充):
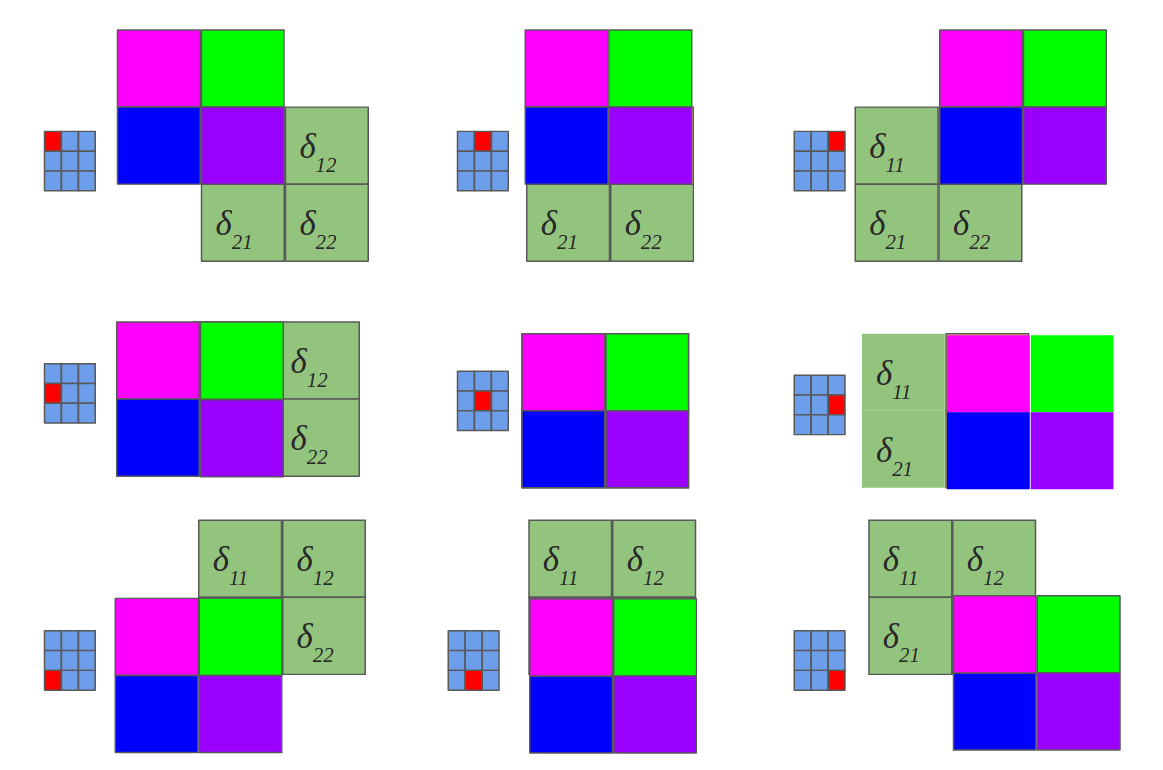
卷积将卷积核旋转180度,然后进行互相关操作。
二维卷积公式
深度学习中的卷积是先旋转180度,然后互相关操作。
前馈神经网络中:神经元$j$的误差定义为:
$\delta_j^l=\frac{\partial C}{\partial z_j^l}$
其中:$z_j^l=\sum_kw_{kj}^la_k^{l-1}+b_k^l$
$a_j^l=\sigma(z_j^l)$,激活函数
其中$w_{kj}^l$:是第$l-1$与$l$层之间的输入$k$节点与输出$j$节点的权重,
对于CNN:
前向传播公式为:
$
\begin{aligned}
z_{x,y}^{l+1} = w^{l+1}*\sigma(z_{x,y}^l)+b_{x,y}^{l+1} = \sum_{a}\sum_{b}w_{a,b}^{l+1}\sigma(z_{x-a,y-b}^l) +b_{x,y}^{l+1}
\end{aligned}
$
其中$z_{x-a,y-b}^l$:相当于对核翻转。
定义误差梯度:
$\begin{aligned}\delta_{x,y}^l=\frac{\partial C}{\partial z_{x,y}^l}=\sum_{x^{\prime}}\sum_{y^{\prime}}\frac{\partial C}{\partial z_{x^{\prime},y^{\prime}}^{l+1}}\frac{\partial z_{x^{\prime},y^{\prime}}^{l+1}}{\partial z_{x,y}^l}\end{aligned}$
其中$x^{\prime},y^{\prime}$,取决于前向传播卷积的示意图中,$l$层每个节点$x,y$,影响的$l+1$层的$x^{\prime},y^{\prime}$不同。
将前向传播带入公式:
$\begin{aligned}
\frac{\partial C}{\partial z_{x,y}^l} & =\sum_{x^{\prime}}\sum_{y^{\prime}}\frac{\partial C}{\partial z_{x^{\prime},y^{\prime}}^{l+1}}\frac{\partial z_{x^{\prime},y^{\prime}}^{l+1}}{\partial z_{x,y}^{l}} \\
&=\sum_{x^{\prime} }\sum_{y^{\prime}}\delta_{x^{\prime},y^{\prime} }^{l+1}\frac{\partial(\displaystyle\sum_{a}\displaystyle\sum_{b}w_{a,b}^{l+1}\sigma(z_{x^{\prime}-a,y^{\prime}-b}^{l})+b_{x^{\prime},y^{\prime}}^{l+1}) }{\partial z_{x,y}^{l}}
\end{aligned}$
对公式右边进行展开,只有$x = x^{\prime} - a$和$y = y^{\prime} -b$时偏导不为0,故重新整理后得,将$a = x^{\prime} - x$和$b = y^{\prime} -y$代入:
$\begin{aligned}\sum_{x’}\sum_{y’}\delta_{x’,y’}^{l+1}w_{a,b}^{l+1}\sigma’(z_{x,y}^l)&=\sum_{x’}\sum_{y’}\delta_{x’,y’}^{l+1}w_{x’-x,y’-y}^{l+1}\sigma’(z_{x,y}^l)\end{aligned}$
上述式子中:$x’-x$不会超出范围,因为$x’$与$x$具有关联,所以一定会在$w$的矩阵范围内。
而右边第一项就是梯度反向传播的公式:
$\begin{aligned}\delta^{l+1}*w_{-x,-y}^{l+1} = \sum_{x’}\sum_{y’}\delta_{x’,y’}^{l+1}w_{x’-x,y’-y}^{l+1}\end{aligned}$
理解上面这个公式:

$\delta_{1,2}^{l}$,只影响了下一层的$\delta_{1,1}^{l+1}$$\delta_{1,2}^{l+1}$,所以$x’,y’$取值范围只有$(1,1),(1,2)$,得到的$w$下标${x’-x,y’-y}$,取值为:$(0,-1),(0,0)$
推导公式:
所以最终的反向传播误差公式:
$\delta_{x,y}^l=\delta^{l+1}*ROT180(w_{x,y}^{l+1})\sigma^{\prime}(z_{x,y}^l)$
成本函数的梯度:
$\frac{\partial C}{\partial w_{a,b}^l}=\delta_{a,b}^l*\sigma(ROT180(z_{a,b}^{l-1}))$
链接
Derivation of Backpropagation in Convolutional Neural Network (CNN)
Derivation of Backpropagation in Convolutional Neural Network zhangzhifei.pdf)
基础知识
矩阵微分
矩阵:$f(\boldsymbol{X}),\boldsymbol{X}_{m\times n}=(x_{ij})_{i=1,j=1}^{m,n}$
多元函数设为可微:
$
\begin{aligned}
\mathrm{d}f(\boldsymbol{X})& =\frac{\partial f}{\partial x_{11}}\mathrm{d}x_{11}+\frac{\partial f}{\partial x_{12}}\mathrm{d}x_{12}+\cdots+\frac{\partial f}{\partial x_{1n}}\mathrm{d}x_{1n} \\
&+\frac{\partial f}{\partial x_{21}}\mathrm{d}x_{21}+\frac{\partial f}{\partial x_{22}}\mathrm{d}x_{22}+\cdots+\frac{\partial f}{\partial x_{2n}}\mathrm{d}x_{2n} \\
&+\ldots \\
&+\frac{\partial f}{\partial x_{m1}}\mathrm{d}x_{m1}+\frac{\partial f}{\partial x_{m2}}\mathrm{d}x_{m2}+\cdots+\frac{\partial f}{\partial x_{mn}}\mathrm{d}x_{mn}
\end{aligned}
$
相当于:
$
\begin{aligned}
\mathrm{d}f(\boldsymbol{X})=\mathrm{tr}(\begin{bmatrix}\frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{21}}&\cdots&\frac{\partial f}{\partial x_{m1}}\\\frac{\partial f}{\partial x_{12}}&\frac{\partial f}{\partial x_{22}}&\cdots&\frac{\partial f}{\partial x_{m2}}\\\vdots&\vdots&\vdots&\vdots\\\frac{\partial f}{\partial x_{1n}}&\frac{\partial f}{\partial x_{2n}}&\cdots&\frac{\partial f}{\partial x_{mn}}\end{bmatrix}_{n\times m}\begin{bmatrix}\mathrm{d}x_{11}&\mathrm{d}x_{12}&\cdots&\mathrm{d}x_{1n}\\\mathrm{d}x_{21}&\mathrm{d}x_{22}&\cdots&\mathrm{d}x_{2n}\\\vdots&\vdots&\vdots&\vdots\\\mathrm{d}x_{m1}&\mathrm{d}x_{m2}&\cdots&\mathrm{d}x_{mn}\end{bmatrix}_{m\times n})
\end{aligned}
$
Jacobian矩阵形式:
即先把矩阵变元$X$进行转置,再对转置后的每个位置的元素逐个求偏导,结果布局和转置布局一样
$
\begin{aligned}
\operatorname{D}_\boldsymbol{X}f(\boldsymbol{X})& =\frac{\partial f(\boldsymbol{X})}{\partial\boldsymbol{X}_{\boldsymbol{m}\times\boldsymbol{n}}^T} \\
&=\begin{bmatrix}\frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{21}}&\cdots&\frac{\partial f}{\partial x_{m1}}\\\frac{\partial f}{\partial x_{12}}&\frac{\partial f}{\partial x_{22}}&\cdots&\frac{\partial f}{\partial x_{m2}}\\\vdots&\vdots&\vdots&\vdots\\\frac{\partial f}{\partial x_{1n}}&\frac{\partial f}{\partial x_{2n}}&\cdots&\frac{\partial f}{\partial x_{mn}}\end{bmatrix}_{n\times m}
\end{aligned}
$
$\boldsymbol{X}_{m\times n}$的矩阵微分:
$
\begin{aligned}\mathrm{d}\boldsymbol{X}_{m\times n}=\begin{bmatrix}\mathrm{d}x_{11}&\mathrm{d}x_{12}&\cdots&\mathrm{d}x_{1n}\\\mathrm{d}x_{21}&\mathrm{d}x_{22}&\cdots&\mathrm{d}x_{2n}\\\vdots&\vdots&\vdots&\vdots\\\mathrm{d}x_{m1}&\mathrm{d}x_{m2}&\cdots&\mathrm{d}x_{mn}\end{bmatrix}_{m\times n}\end{aligned}
$
于是,矩阵微分形式为:
$
\begin{aligned}\mathrm{d}f(\boldsymbol{X})=\mathrm{tr}(\frac{\partial f(\boldsymbol{X})}{\partial\boldsymbol{X}^T}\mathrm{d}\boldsymbol{X})
\end{aligned}
$