ST-GCN 时空图卷积神经网路

发表于 2024-09-13 更新于 2024-11-01 分类于论文阅读阅读次数：

STGCN是一种时空图卷积网络,通过将图神经网络扩展到时空图模型。设计一种用于动作识别的骨架序列的通用表示，称为时空图卷积神经网络。

论文名称：Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition

论文笔记

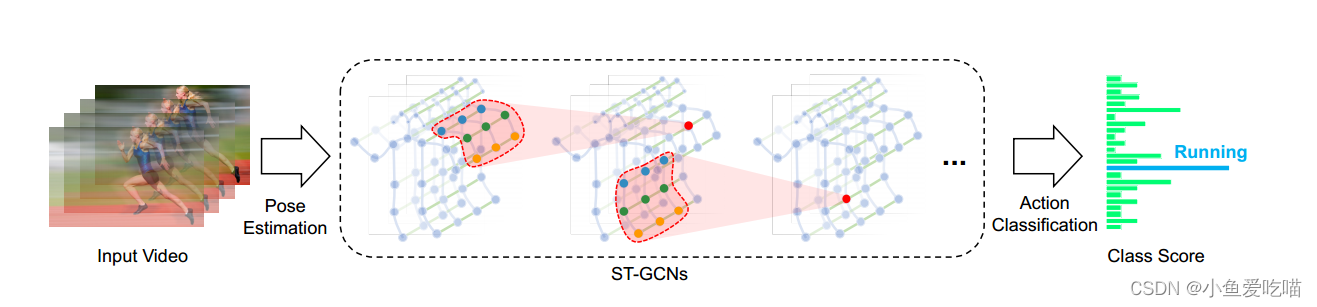
在这里插入图片描述

对视频进行姿态估计，在骨架序列上构造时空图；
在输入数据上应用多层时空图卷积(ST-GCN)，逐步在图上生成更高层次的特征图；
然后由标准 Softmax 分类器将其分类到相应的动作类别。
整个模型采用反向传播的端到端方式训练。

摘要

传统的骨骼建模方法依赖于手工制作的部件或遍历规则，表达能力有限和泛化困难，模型很难推广到其他应用。
这项工作提出了动态骨架模型。

主要内容

提出了 ST-GCN，这是一种基于图的动态骨骼建模通用公式，这是第一个将基于图的神经网络应用于该任务。
针对骨架建模的具体要求，提出了 ST-GCN 中卷积核的设计原则。
在基于骨骼的动作识别的两个大规模数据集上，与之前使用手工制作部件或遍历规则的方法相比，所提出的模型获得了更好的性能，在手工设计方面的工作量大大减少。ST-GCN 的代码和模型是公开的。

ST-GCN：基于图的动态骨骼建模通用公式

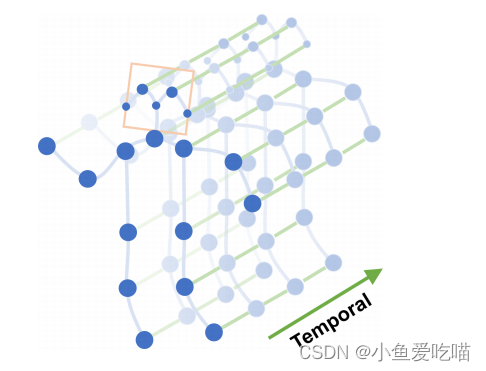
分别为两种边：时间边，空间边。
ST-GCN 的层次特性消除了手工制作的部件分配或遍历规则的需要。

传统的骨架模型方法中，根据预定义的部件分配和遍历规则对骨架进行建模。
具体规则：
1.人体骨架的构成方式和连接顺序。
2.节点对应的身体部位、编号和名称等信息。
3.骨架节点的搜索顺序和遍历方式。

STGCN可以动态学习现有数据的关系规则

ST-GCN 在进行时空图卷积之前，仍然需要对骨架节点进行部件分配和遍历规则的设计。可以根据不同任务，设定不同规则。

ST-GCN 模型中的组件

在具有 N 个关节和 T 个框架（帧）的骨架序列上构造了无向时空图 $G=(V,E)$

节点集$V=\{v_{ti}\left|t=1, \ldots, T;i=1, \ldots, N\right\}$包括骨架序列中的所有关节,节点 $F(v_{ti}\mathrm{~})$ 上的特征向量由帧 $t$ 上第 $i$ 个关节的坐标向量和估计置信度组成。
边集 E:
骨架内连接，记为 $E_S=\{v_{ti} v_{tj} |(i,j)\in H\},$，其中 $H$ 为自然连接的人体关节集合
帧间边：$E_F=\{v_{ti}v_{(t+1)i}\}$

空间图卷积神经网络

单帧的图CNN模型

在时间 $\tau$ 的单个帧上，将有 $N$ 个关节节点 $V_t$，以及骨架边 $E_S\left(\tau\right)=\{v_{ti} v_{tj} |t=\tau , (i,j)\in H\}$。

给定核尺寸为 $K×K$ 的卷积算子，以及通道数量为 $c$ 的输入特征映射 $f_{in}$。在空间位置 $x$ 处，单个通道的输出值可以写成：
$f_{out}\left(x\right)=\sum_{h=1}^K\sum_{w=1}^Kf_{in}\left(\mathbf{p}(\mathbf{x},h,w)\right)\cdotp\mathbf{w}(h,w)$

抽样函数 $\mathbf{p}$：$Z^2\times Z^2\to Z^2$ 列举了空间位置 $x$ 的邻居的位置。在图像卷积，它也可以表示为 $\mathbf{p}(\mathbf{x},h,w)=\mathbf{x}+\mathbf{p}^{\prime}(h,w)$。权函数 $\mathbf{w}$:$Z^2\to\mathbb{R}^c$ 提供了一个 $c$ 维实空间中的权向量，用于计算与采样的 $c$ 维输入特征向量的内积。注意，权函数与输入位置 $x$ 无关。因此，在输入图像滤波器权重到处都是共享的。

$\mathbf{p}^{\prime}(h,w)$：映射一个方向访问函数，类似象棋中的[0,-1],[1,0];

抽样函数 $\mathbf{p}$：就是一个编码的定位函数，映射$x$位置附近的卷积核内对应的位置。

从二维抽象到三维：
通过将上述公式扩展到输入特征映射位于空间图 $V_t$ 上的情况，来定义图上的卷积操作。即特征映射 $f_{in}^t$：$V_t→R^c$ 在图的每个节点上都有一个向量。扩展的下一步是重新定义抽样函数 p 和权重函数 w。

采样函数

在图像上，采样函数 $\mathbf{p}(h,w)$ 是在相邻像素点关于中心位置 $x$ 上定义的。在图上，我们同样可以在节点 $v_{ti}$ 的邻居集 $B(v_{ti})=\{v_{tj}|d(v_{tj},v_{ti})\leq D\}$ 上定义采样函数。这里 $d(v_{tj},v_{ti}\mathrm{~})$ 表示从 $v_{tj}$ 到 $v_{ti}$ 的任何路径的最小长度。因此，抽样函数 $\mathbf{p}:B(v_{ti})\to V$ 可以写成：
$\mathbf{p}(v_{ti},v_{tj})=v_{tj}$

注意这里的 $v_{tj}$ 是节点 $v_{ti}$ 的邻居集 $B(v_{ti})$ 中的节点，即当 $D=1$ 时，采样函数 $\mathbf{p}$ 取的是邻接点。

权重函数

主要是如何定义图的顺序，保证权重可以按顺序对邻接点作用。

将一个关节点 $v_{ti}$ 的邻居集 $B(v_{ti})$ 划分为固定数量的 $K$ 个子集，其中每个子集都有一个数字标签，从 $0$ 到 $K-1$。

映射 $l_{ti}: B(v_{ti} )\to\{0, \ldots, K-1\}$，
权重函数 $\mathbf{w}(v_{ti},v_{tj}):B(v_{ti})\to R^c$ 可以通过索引一个 $(c,K)$ 维张量或
$\mathbf{w}(v_{ti},v_{tj})=\mathbf{w}^{\prime}(l_{ti}\left(v_{tj}\right))$
来实现。

即相同标签会使用同一个权重，保持权重函数不变，拓展到每个节点。

c：指通道数

空间图卷积

有了改进的抽样函数和权函数，我们现在用图卷积重写公式(1)如下：
$f_{out}\left(v_{ti}\right)=\sum_{v_{tj}\in B(v_{ti})}\frac1{Z_{ti}\left(v_{tj}\right)}f_{in}\left(\mathbf{p}(v_{ti},v_{tj})\right)\cdotp\mathbf{w}(v_{ti},v_{tj})$其中归一项 $Z_{ti}\left(v_{tj}\right.)=\left|v_{tk}\left|l_{ti}\left(v_{tk}\right.\right)=l_{ti}\left(v_{tj}\right.\right)|$ 等于相应子集的基数。为了平衡不同子集对输出的贡献。

得到
$f_{out}\left(v_{ti}\right)=\sum_{v_{tj}\in B\left(v_{ti}\right)}\frac1{Z_{ti}\left(v_{tj}\right)}f_{in}\left(v_{tj}\right)\cdotp\mathbf{w}(l_{ti}\left(v_{tj}\right))$

时空建模

需要重新定义相邻位置的关系，增加时间相邻点。

将2D图像增加时间维度，转换为3D图像，应用到图卷积神经网络。

$B(v_{ti})=\{v_{qj}\left|d(v_{tj},v_{ti})\leq K,\left|q-t\right|\leq\left\lfloor\Gamma/2\right\rfloor\right\}$
该公式定义了每个节点的邻域 $B(v_{ti})$ 包括空间距离不超过 $K $个单位的所有节点和时间距离不超过 $\lfloor\Gamma/2\rfloor$ 个单位的所有节点。其中，参数 $\Gamma$ 控制时间上要包含在邻域图中的范围，因此可以称为时间内核大小。

重新修改映射标签：$l_{ST}\left(v_{qj}\right)=l_{ti}\left(v_{tj}\right)+\left(q-t+\left\lfloor\Gamma/2\right\rfloor\right)\times K$
其中 $l_{ti}\left(v_{tj}\right)$ 是在一个单帧 $t$ 上关节 $i$ 的邻接点 $j$ 的标签映射，而 $(q-t+\lfloor\Gamma/2\rfloor)\times K$ 用于在时间维度上对标签进行编码。

对时间的前后正负，转移到正数轴上，乘$K$，将所有的数据转移到一维数组内的顺序。可以通过每一个下标，定位到第几个节点的第几个时间帧内。

注：时间顺序(-1,0,1)，变换映射到(0,1,2)的三组K维标签上。

分区策略

标签映射：将相邻的接点映射到标签内。
标签划分：如何确定接点的属于哪个标签。

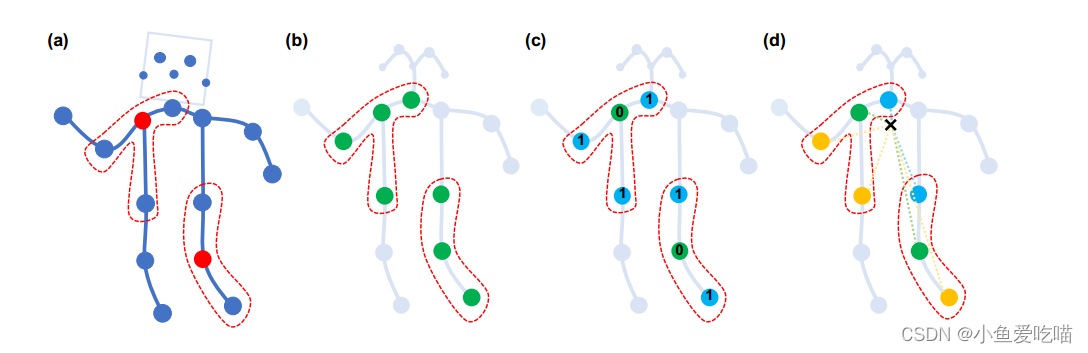
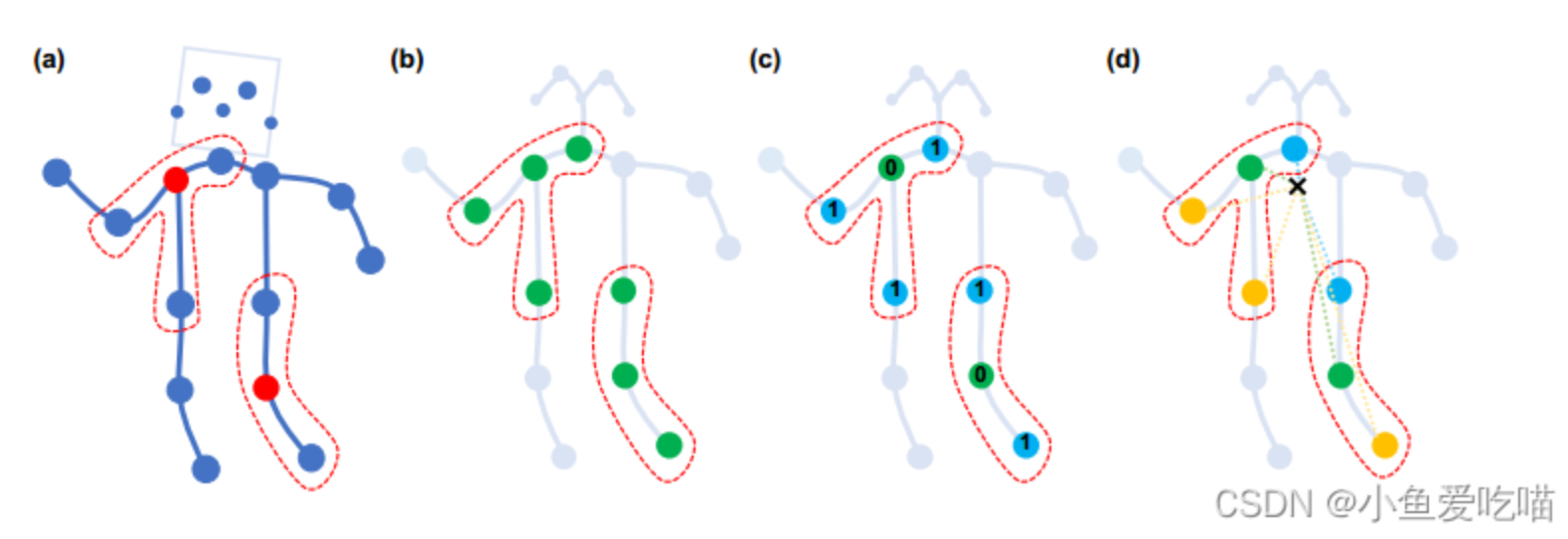
上图是构造卷积运算的划分策略。从左到右：

（a）输入骨架示例帧。身体关节用蓝点绘制。D=1 的过滤器的接受域用红色虚线圈绘制。

（b）单标签分区策略，即一个邻域内的所有节点都有相同的标签(绿色)。

（c）距离分区策略，这两个子集是距离为0的根节点本身(绿色)和距离为1的其他相邻点(蓝色)。

（d）空间结构分区策略，节点根据与骨架重心(黑色十字)的距离分为：根节点(绿色)的距离最近，向心节点的距离较短(蓝色)，而离心节点的距离较长(黄色)。

相同标签的子集，使用相同的权重。

Uni-labeling 单标签分区策略

所有节点一个标签，只有一种权重。

istance partitioning 距离分区策略

$D$ = 1,的情况下，只有两种权重，分为两个子集。

Spatial configuration partitioning 空间结构分区策略

将节点集分为三个子集： 只有一种连接划分，没有节点划分
1)根节点；距离中心节点最近的节点

2)近节点：距离跟第二近的节点

3)否则远连接。其他节点

将节点之间的连接分为三个子集：
1)根连接；如果两个节点与中心节点跳距相同，视为根连接
具有对称性

2)近连接：一个节点比另一个节点距离中心节点更近
j>i,则$adj[j][i]$属于近连接，看终点的距离

3)否则远连接。

$\begin{aligned}
l_{ti}\left(v_{tj}\right)=
\begin{cases}
0, & r_j=r_i \\
1, & r_j < r_i \\
2, & r_j > r_i
\end{cases}
\end{aligned}$

其中 $r_i$ 是训练集中所有帧中从重心到关节 $i$ 的平均距离。

会不会出现三种标签，只有两种：如端节点

可学习边缘重要性加权

我们在时空图卷积的每一层上都加上一个可学习的掩码 $M$。
掩码将根据 $E_s$ 中每个空间图边的学习重要性权重，将节点的特征贡献扩展到其邻近节点。

作者认为未来改进方向

也可以使用一个依赖于数据的注意力图，来提升空间特征的贡献扩展效果。

实现 ST-GCN

我们采用类似于(Kipf和Welling 2017)中的图卷积实现。单帧内关节的体内连接由表示自连接的邻接矩阵 $A$ 和单位矩阵 $I$ 表示。
在单帧情况下，采用第一个分区策略的 ST-GCN 可以用以下公式实现
$\mathbf{f}_{out}=\mathbf{\Lambda}^{ {-\frac{1}{2}} }(\mathbf{A}+\mathbf{I})\mathbf{\Lambda}^{ {-\frac{1}{2}} }\mathbf{f}_{in}\mathbf{W}$
解释：

$\mathbf{f}_{in}$: 输入特征矩阵,每行对应一个节点的特征向量,是一个行向量，具有多个特征。
$\mathbf{\Lambda}$: 度矩阵
$\mathbf{\Lambda}^{ {-\frac{1}{2}} }$: 平方根的倒数，用于归一化
$\mathbf{A}$: 邻接矩阵, 行$i$是出发点，列$j$是连接点
$\mathbf{I}$: 单位矩阵，表示自环

公式的解析

(此公式来源于GCN中，ST-GCN没有做修改)

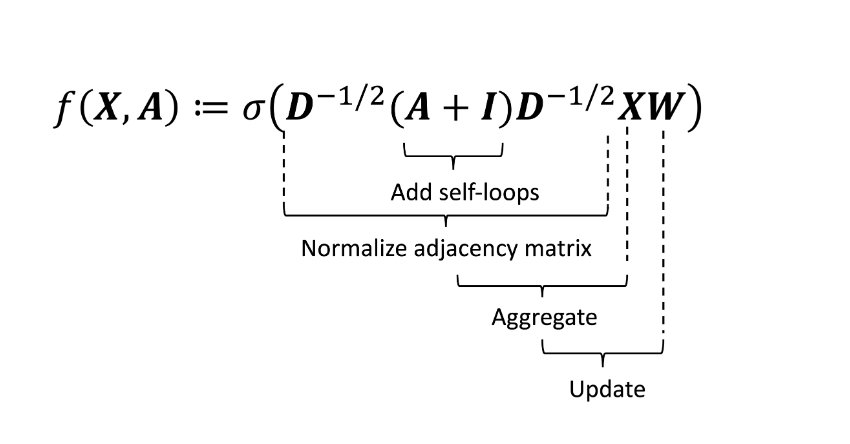
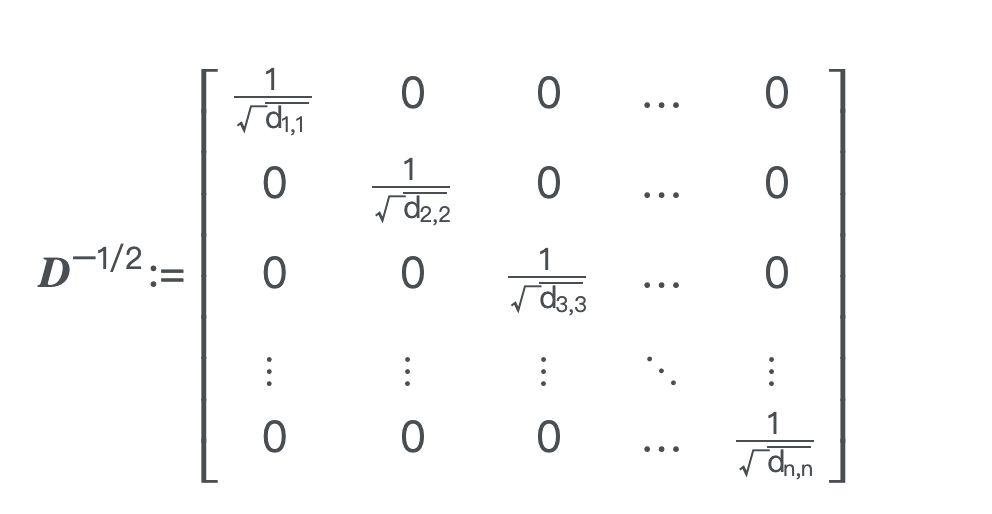
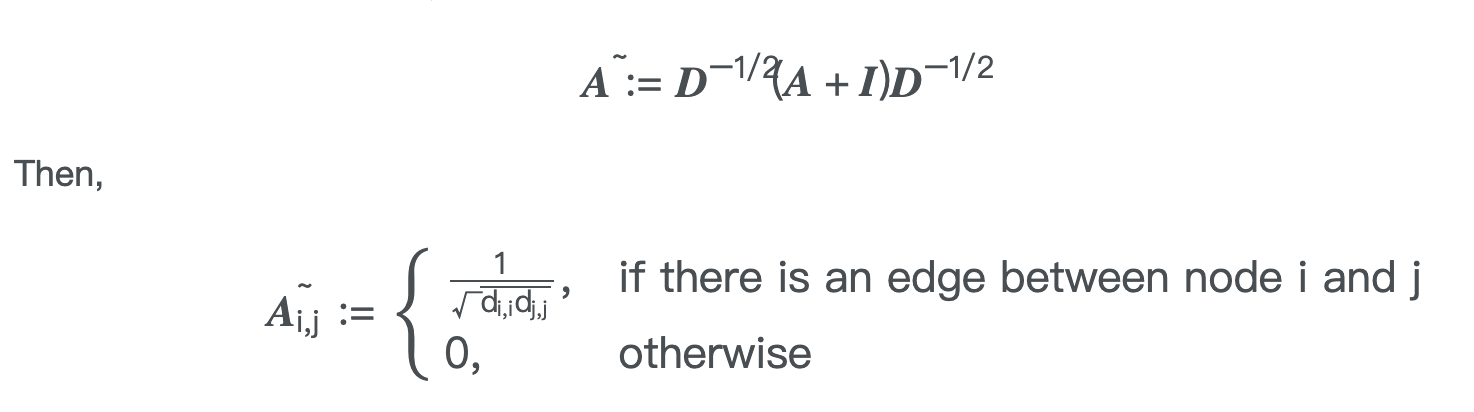
用公式法展开算一遍，就能算出上面的公式。

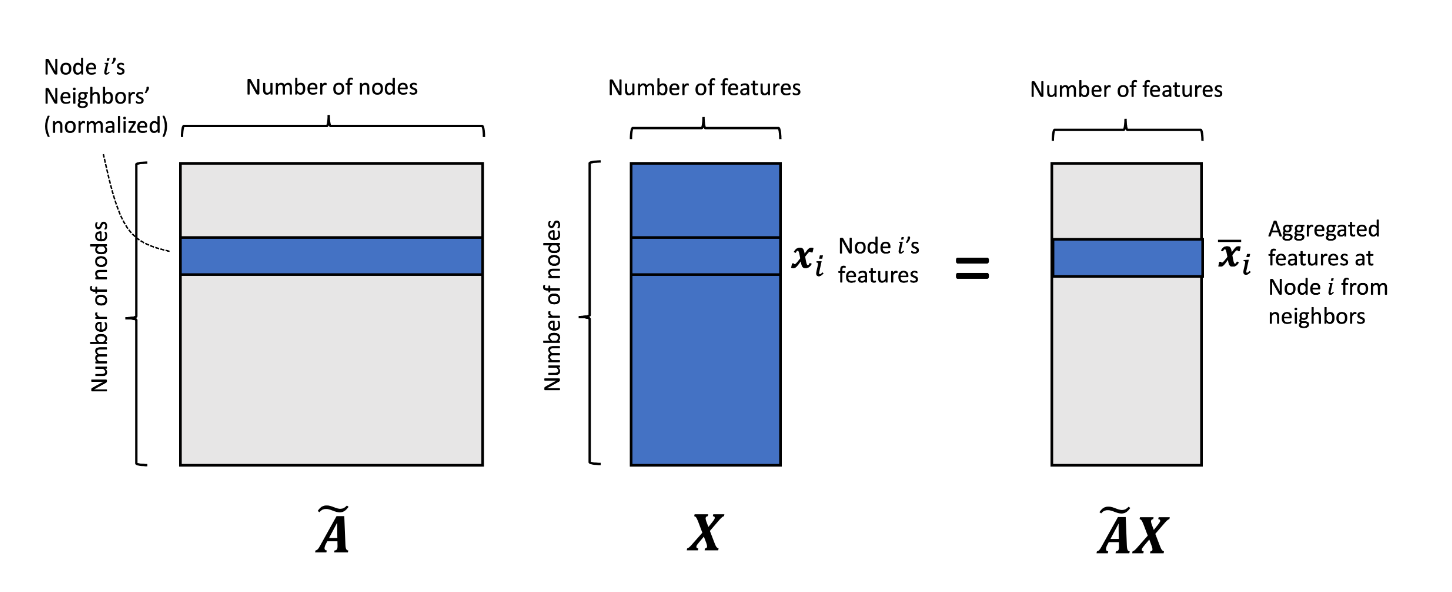
$\begin{aligned}
\bar{\boldsymbol{x}}_i &= \sum_{j=1}^n \tilde{a}_{i,j} \boldsymbol{x}_j \\
&= \sum_{j \in \text{Neigh}(i)} \tilde{a}_{i,j} \boldsymbol{x}_j \\
&= \sum_{j \in \text{Neigh}(i)} \frac{1}{\sqrt{d_{i,i} d_{j,j} } } \boldsymbol{x}_j
\end{aligned}$

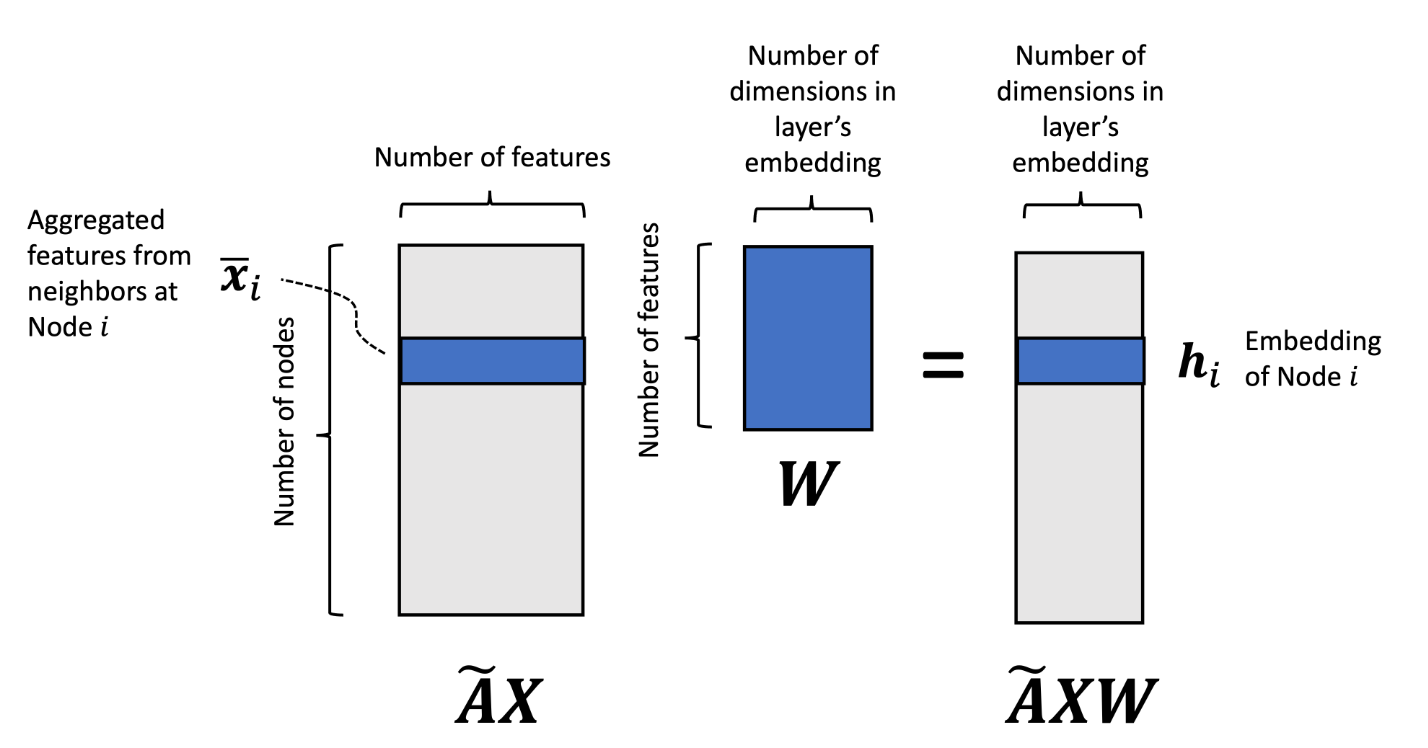
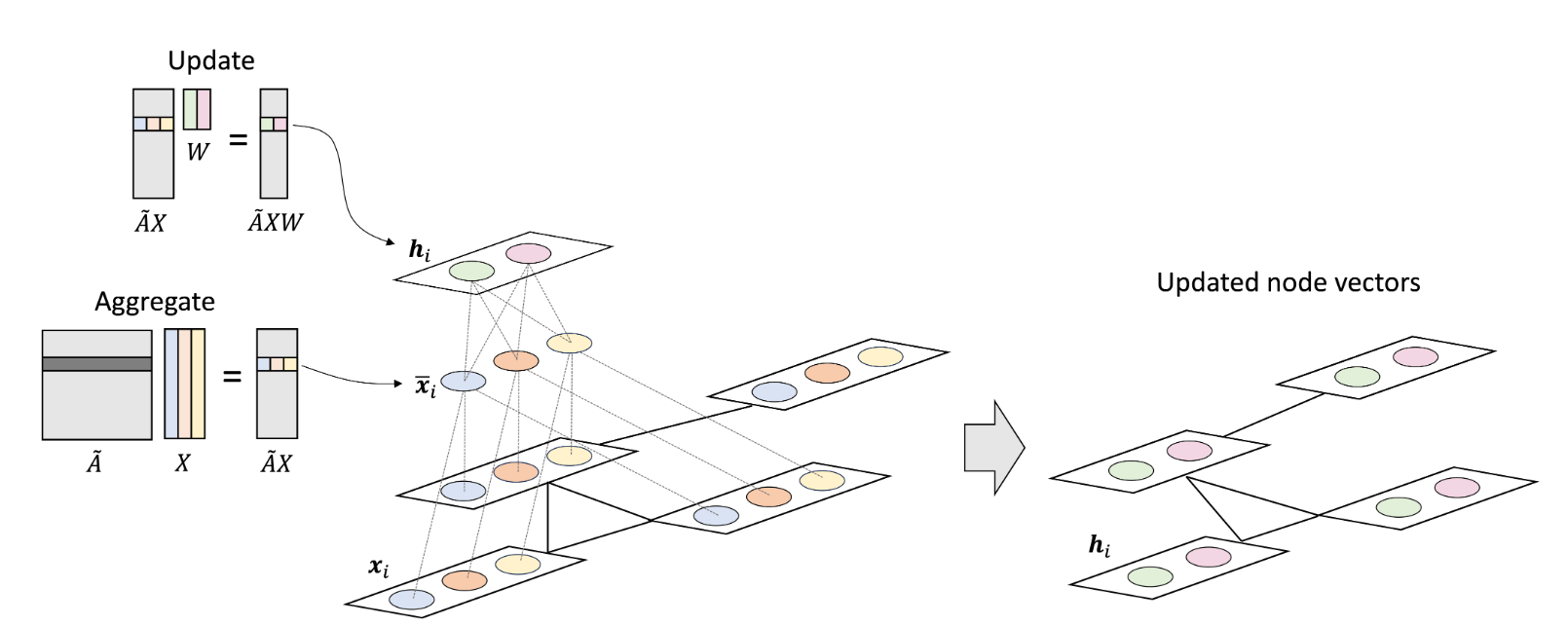
上图中：初始输入$x_i$，经过矩阵$A$，转变为下一层的输入向量。数学表示为：

$\begin{aligned}
\boldsymbol{H}_1 &:= f_{\boldsymbol{W}_1}(\boldsymbol{X}, \boldsymbol{A}) \\ \boldsymbol{H}_2 &:= f_{\boldsymbol{W}_2}(\boldsymbol{H}_1, \boldsymbol{A}) \\ \boldsymbol{H}_3 &:= f_{\boldsymbol{W}_3}(\boldsymbol{H}_2, \boldsymbol{A})
\end{aligned}$

公式计算过程

自环矩阵：$\tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}$
对称归一化：$\tilde{\mathbf{A}}_{\mathrm{norm}}=\Lambda^{-\frac12}\tilde{\mathbf{A}}\Lambda^{-\frac12}$

为什么不采均值归一化，高度节点在聚合过程中，与低度节点具有不同的作用，削弱高度节点的影响，防止多重传播信息爆炸。

保持了数值的稳定性，防止特征信息在传播中过度缩放。
过程：
1. 先右乘$\Lambda^{-\frac12}$：对每个达到节点的邻接节点进行缩放,高度节点，影响被缩小了。
2. 再左乘$\Lambda^{-\frac12}$：对出发节点的邻接节点进行缩放，保持传播平衡，避免单向影响。即添加了信息回传的平衡。
输入特征与邻接矩阵传播: $\tilde{\mathbf{A}}_{\mathrm{norm}}\mathbf{f}_{\mathrm{in}}$每个节点将从它的邻居节点中接收特征并进行聚合。
过程：

$\begin{aligned}
\mathbf{f}_{\mathrm{in}}=\begin{bmatrix}\mathbf{f}_1 \\
\mathbf{f}_2 \\
\vdots \\
\mathbf{f}_N\end{bmatrix}\in\mathbb{R}^{N\times F_{\mathrm{in} } }
\end{aligned}$

特征传播公式：$\mathbf{f}_{\mathrm{prop}}=\mathbf{Af}_{\mathrm{in}}$
对于每个节点$i$，它的新特征$\mathbf{f}_{i,\mathrm{prop}}$，可以表示为：$\mathbf{f}_{i,\mathrm{prop}}=\sum_{j\in\mathcal{N}(i)}A_{ij}\mathbf{f}_j$
其中，$\mathcal{N}(i)$: 表示$i$的所有邻接节点
节点$i$的新特征向量是其所有邻居节点特征向量的加权和

假设$N$个节点，$d_{in}$维的输入特征: $\tilde{\mathbf{A}}_{\mathrm{norm}}f_{\mathrm{in}}$
表示将邻居节点的信息通过归一化邻接矩阵传播给每个节点。每个节点的新特征是根据其相邻节点的特征进行加权求和

使用自连接矩阵，是为了用邻接矩阵算度

其中$\Lambda^{ii}=\sum_j(A^{ij}+I^{ij})$，度矩阵。$\mathbf{W}$多个通道叠加的权重。
实际中在时空的情况下，输入维度为$(C,V,T)$的特征张量。

在有多个子集的分区中，将邻接矩阵分解为几个矩阵：例如距离划分策略中，$\mathbf{A}_0=\mathbf{I}$$ ，\mathbf{A}_1=\mathbf{A}$ 表达式带入得到：
$\mathbf{f}_{out}=\sum_j\boldsymbol{\Lambda}_j^{-\frac12}\mathbf{A}_j\boldsymbol{\Lambda}_j^{-\frac12}\mathbf{f}_{in}\mathbf{W}_j$
将$\Lambda_j^{ii}=\sum_k(A_j^{ik})+\alpha $，$\alpha = 0.001$,避免度矩阵出现空行。

科学系边缘重要性加权的实现：使用一个可学习掩码权重矩阵$\text{M}$，与矩阵进行一个对应位置相乘的算法。用$(\mathbf{A}+\mathbf{I})\otimes\mathbf{M}$代替$(\mathbf{A}+\mathbf{I})$，用$\mathbf{A}_j\otimes\mathbf{M}$代替$\mathbf{A}_j$。$\text{M}$被初始化为全1的矩阵。

网络架构与训练

由于 ST-GCN 在不同节点上共享权重，因此在不同节点上保持输入数据的比例一致是很重要的。首先将输入骨架提供给批处理规范化层来规范化数据。

ST-GCN 模型由9层时空图卷积算子(ST-GCN 单元)组成。前三层有64个输出通道，接着三层有128个输出通道，最后三层有256个输出通道。这些层有9个时间内核大小。Resnet 机制应用于每个 ST-GCN 单元。

在每个 ST-GCN 单元后，我们以0.5概率随机剔除特征，以避免过拟合。第4和第7时序卷积层的步长设为2作为池化层。然后对得到的张量进行全局池化，得到每个序列的256维特征向量。最后，我们将它们输入 SoftMax 分类器。使用随机梯度下降学习模型，学习率为0.01。我们在每10个 epoch 之后将学习率衰减0.1。

为了避免过拟合，我们在动力学数据集上训练时执行两种增强来替换掉层(Kay et al 2017)。

首先，为了模拟相机运动，我们对所有帧的骨架序列执行随机仿射变换。特别是从第一帧到最后一帧，我们选取了几个固定的角度、平移和比例因子作为候选因子，然后随机采样三个因子的两个组合来生成仿射变换。这种转换被插入到中间帧中，以产生一种效果，就好像我们在回放过程中平滑地移动视点一样。我们把这种增强称为随机移动。

其次，我们在训练中从原始骨架序列中随机抽取片段，并在测试中使用所有帧。网络顶部的全局池使网络能够处理不确定长度的输入序列。

不确定长度的输入序列，长视频？

实验

两个数据集：Kinetics 人类动作数据集(Kinetics) (Kay et al 2017)，NTURGB+D (Shahroudy et al 2016)。

首先对动力学数据集进行详细的消融研究，以检查所提出的模型组件对识别性能的贡献。

为了验证我们在无约束设置中获得的经验是否具有普遍性，我们对 NTURGB+D 上的约束设置进行了实验，并将 ST-GCN 与其他最先进的方法进行了比较。所有实验均在 PyTorch 深度学习框架上进行，并配有8个 TITANX 图形处理器。

数据集与评估标准

Kinetics-skeleton数据集

该数据集包含从YouTube检索的大约300000个视频片段。且划分240000个视频片段为训练集、20000个视频片段为验证集。这些视频涵盖了多达400个人类动作类，从日常活动、体育场景到复杂的互动动作。每个视频片段大约10秒。该数据集仅提供没有骨架数据的原始视频片段。

为了获得骨架数据，作者首先将所有视频的分辨率调整为$340×256$，并将帧速率转换为$30 FPS$。然后，作者使用OpenPose姿态估计工具来估计视频片段中的每个帧上的18个关节的位置。OpenPose给出了像素坐标系中的$2D$坐标$(X，Y)$和18个人体关节的置信度得分。因此，作者使用一个元组($X，Y，C)$来表示每个关节，一个骨架帧被记录为一个18元组的数组。对于多人情况，作者在每个片段中选择平均联合置信度最高的2个人。

论文理解

ST-GCN 这篇论文算是 GCN 在骨骼行为识别里面的开山之作了，他提供了一种新的思路和实现方式，解决了以前方法的局限性并取得了较好的效果。虽然他只是2018年发表的，但是这篇论文给了很详细的代码，2019年发表在 CVPR 上的 AS-GCN 和 2s-AGCN 都是在该代码的基础上改进的。

空间特征的提取

1. 图卷积

特征提取器，输入结点特征和图结构，输出结点最终的特征表达。

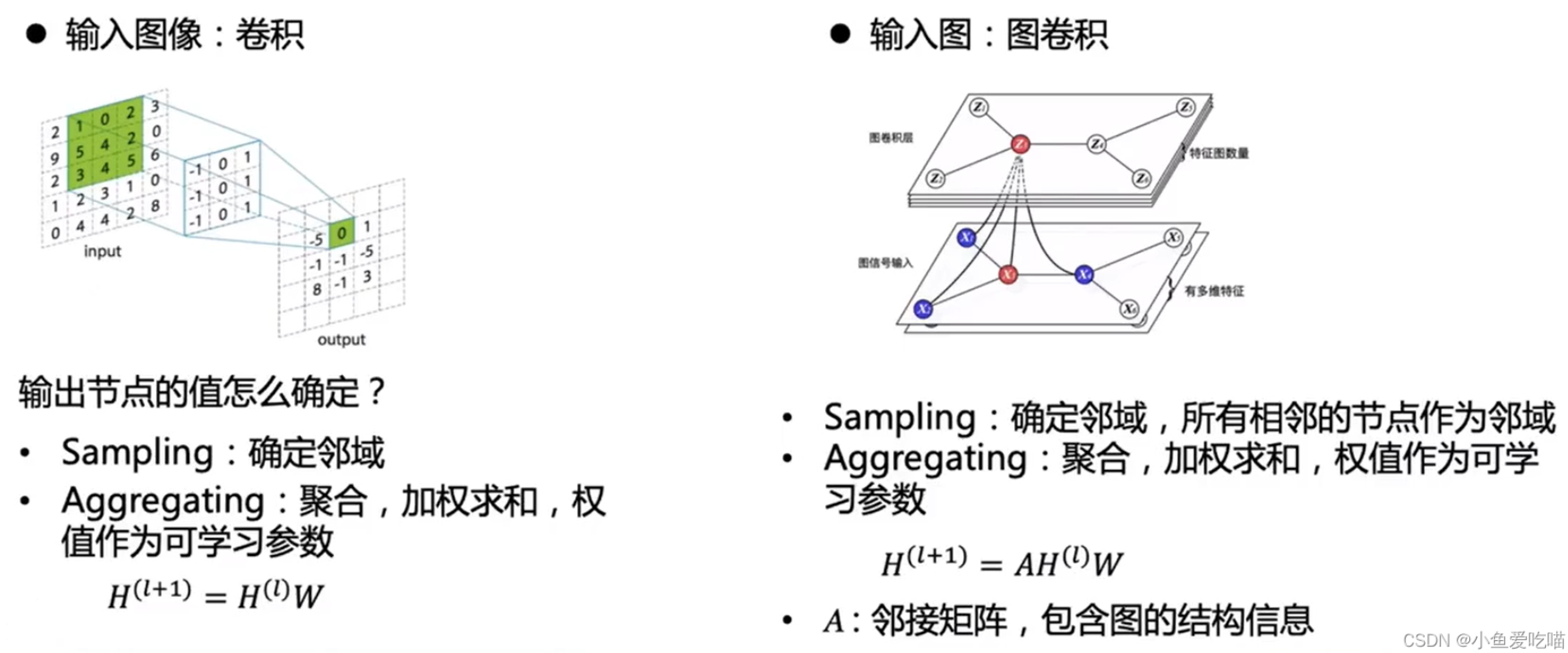
主要的框架就是这样，图卷积相比于图像卷积，只是多左乘了一个邻接矩阵 A，后面就是一些细节。

2. 感受野

一般图像二维卷积最小的卷积核就是 3×3 的卷积核，感受野就是一个中心点和周围八个元素共九个元素的组合。

这里和CNN相似，定义离中心点距离 D=1 ，也就是与中心点直接相连的点为一个卷积核的感受野。如图（a）所示：

3. 卷积核

对应论文中的分区策略。选择的空间结构分区策略

选择合适的感受野和卷积核之后就能够像 CNN 那样一个点一个点的卷积计算了，卷积的过程就是提取特征的过程。

4. 注意力机制

就是增加的可学习权重掩码。

时间特征的提取

整体网络架构

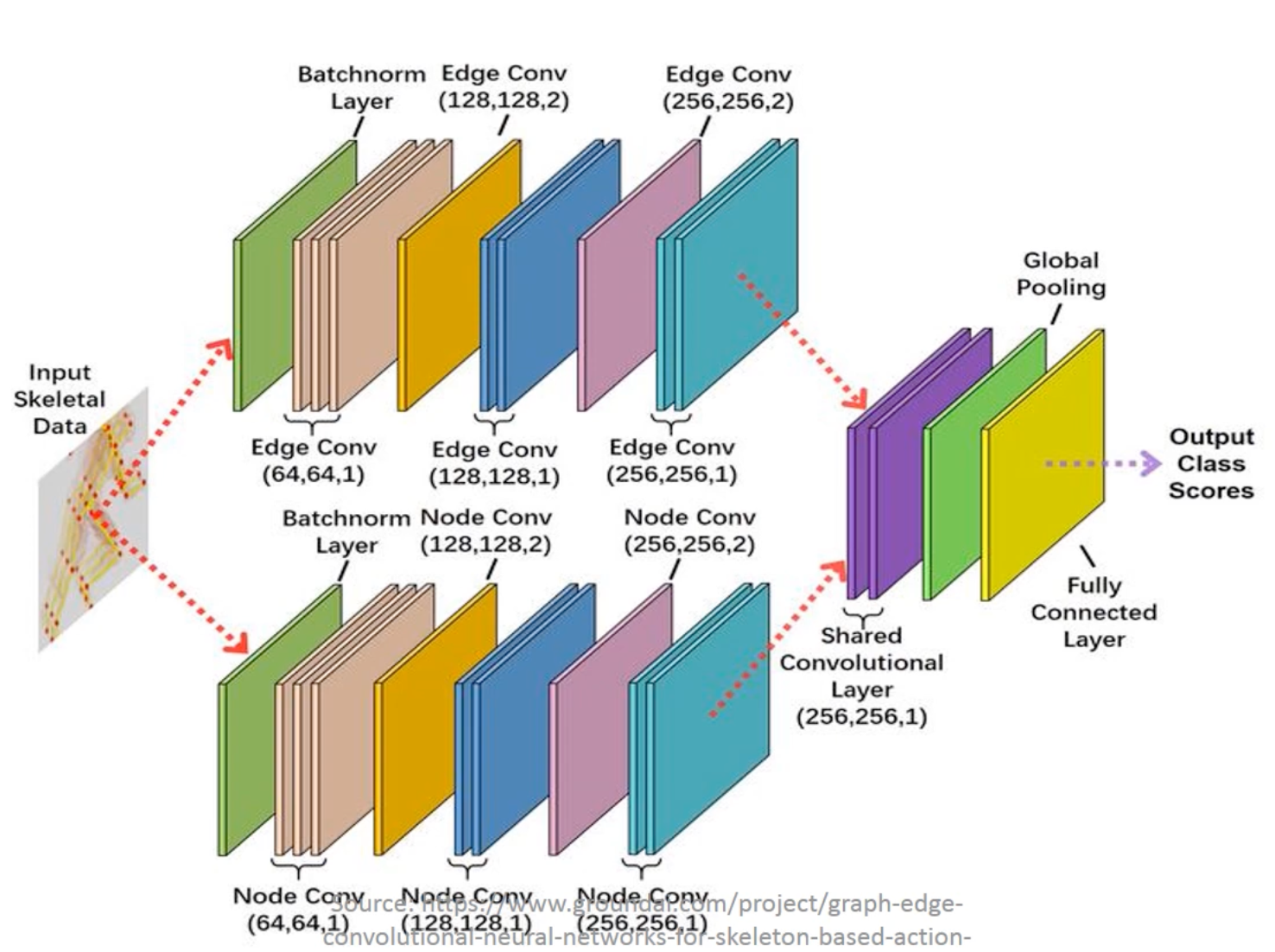
输出格式：

每个通道的数据为(T,V), 代表300帧的18个节点。

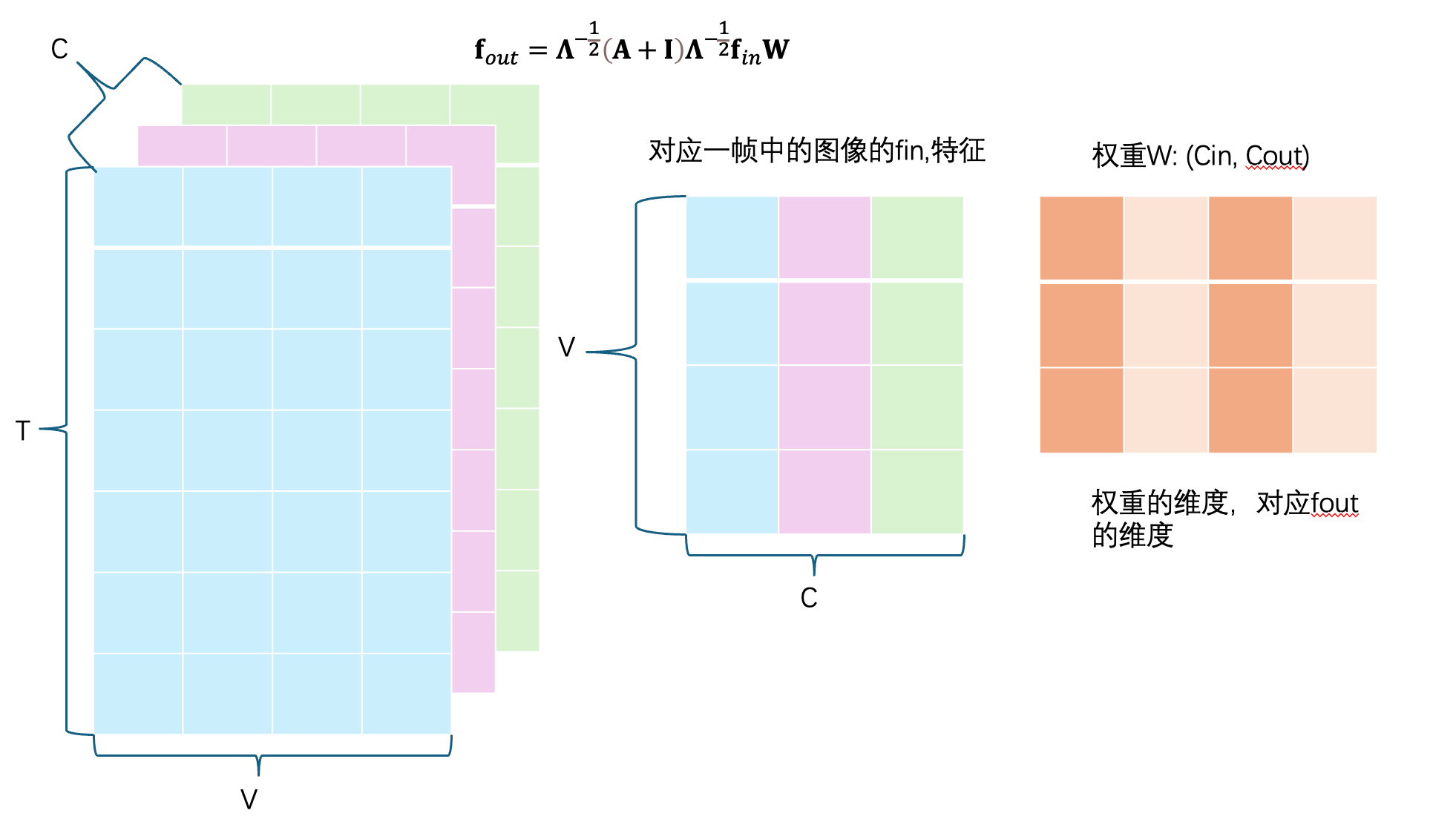
卷积：

空间卷积通过1x1卷积，时间卷积9x1，指的是时间和空间维度，不是通道维度

空间卷积：对所有时间和空间做1x1卷积。`矩阵乘法会转置，图中没有转置`

二维卷积，一个组卷积核，输出一个值。

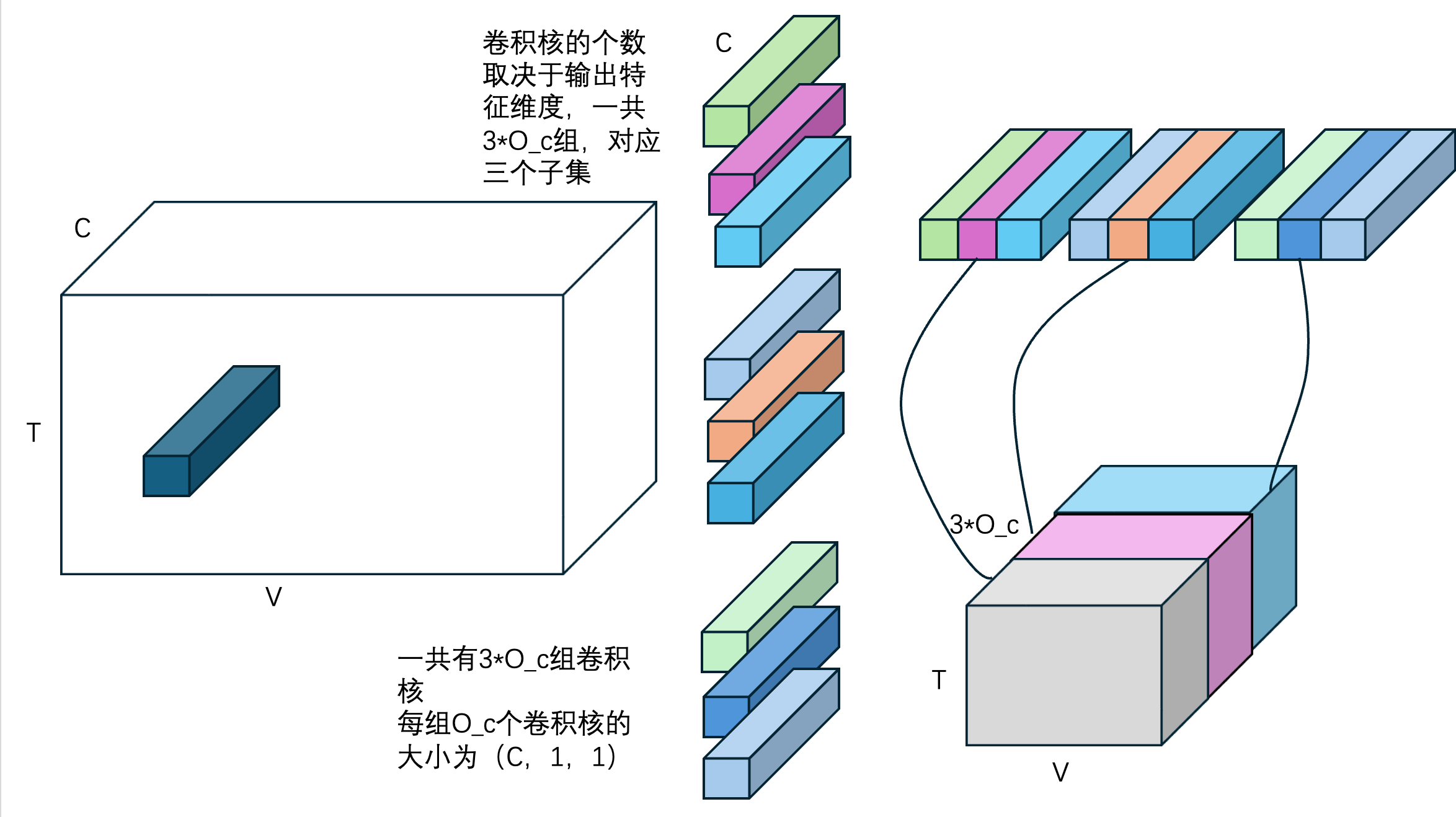
一层GCN中，输出的特征维度为$f_{in}*3$，3来源于子集划分。一共3组卷积核，一组卷积核有$C$个$(1,1,C)$的卷积核。

所有子集特征叠加，不会出问题吗？不应该保留三种子集的特征吗？

不会出问题：三组卷积核处理不同的子集，最后叠加，不属于这个子集的，没有被处理。

时间卷积：

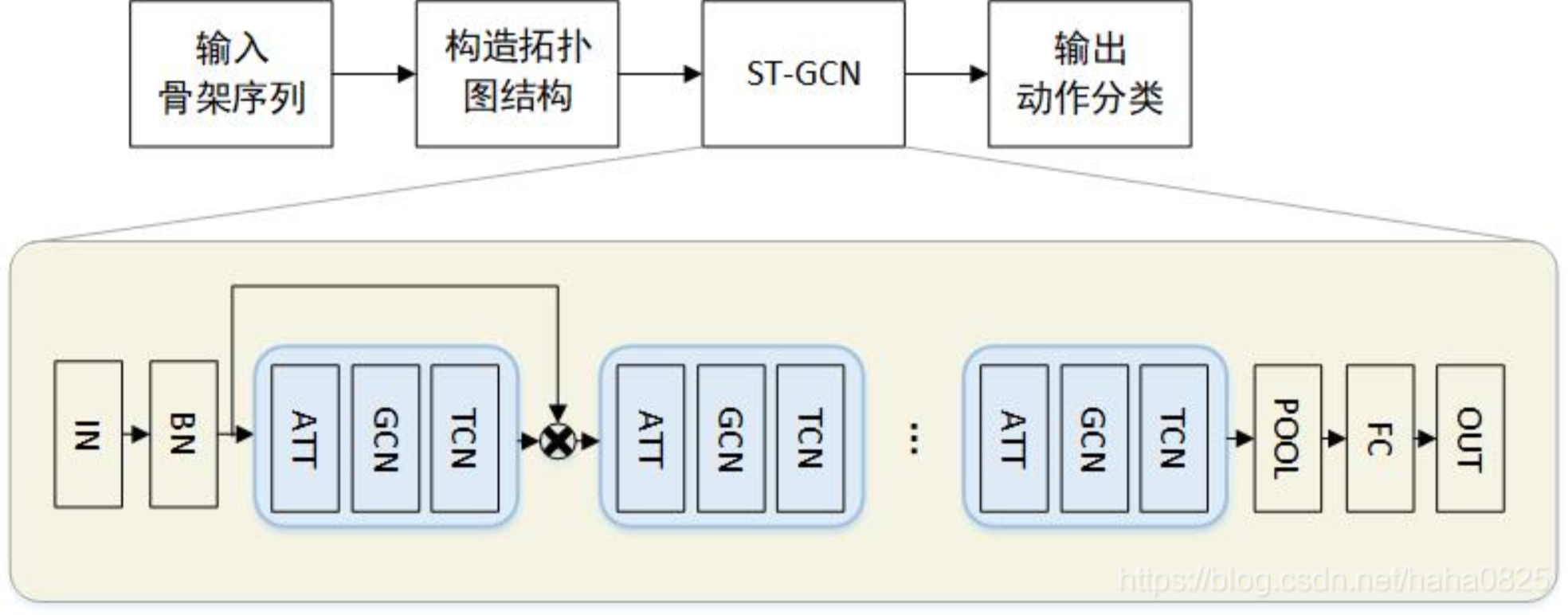
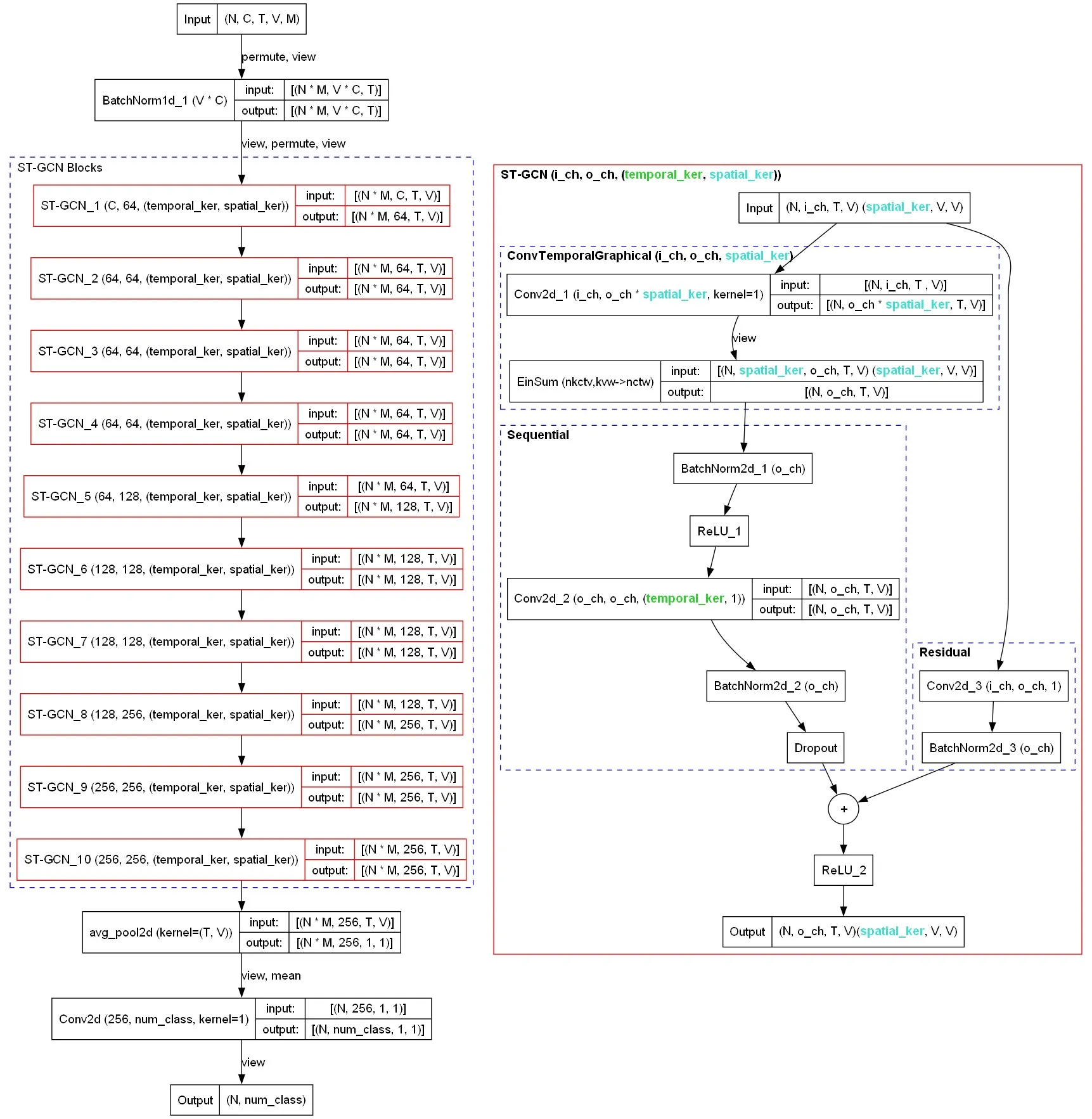
左边是向前传递函数，右边是ST-GCN网络。

N：批量大小。
C：原始节点特征，即（坐标-X/坐标-Y/置信度）三元组。
T：时间步长。
V：图中的节点数。
M：一个帧的数据记录中的骨骼数量。

代码解释：

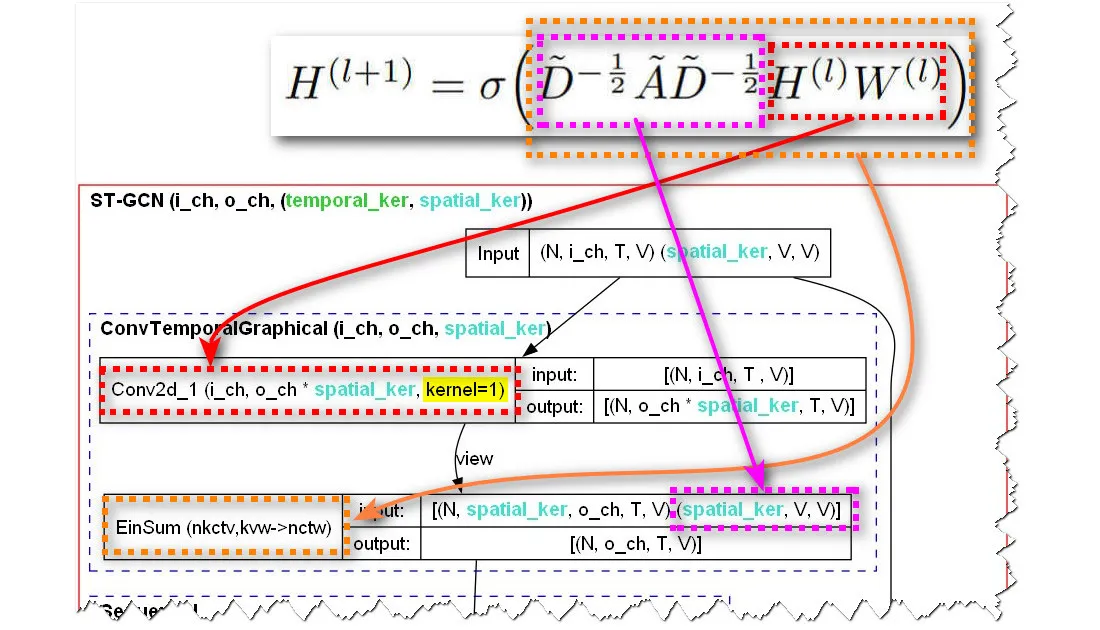
代码的实现是，先进行传递到下层，再进行信息聚合。

爱因斯坦求和

$\text{result}[n,c,t,w]=\sum_{k=1}^K\sum_{v=1}^Vx[n,k,c,t,v]\cdot A[k,v,w]$

对A进行广播，扩充$n$维，公式变为：

$\text{result}[c,t,w]=\sum_{k=1}^K\sum_{v=1}^Vx[k,c,t,v]\cdot A[k,v,w]$

$\text{result}[c,t,w]=\sum_{k=1}^K(\sum_{v=1}^Vx[k,c,t,v]\cdot A[k,v,w])$

对于内部：广播A，变成：$(\sum_{v=1}^Vx[k,c,t,v]\cdot A[k,c,v,w])$

即变为：$\text{result}^1[k,c,t,w]=(\sum_{v=1}^Vx[k,c,t,v]\cdot A[k,c,v,w])$

表示为第k，c维下的第$t$帧的$w$节点的特征，等于第$t$帧所有节点特征乘邻接矩阵$A$的第$w$列向量。(等于聚合了w节点的其他相邻节点特征)

$\text{result}[c,t,w]=\sum_{k=1}^K(\text{result}^1[k,c,t,w])$

表示对新的特征向量进行k重叠加。（把GCN中的输出通道拉长3倍，又消掉了）

与输入对第t帧卷积不同，爱因斯坦求和约定，是对第c通道的第t帧进行的。

也就是说公式计算的是正方体的上截面，而代码计算的是前截面。所以计算方式不同！！

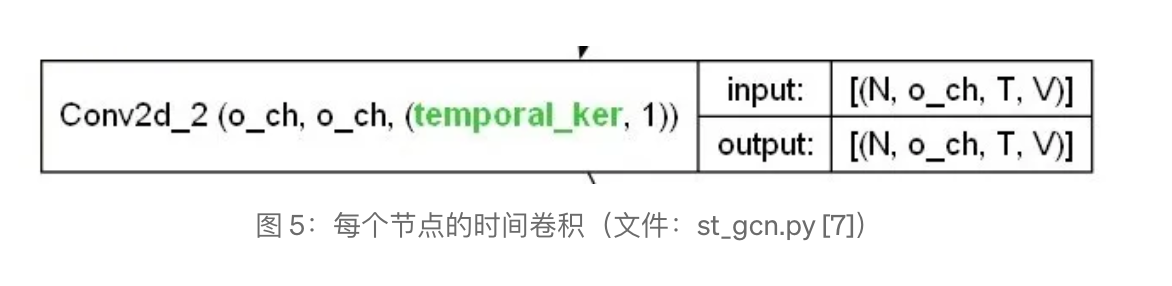
在对节点进行空间卷积之后，它转向对每个节点分别进行时间卷积。我们注意到这里的元组kernel=(temporal_ker, 1)，其中temporal_ker是硬编码的9（9个时间步骤）。

主训练循环在文件“recognition.py” 中定义，其内容很典型。虽然论文中没有讨论，但实现利用了每个 ST-GCN 块中的残差连接（又名跳过连接）来处理梯度退化。由于输入输出通道不同，连接实际上是一个微型神经网络（而不是恒等连接）：

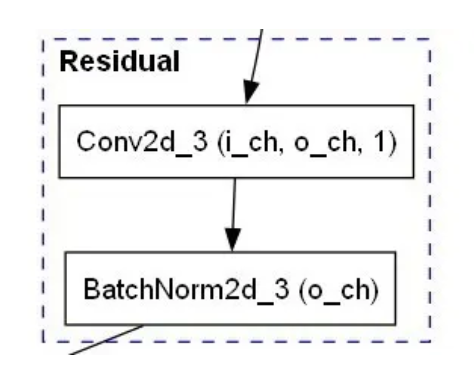
在 ST-GCN 块中，为了防止梯度爆炸并实现更稳定的收敛，在非线性层之前和之后使用 BatchNorm，这是经常建议的。DropOut 层也有助于减少过度拟合。但代码使用 Dropout 的默认设置（意思是：概率0.5），而卷积层的推荐值为0.1或0.2。

ST-GCN的缺点

在上述ST-GCN网络模型的表述中，不难发现，虽然其拥有许多优点，但是ST-GCN的缺点也十分明显：

ST-GCN中的人体骨架图是人为手工定义的，限制后面的网络学习到骨架图中的必要关联与新建连接，例如：在识别如“鼓掌”，“阅读”等与人为手工定义的人体骨架图空间上相距甚远的双手间的关系至关重要的动作时，网络很难学习到其中的关联，也很难对该原本不存在的边进行新建以建立连接，很大程度上降低了动作识别的精度；
除此之外，ST-GCN中的网络结构是分层结构，每一层都代表了不同层次的语义信息，然而作者所采用的是一个全局固定的网络拓扑结构图，导致该网络无法灵活的对各层中的语义进行建模，且由于固定的全局网络拓扑结构，其感受野野不够灵活，也无法提取多尺度的信息；
ST-GCN计算复杂度过高，且由于图卷积各节点之间的信息相互聚合，传统dropout对其无效，导致过拟合，根据此项工作，许多科研人员在此基础上做了大量的相关工作，由于手工定义图的局限性，2s-AGCN与MS-AAGCN引入了多种自适应的拓扑图，而对于分层结构，为方便对各层语义进行建模，SGCN提出了一个通道融合模块 (CAMM)；最后由于高计算复杂度shiftGCN将shift操作引入图卷积代替卷积的特征融合操作，除此之外DC-GCN_ADG提出了DC-GCN（DeCoupling Graph Convolutional Network）图卷积网络，可以在不增加计算量的同时增强图卷积的表达能力，并提出了ADG（attention-guided DropGraph）取代原始dropout，解决了图卷积过拟合的问题。

代码复现

源码结构

config/              包含不同模型训练的配置文件
data/                用于数据加载，处理骨架数据集。
feeder/              数据预处理模块，读取并规范化骨架数据。
models/              训练好的模型参数
net/                包含ST-GCN网络的具体实现和其他模型文件
--utils/            utilities实用工具包含一些通用函数，类或模块
----graph.py        图的定义，节点分集
----tgcn.py          时间图卷积网络
----__init__.py      导入utils包
----st_gcn.py     
----st_gcn_twostream.py
processor/          初始化相关模块
----io.py            模型加载
----processor.py    重载模型加载
----recognition.py  识别模块
resource/            辅助工具，如骨架数据可视化。
tools/              训练、测试和评估的脚本。
torchlight/  
main.py              项目的主入口
requirements.txt    项目所需软件包

环境安装

需要先安装torchlight包, pip安装的版本有问题，需要进入torchlight文件夹，运行stepup.py安装，与pip安装不同，setup.py将文件安装到了/usr/lib/python3.8/site-packages/,

修改安装路径的方式：

python setup.py install --prefix=/usr/local

进入torchlight文件夹，运行pip install .，可以安装成功

远程同步排除文件夹：./data, ./work_dir

net/utils/graph.py

图的定义函数：

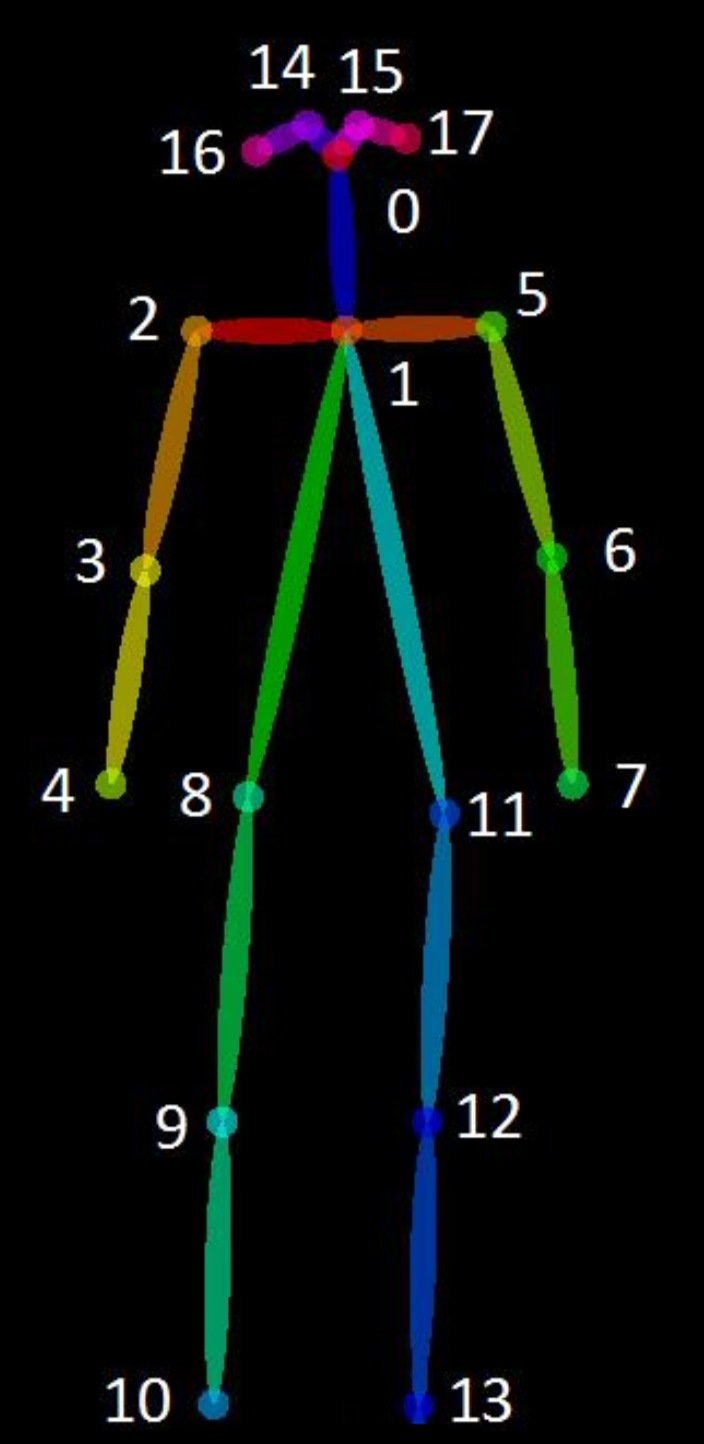
上图表示，openpose关节点邻接顺序。

矩阵的幂运算：np.linalg.matrix_power(A, d):表示邻接矩阵的d跳可达关系。

ST-GCN 时空图卷积神经网路

论文笔记

摘要