计算机视觉 神经网络
更新历史
- 24.05.07:初稿
系列
特征变换
我们从几何学的角度看到了这一点,记得从线性分类器的几何学角度来看,我们认为线性分类器是在画高维超平面,将这个高维的欧几里得空间分割成两块
当我们从视觉角度考虑线性分类器时,我们认为线性分类器只为每个类别学习一个模板,因此它们无法代表同一对象类别的多种模式。
总之,模板是一种用于表示目标对象特征的数据结构,可以采用多种形式。在模板匹配和模板学习任务中,模板被用来在输入数据中搜索和识别目标对象
对于某些线性不可分的数据集,我们可以提出一种特征变换的方式(feature transform),将这些数据映射到特征空间去进行分类,或者说找到一种合适分类的映射方式来完成分类任务,这样就可以克服线性分类器的一些缺点;在这里我们是在特征空间中训练分类器
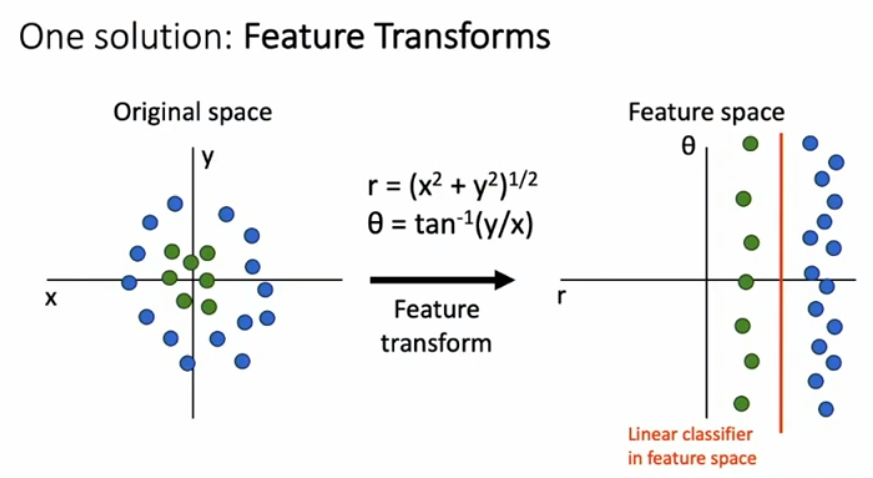
这就是一个将笛卡尔坐标系变换到极坐标系下的例子,这样的话,原本在笛卡尔坐标系下线性不可分的数据集,在极坐标系下线性可分了,也就是说我们可以在特征空间下构建线性分类器
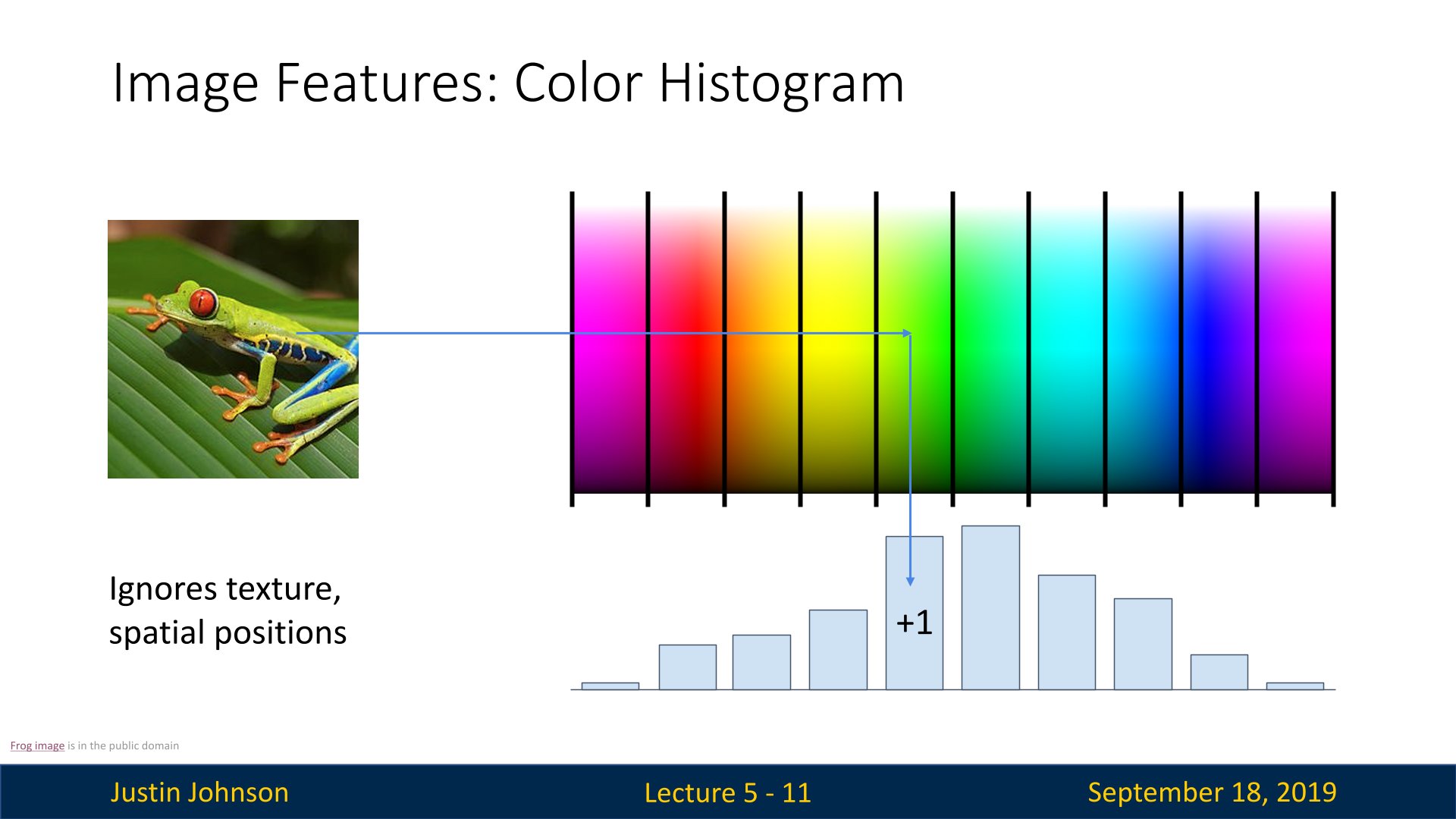
特征变换的思想在计算机视觉中应用广泛,一种就是颜色直方图的概念
我们可以将图像中的颜色空间的RGB光谱进行分解与统计,然后得到颜色直方图,这种方式丢弃了图像中的空间信息,只关心图像中的颜色分布,更具有空间不变性(对不同位置的相同特征可以很好的处理)
图像特征:定向梯度直方图
还有一种进行图像特征提取的方式就是定向梯度直方图
这种方式可以通过一系列处理得到图像的局部梯度信息,具有很好的区分性和鲁棒性,然后,这些特征可以被用于训练分类器
图像特征:词袋模型(数据驱动)
数据驱动,实际上是由我们在训练集中看到的数据驱动的,而数据驱动的特征转换的一个例子就是视觉词袋模型
想法是有一个大型训练数据集,可以提取大量不同比例和大小的随机补丁(也就是从图像上随机切下一小块),然后我们对这些随机补丁进行聚类,就获得了所谓的密码本或者一组视觉词,他们可以表示图像中倾向于出现哪种特征,如果这些补丁在训练集中大量出现,那么我们希望可以学习某种视觉词表示,它可以识别你的训练集中的每一个常见特征
之后的步骤是构建视觉词的代码本,使用学习到的视觉词的代码本来编码你的图像,来表示每个视觉词在单个输入图像中出现了多少次

实际上,2011年的ImageNet挑战赛里面的冠军方案,就是基于这种模型;他们的方案分为两部分:特征提取器和可学习分类器
神经网络概述
在不诉诸大脑的类比的情况下,依然是可以对神经网络算法进行介绍的。在线性分类一节中,在给出图像的情况下,是使用$s=Wx$来计算不同视觉类别的评分,其中$W$是一个矩阵,$x$是一个输入列向量,它包含了图像的全部像素数据。在使用数据库CIFAR-10的案例中,$x$是一个[3072x1]的列向量,$W$是一个[10x3072]的矩阵,所以输出的评分是一个包含10个分类评分的向量。
在之前我们使用线性分类器进行分类,但是接下来我们使用一种两层神经网络来进行学习
神经网络算法不同于线性网络,它的计算公式是$s=W_2max(0,W_1x)$。其中$W_1$的含义是这样的:举个例子来说,它可以是一个[100x3072]的矩阵,其作用是将图像转化为一个100维的过渡向量。函数$max(0,-)$是非线性的,它会作用到每个元素。这个非线性函数有多种选择,后续将会学到。但这个形式是一个最常用的选择,它就是简单地设置阈值,将所有小于0的值变成0。最终,矩阵$W_2$的尺寸是[10x100],因此将得到10个数字,这10个数字可以解释为是分类的评分。注意非线性函数在计算上是至关重要的,如果略去这一步,那么两个矩阵将会合二为一,对于分类的评分计算将重新变成关于输入的线性函数。这个非线性函数就是改变的关键点。参数$W_1,W_2$将通过随机梯度下降来学习到,他们的梯度在反向传播过程中,通过链式法则来求导计算得出。
一个三层的神经网络可以类比地看做$s=W_3max(0,W_2max(0,W_1x))$,其中$W_1,W_2,W_3$是需要进行学习的参数。中间隐层的尺寸是网络的超参数,后续将学习如何设置它们。现在让我们先从神经元或者网络的角度理解上述计算
之前的线性函数为
$
\begin{split}
f=Wx
\end{split}
$
现在使用的两层神经网络为
$
\begin{split}
f=W_2\max(0,W_1x)\\
W_2\in \mathbb{R}^{C\times H}\quad
W_1\in \mathbb{R}^{H\times D}\quad
x\in \mathbb{R}^{D}
\end{split}
$
其中包括两个可学习的权重矩阵$W_1,W_2$,当然在实践过程中,这些向量乘法都会隐式的包含一个可学习的偏差项
当然我们也可以使用这种图形化的形式来表示神经网络,因为其中的每个部分都相互连接,所以也被称为全连接神经网络
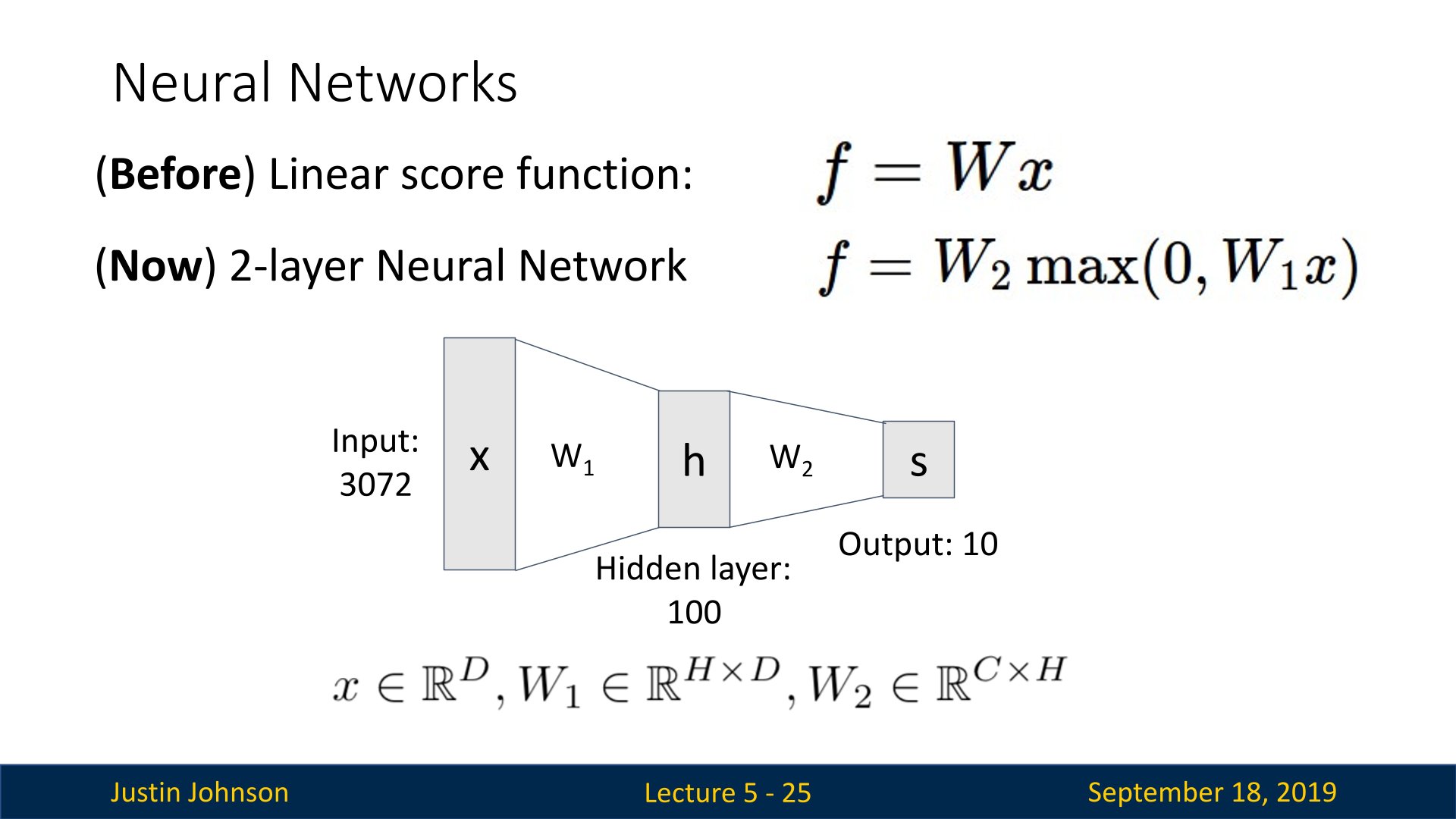
这个激活函数的功能就是可以拓宽神经网络的拟合能力,因为如果有多个线性分类器组合,那么结果还是一个线性分类器,多个分类器等于一个分类器
快速简介
神经网络的几何解释
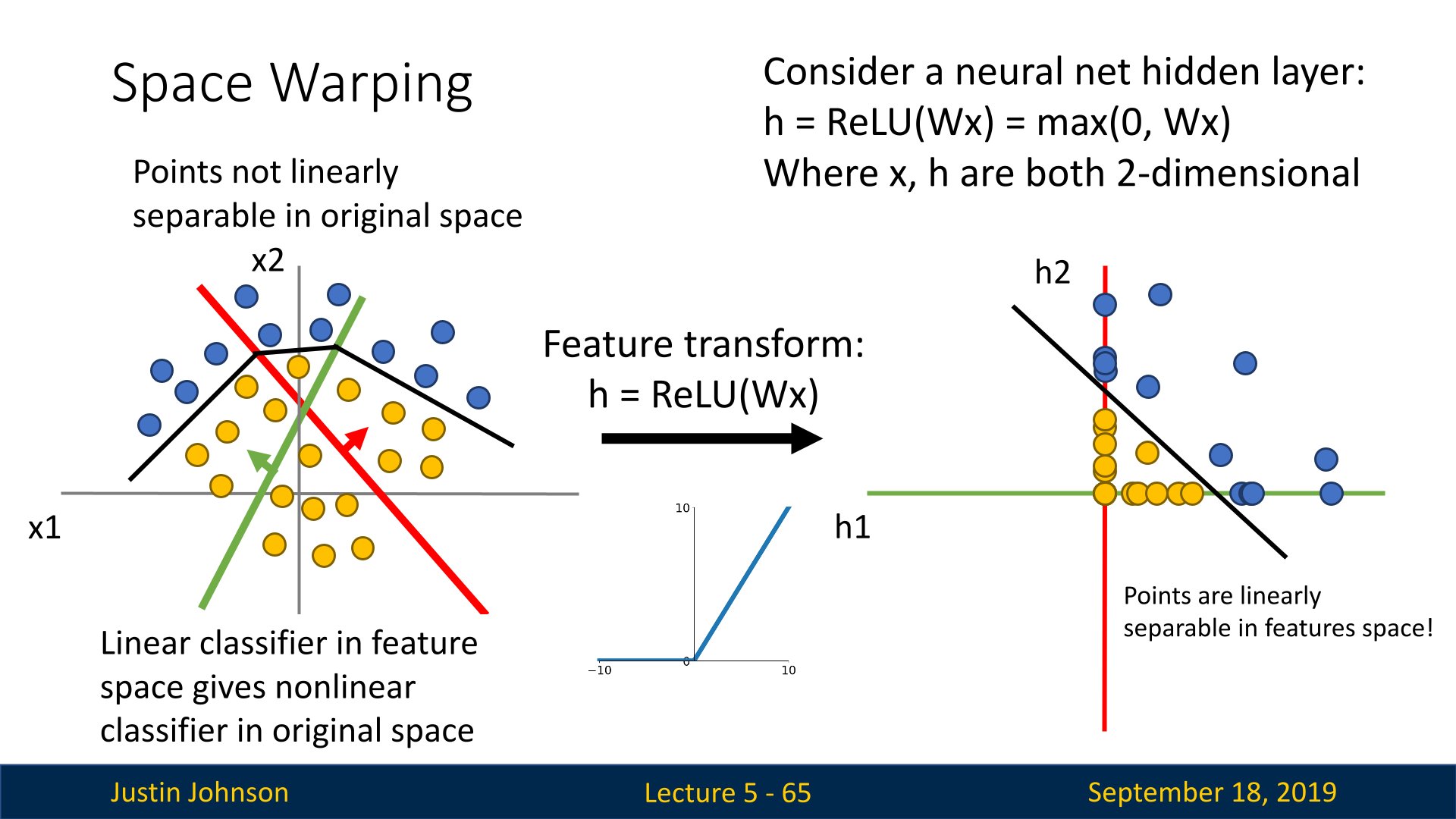
面对一个线性可分的数据集,线性分类器的功能就是找到一个或者多个超平面,可以对不同的数据进行分割,但是存在某些线性不可分的数据集,这个时候,就无法使用超平面进行分割了,或者说找不到一种线性方式进行分割,比如说下面的数据集
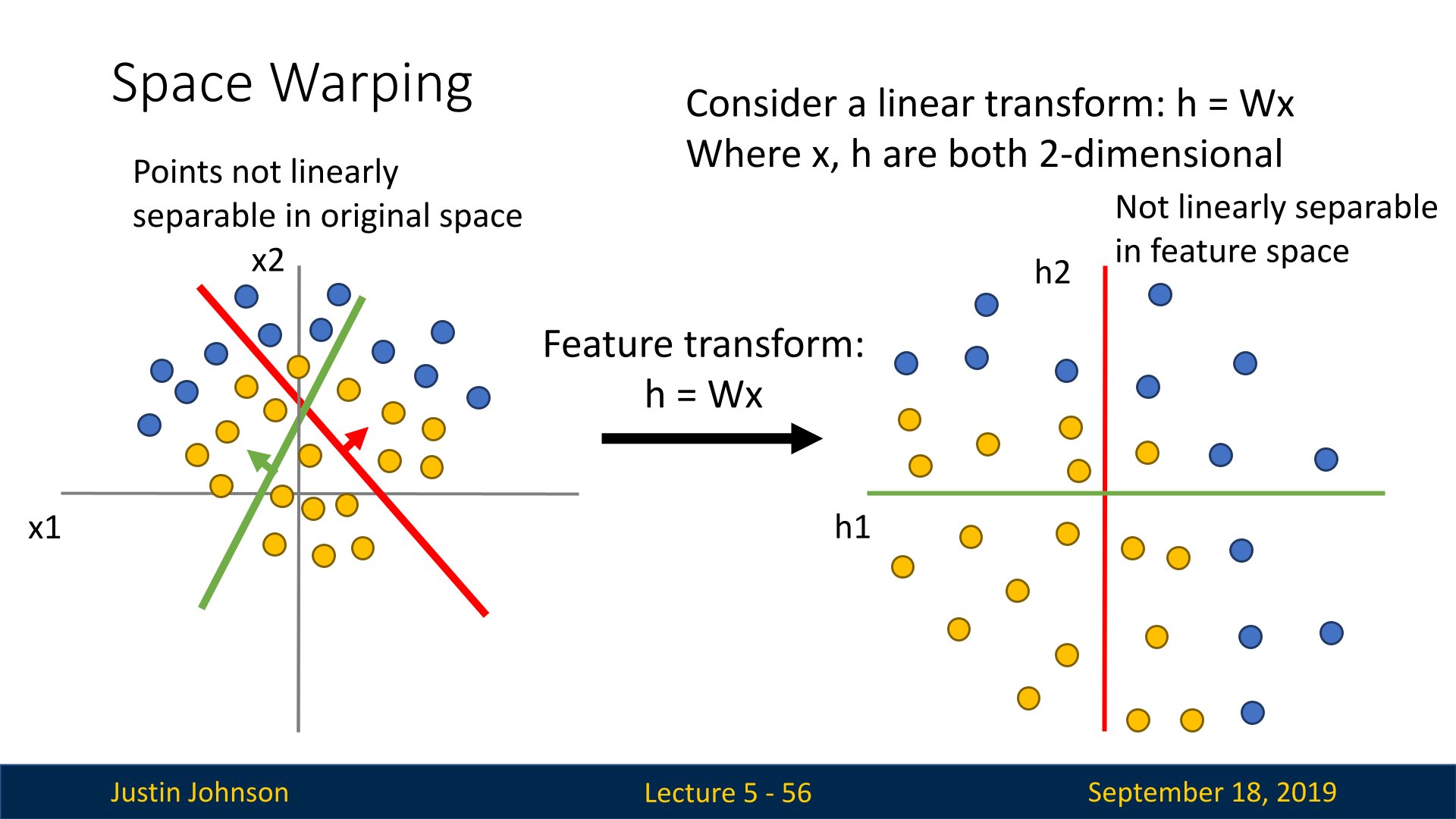
我们发现,找不到一个合适的变换矩阵$W$来分割这个数据集,所以就需要找到一种非线性方式来分割,也就是激活函数的方式,这样就可以完成某些无法线性分割的数据集的分割,比如说下面这种方式,就是使用ReLu函数进行特征变换,然后可以看到,BCD三个区间都并不对应新空间下的三个象限,而是分别落在坐标轴和原点上
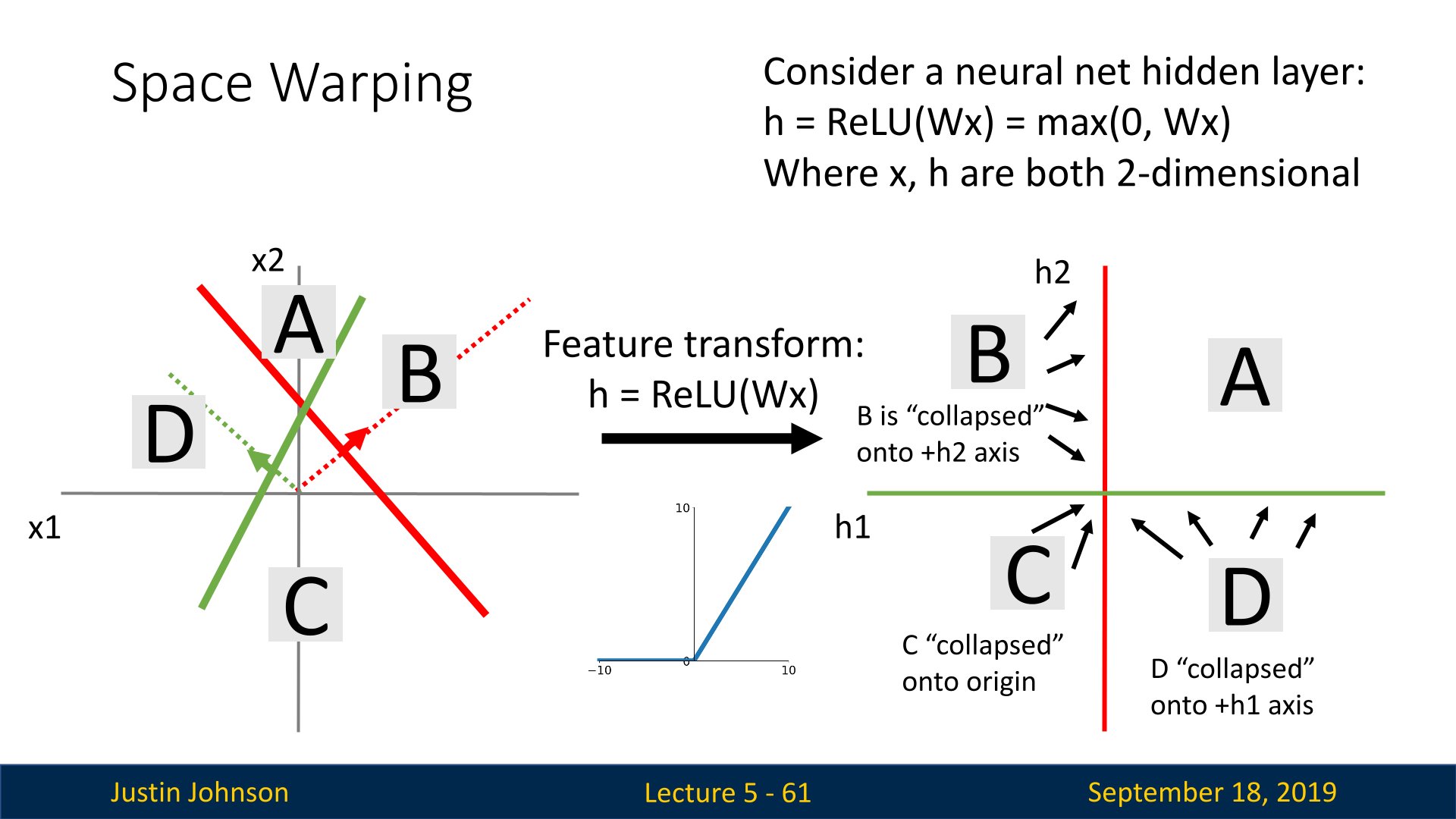
这样,就可以完成某些数据集的分割了,比如说下图
单个神经元建模
神经网络算法领域最初是被对生物神经系统建模这一目标启发,但随后与其分道扬镳,成为一个工程问题,并在机器学习领域取得良好效果。然而,讨论将还是从对生物系统的一个高层次的简略描述开始,因为神经网络毕竟是从这里得到了启发。
生物动机与连接
大脑的基本计算单位是神经元(neuron)。人类的神经系统中大约有860亿个神经元,它们被大约$10^{14}-10^{15}$个突触(synapses)连接起来。下面图表的左边展示了一个生物学的神经元,右边展示了一个常用的数学模型。每个神经元都从它的树突获得输入信号,然后沿着它唯一的轴突(axon)产生输出信号。轴突在末端会逐渐分枝,通过突触和其他神经元的树突相连。
在神经元的计算模型中,沿着轴突传播的信号(比如$x_0$)将基于突触的突触强度(比如$w_0$),与其他神经元的树突进行乘法交互(比如$w_0x_0$)。其观点是,突触的强度(也就是权重$w$),是可学习的且可以控制一个神经元对于另一个神经元的影响强度(还可以控制影响方向:使其兴奋(正权重)或使其抑制(负权重))。在基本模型中,树突将信号传递到细胞体,信号在细胞体中相加。如果最终之和高于某个阈值,那么神经元将会激活,向其轴突输出一个峰值信号。在计算模型中,我们假设峰值信号的准确时间点不重要,是激活信号的频率在交流信息。基于这个速率编码的观点,将神经元的激活率建模为激活函数(activation function)$f$,它表达了轴突上激活信号的频率。由于历史原因,激活函数常常选择使用sigmoid函数$\sigma$,该函数输入实数值(求和后的信号强度),然后将输入值压缩到0-1之间。在本节后面部分会看到这些激活函数的各种细节。
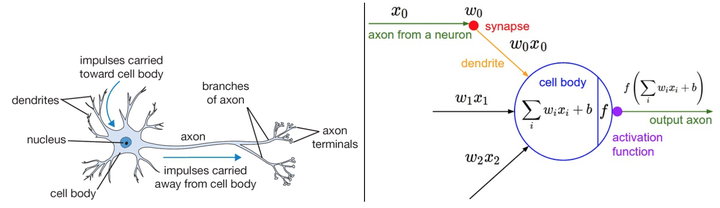
左边是生物神经元,右边是数学模型。
一个神经元前向传播的实例代码如下:
class Neuron(object):
# ...
def forward(inputs):
""" 假设输入和权重是1-D的numpy数组,偏差是一个数字 """
cell_body_sum = np.sum(inputs * self.weights) + self.bias
firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid激活函数
return firing_rate
换句话说,每个神经元都对它的输入和权重进行点积,然后加上偏差,最后使用非线性函数(或称为激活函数)。本例中使用的是sigmoid函数$\sigma(x)=1/(1+e^{-x})$。在本节的末尾部分将介绍不同激活函数的细节。
粗糙模型:要注意这个对于生物神经元的建模是非常粗糙的:在实际中,有很多不同类型的神经元,每种都有不同的属性。生物神经元的树突可以进行复杂的非线性计算。突触并不就是一个简单的权重,它们是复杂的非线性动态系统。很多系统中,输出的峰值信号的精确时间点非常重要,说明速率编码的近似是不够全面的。鉴于所有这些已经介绍和更多未介绍的简化,如果你画出人类大脑和神经网络之间的类比,有神经科学背景的人对你的板书起哄也是非常自然的。
作为线性分类器的单个神经元
神经元模型的前向计算数学公式看起来可能比较眼熟。就像在线性分类器中看到的那样,神经元有能力”喜欢”(激活函数值接近1),或者不喜欢(激活函数值接近0)输入空间中的某些线性区域。因此,只要在神经元的输出端有一个合适的损失函数,就能让单个神经元变成一个线性分类器。
二分类Softmax分类器。举例来说,可以把$\displaystyle\sigma(\sigma_iw_ix_i+b)$看做其中一个分类的概率$P(y_i=1|x_i;w)$,其他分类的概率为$P(y_i=0|x_i;w)=1-P(y_i=1|x_i;w)$,因为它们加起来必须为1。根据这种理解,可以得到交叉熵损失,这个在线性分一节中已经介绍。然后将它最优化为二分类的Softmax分类器(也就是逻辑回归)。因为sigmoid函数输出限定在0-1之间,所以分类器做出预测的基准是神经元的输出是否大于0.5。
二分类SVM分类器。或者可以在神经元的输出外增加一个最大边界折叶损失(max-margin hinge loss)函数,将其训练成一个二分类的支持向量机。
理解正则化。在SVM/Softmax的例子中,正则化损失从生物学角度可以看做逐渐遗忘,因为它的效果是让所有突触权重$w$在参数更新过程中逐渐向着0变化。
> 一个单独的神经元可以用来实现一个二分类分类器,比如二分类的Softmax或者SVM分类器。
常用激活函数
激活函数是一种很有用的方式,可以增强模型的拟合能力,来完成对各种数据的拟合
每个激活函数(或非线性函数)的输入都是一个数字,然后对其进行某种固定的数学操作。下面是在实践中可能遇到的几种激活函数:
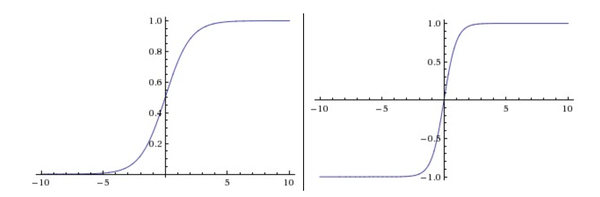
左边是Sigmoid非线性函数,将实数压缩到[0,1]之间。右边是tanh函数,将实数压缩到[-1,1]。
Sigmoid。sigmoid非线性函数的数学公式是$\displaystyle\sigma(x)=1/(1+e^{-x})$,函数图像如上图的左边所示。在前一节中已经提到过,它输入实数值并将其”挤压”到0到1范围内。更具体地说,很大的负数变成0,很大的正数变成1。在历史上,sigmoid函数非常常用,这是因为它对于神经元的激活频率有良好的解释:从完全不激活(0)到在求和后的最大频率处的完全饱和(saturated)的激活(1)。然而现在sigmoid函数已经不太受欢迎,实际很少使用了,这是因为它有两个主要缺点:
- _ Sigmoid函数饱和使梯度消失_。sigmoid神经元有一个不好的特性,就是当神经元的激活在接近0或1处时会饱和:在这些区域,梯度几乎为0。回忆一下,在反向传播的时候,这个(局部)梯度将会与整个损失函数关于该门单元输出的梯度相乘。因此,如果局部梯度非常小,那么相乘的结果也会接近零,这会有效地”杀死”梯度,几乎就有没有信号通过神经元传到权重再到数据了。还有,为了防止饱和,必须对于权重矩阵初始化特别留意。比如,如果初始化权重过大,那么大多数神经元将会饱和,导致网络就几乎不学习了。
- _Sigmoid函数的输出不是零中心的_。这个性质并不是我们想要的,因为在神经网络后面层中的神经元得到的数据将不是零中心的。这一情况将影响梯度下降的运作,因为如果输入神经元的数据总是正数(比如在$f=w^Tx+b$中每个元素都$x>0$),那么关于$w$的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数(具体依整个表达式$f$而定)。这将会导致梯度下降权重更新时出现z字型的下降。然而,可以看到整个批量的数据的梯度被加起来后,对于权重的最终更新将会有不同的正负,这样就从一定程度上减轻了这个问题。因此,该问题相对于上面的神经元饱和问题来说只是个小麻烦,没有那么严重。
Tanh。tanh非线性函数图像如上图右边所示。它将实数值压缩到[-1,1]之间。和sigmoid神经元一样,它也存在饱和问题,但是和sigmoid神经元不同的是,它的输出是零中心的。因此,在实际操作中,_tanh非线性函数比sigmoid非线性函数更受欢迎_。注意tanh神经元是一个简单放大的sigmoid神经元,具体说来就是:$tanh(x)=2\sigma(2x)-1$。
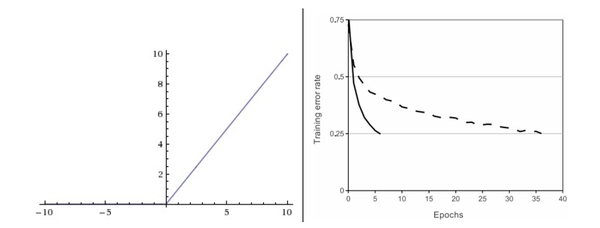
左边是ReLU(校正线性单元:Rectified Linear Unit)激活函数,当$x=0$时函数值为0。当$x>0$函数的斜率为1。
ReLU。在近些年ReLU变得非常流行。它的函数公式是$f(x)=max(0,x)$。换句话说,这个激活函数就是一个关于0的阈值(如上图左侧)。使用ReLU有以下一些优缺点:
- 优点:相较于sigmoid和tanh函数,ReLU对于随机梯度下降的收敛有巨大的加速作用。据称这是由它的线性,非饱和的公式导致的。
- 优点:sigmoid和tanh神经元含有指数运算等耗费计算资源的操作,而ReLU可以简单地通过对一个矩阵进行阈值计算得到。
- 缺点:在训练的时候,ReLU单元比较脆弱并且可能”死掉”。举例来说,当一个很大的梯度流过ReLU的神经元的时候,可能会导致梯度更新到一种特别的状态,在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生,那么从此所以流过这个神经元的梯度将都变成0。也就是说,这个ReLU单元在训练中将不可逆转的死亡,因为这导致了数据多样化的丢失。例如,如果学习率设置得太高,可能会发现网络中40%的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。通过合理设置学习率,这种情况的发生概率会降低。
Leaky ReLU。Leaky ReLU是为解决”ReLU死亡”问题的尝试。ReLU中当x<0时,函数值为0。而Leaky ReLU则是给出一个很小的负数梯度值,比如0.01。所以其函数公式为$f(x)=max(0,x)+\alpha\cdot min(0,x)$其中$\alpha$是一个小的常量。有些研究者的论文指出这个激活函数表现很不错,但是其效果并不是很稳定。Kaiming He等人在2015年发布的论文中介绍了一种新方法PReLU,把负区间上的斜率当做每个神经元中的一个参数。然而该激活函数在在不同任务中均有益处的一致性并没有特别清晰。
Maxout。一些其他类型的单元被提了出来,它们对于权重和数据的内积结果不再使用$f(w^Tx+b)$函数形式。一个相关的流行选择是Maxout神经元。Maxout是对ReLU和leaky ReLU的一般化归纳,它的函数是:$max(w^T_1x+b_1,w^T_2x+b_2)$。ReLU和Leaky ReLU都是这个公式的特殊情况(比如ReLU就是当$w_1,b_1=0$的时候)。这样Maxout神经元就拥有ReLU单元的所有优点(线性操作和不饱和),而没有它的缺点(死亡的ReLU单元)。然而和ReLU对比,它每个神经元的参数数量增加了一倍,这就导致整体参数的数量激增。
以上就是一些常用的神经元及其激活函数。最后需要注意一点:在同一个网络中混合使用不同类型的神经元是非常少见的,虽然没有什么根本性问题来禁止这样做。
一句话:”那么该用那种呢?”用ReLU非线性函数。注意设置好学习率,或许可以监控你的网络中死亡的神经元占的比例。如果单元死亡问题困扰你,就试试Leaky ReLU或者Maxout,不要再用sigmoid了。也可以试试tanh,但是其效果应该不如ReLU或者Maxout。