计算机视觉概论 光反射成像,亮度,阴影
更新历史
- 24.05.03:初稿
系列
图像的成像
表面纹理
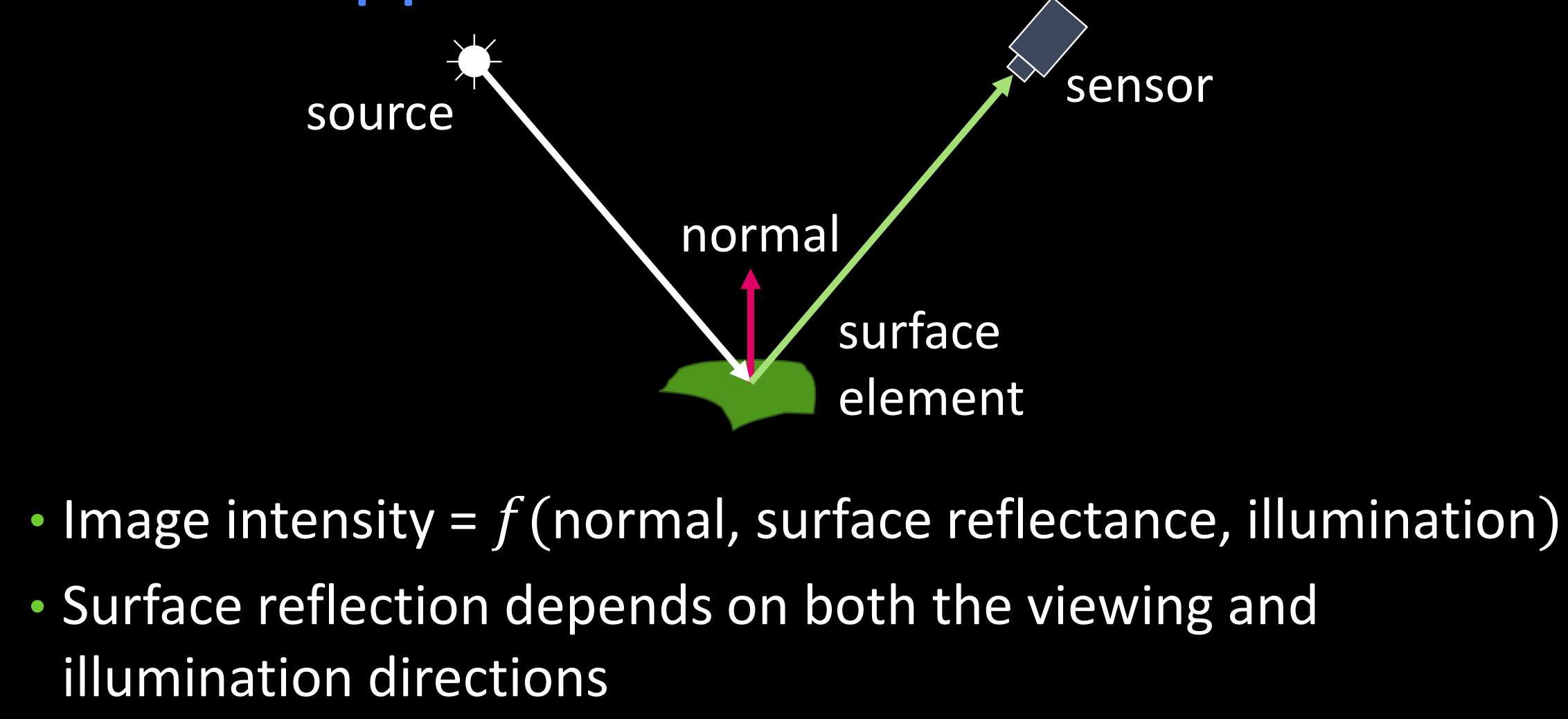
图像由:一小块表面法线,表面折射率,照明组成。
辐射率
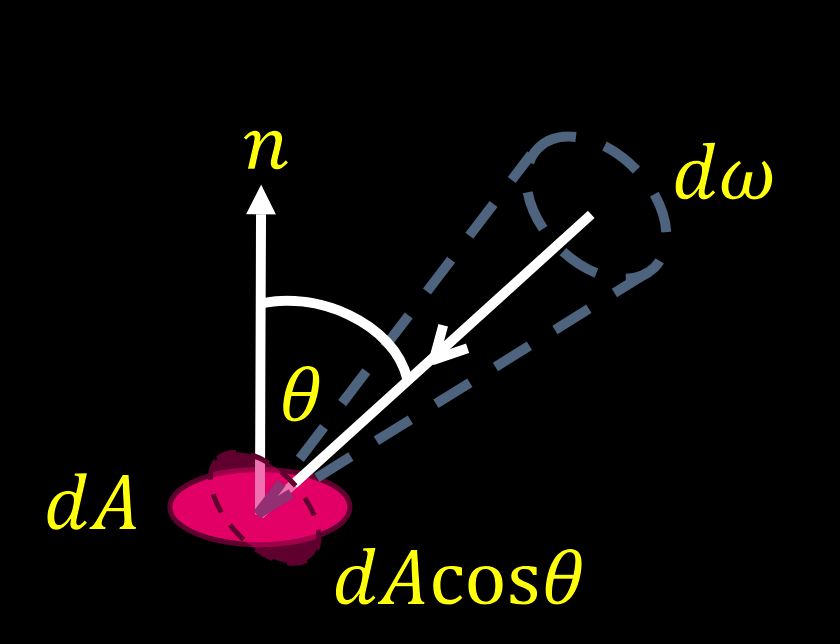
辐射率:单位面积上吸收的能量
单位:瓦每平方米 $Wm^{-2}Sr^{-1}$
到达表面的能量:E
单位:$Wm^{-2}$

双向反射分布函数 BRDF
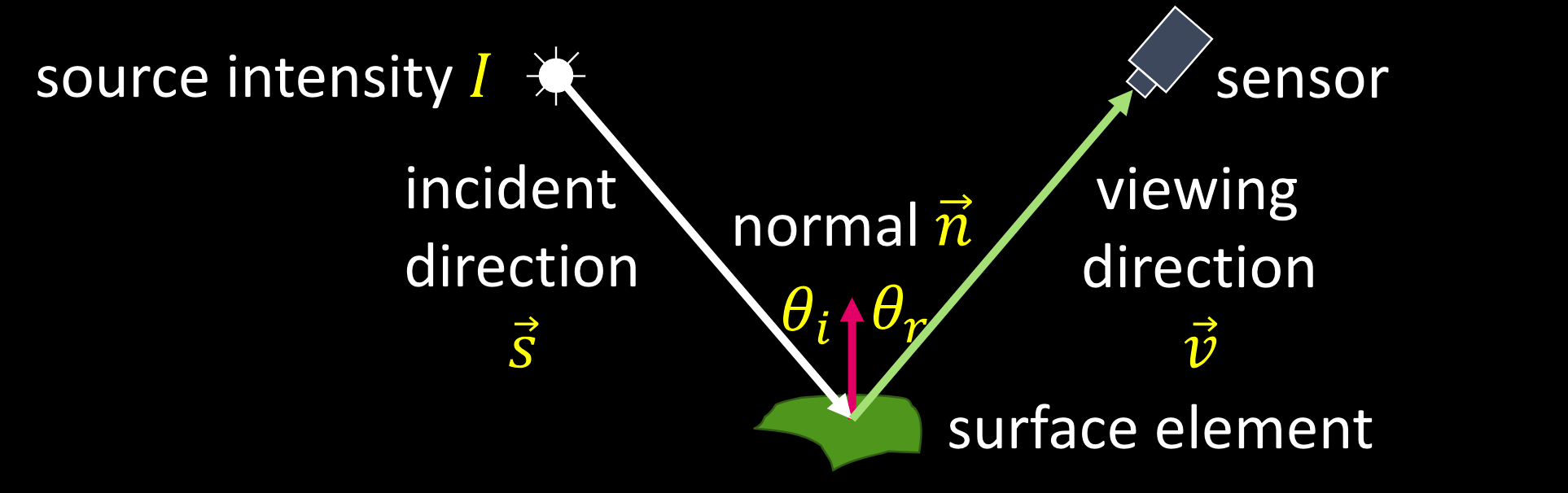
入射,反射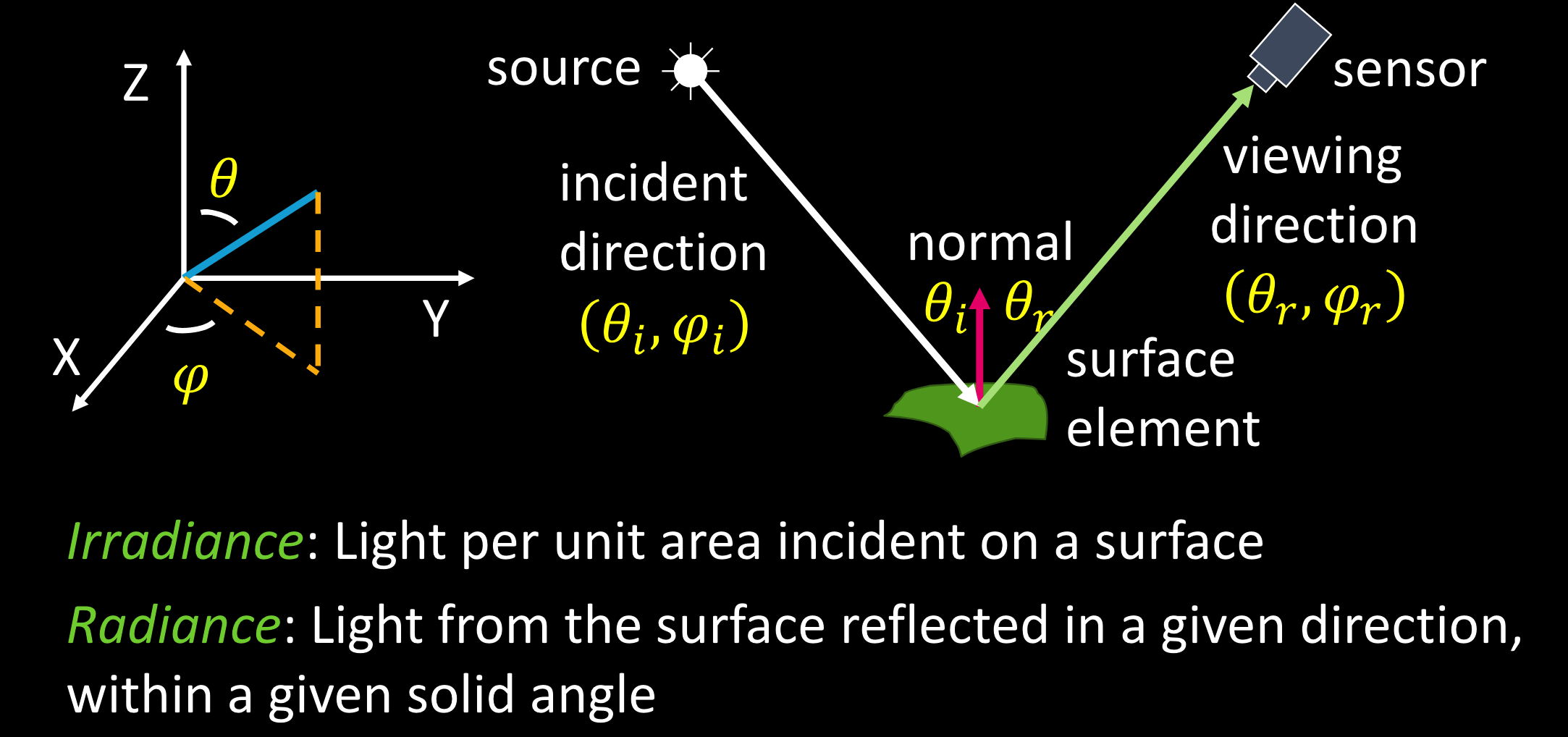

BRDF公式:$f(\theta_i,\varphi_i;\theta_r,\varphi_r)=\frac{L^{surface}(\theta_r,\varphi_r)}{E^{surface}(\theta_i,\varphi_i)}$
反射与入射的比例
重要属性:
交换光源和照相机,比例不变:
$f(\theta_i,\varphi_i;\theta_r,\varphi_r)=f(\theta_r,\varphi_r;\theta_i,\varphi_i)$
旋转对称性:
$f(\theta_i,\varphi_i;\theta_r,\varphi_r)=f(\theta_i,\theta_r,\varphi_i-\varphi_r)$
表明公式与绝对角度无关,只有他们之间的相对角度有关。
反射模型
漫反射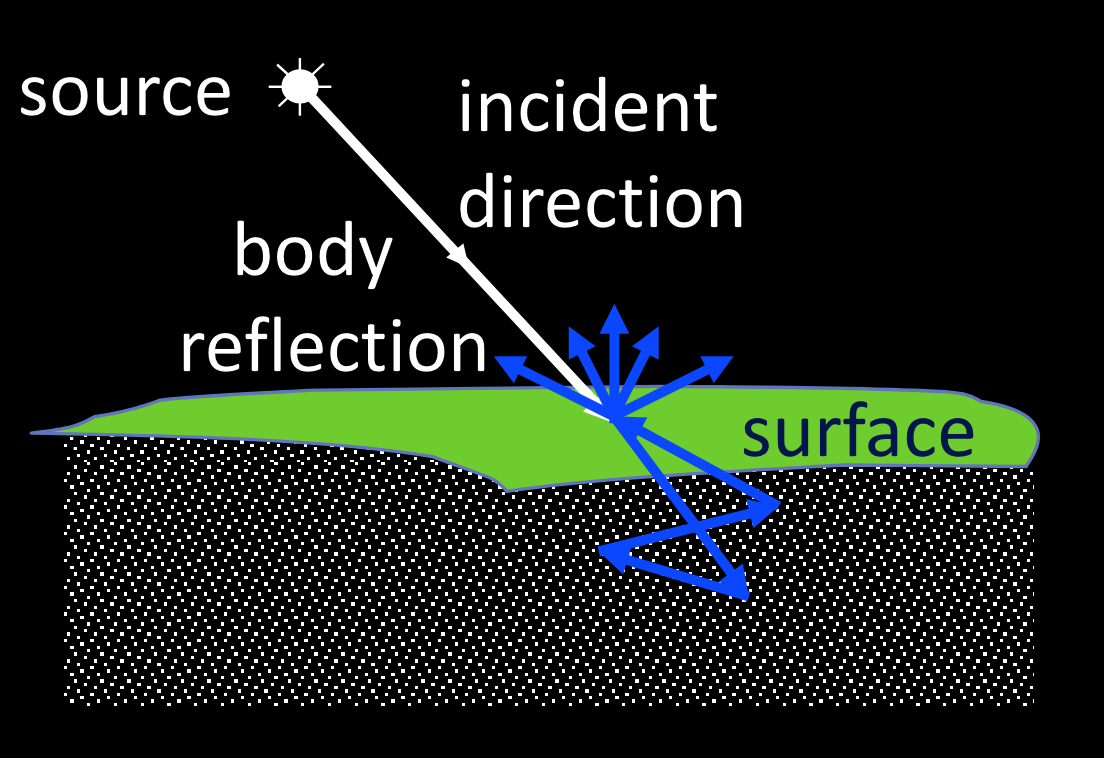
镜面反射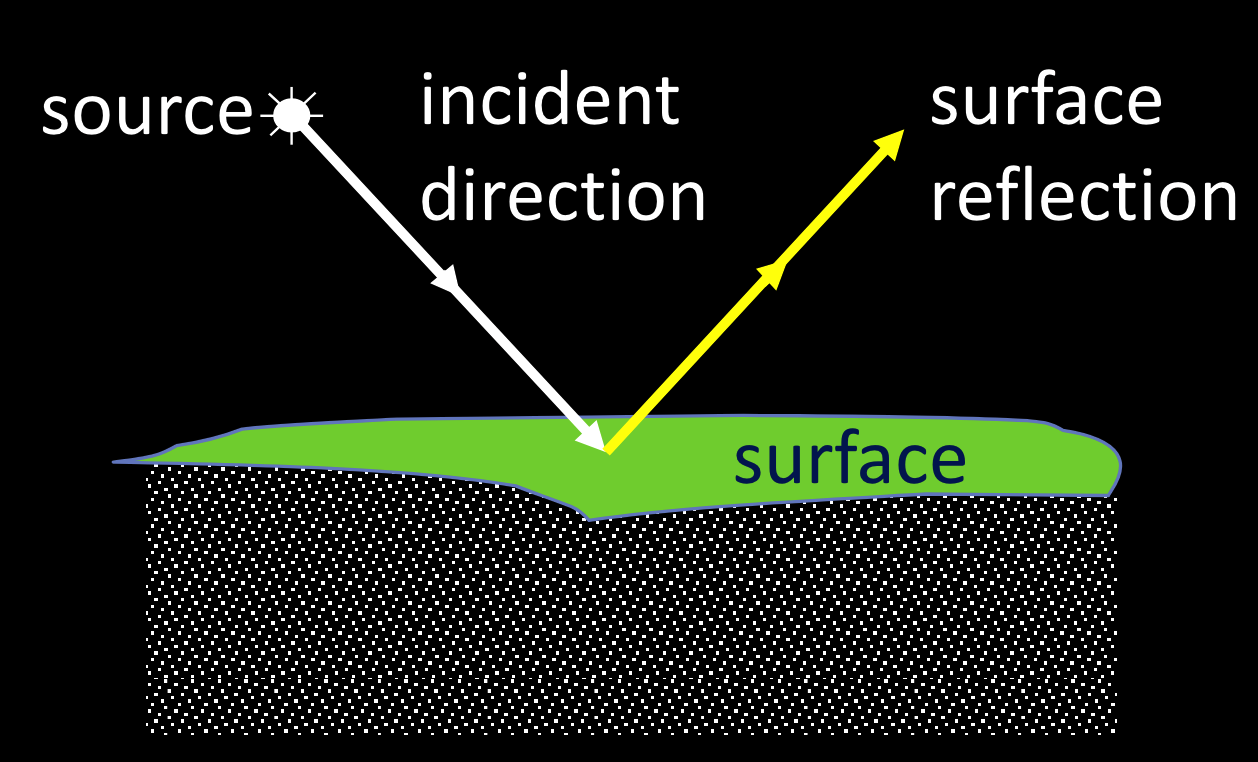
反射光强度

Lambertian BRDF
所有方向看起来一样亮
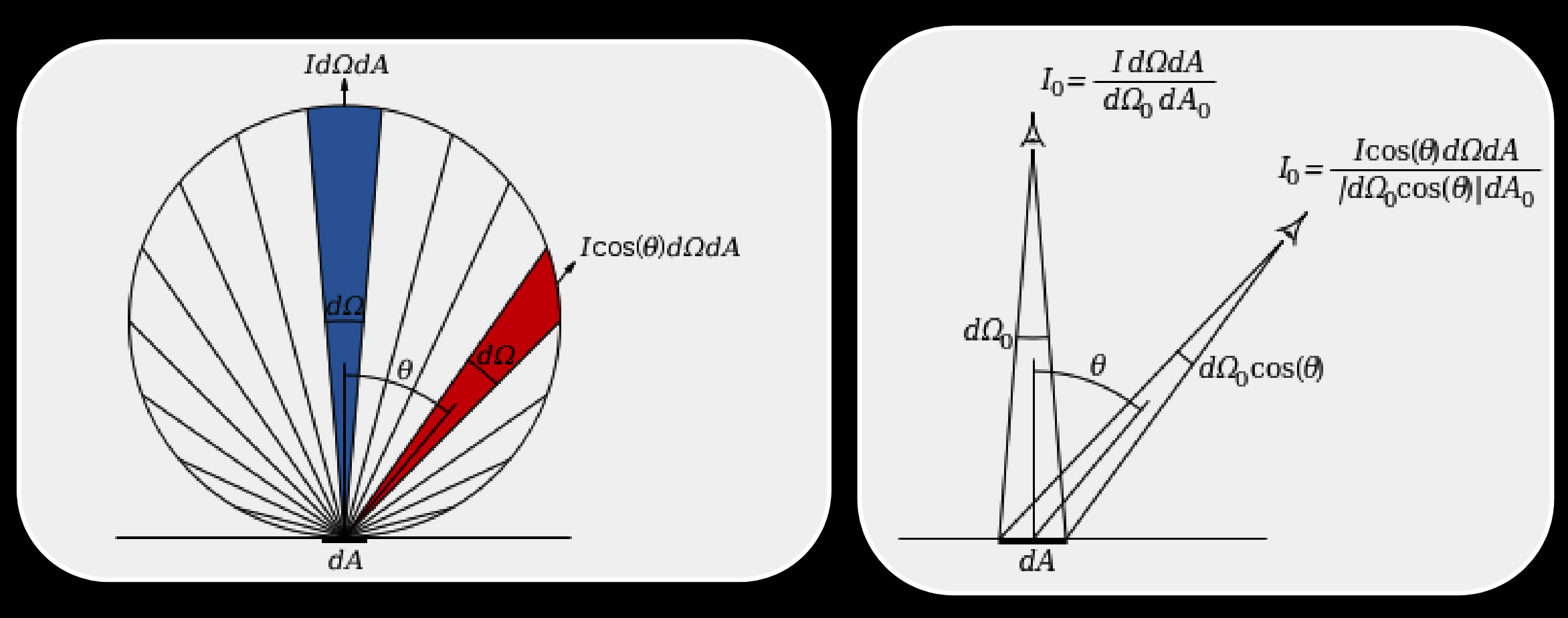
光的反射是按照角度衰减的。
为什么看到的光亮度相同?
因为垂直角度看到的面积小,但亮度高,接近平行的面积大,亮度低,总体看起来亮度相同。
光的反射率是一个常数
$albedo$:$f\left(\theta_i,\varphi_i;\theta_r,\varphi_r\right)=\rho_d$
表面辐射:$L=\rho_d I\cos\theta_i=\rho_d I ( \vec{n} \cdot\vec{s})$
镜面BRDF: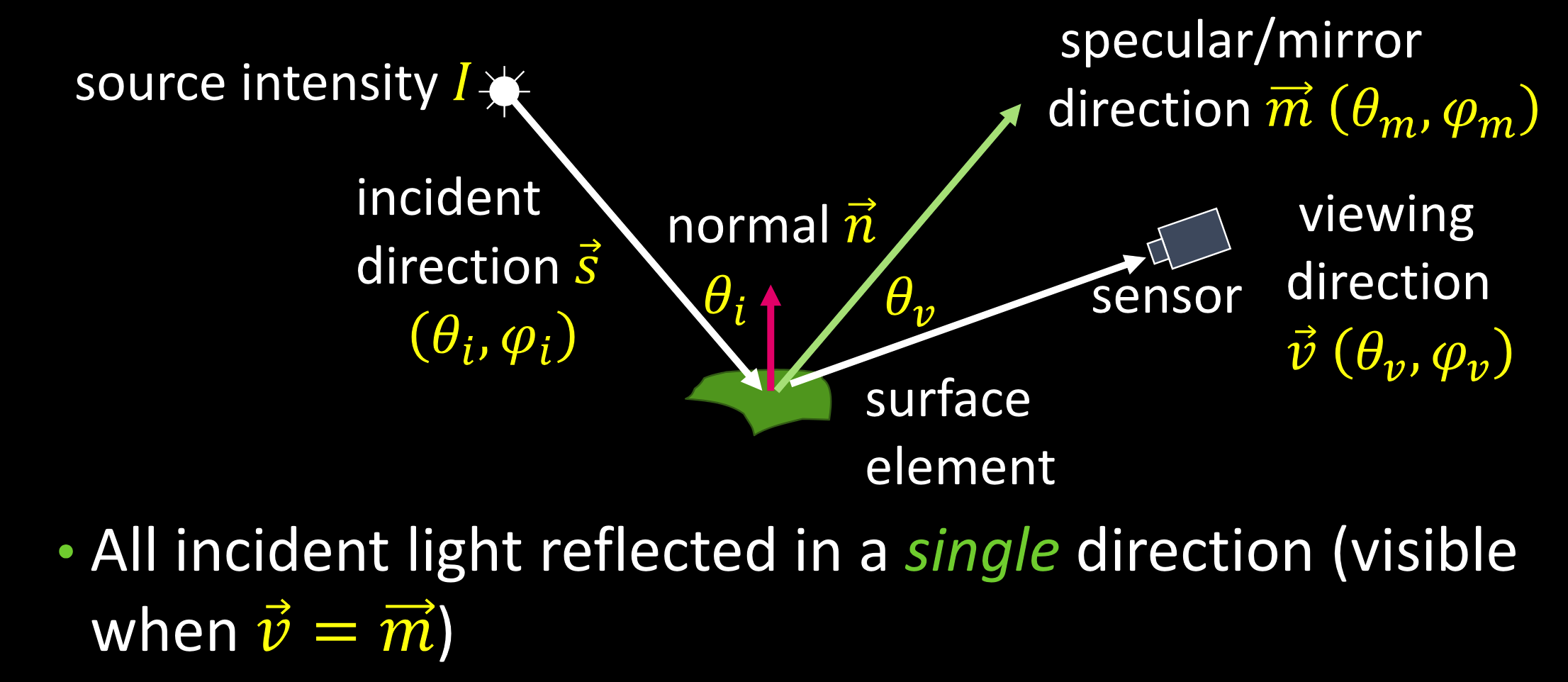
BRDF:$f(\theta_i,\phi_i;\theta_v,\phi_v)=\rho_s\delta(\theta_i-\theta_v)\delta(\phi_i+\pi-\phi_v)$
表面辐射:$L=I\rho_S\delta(\theta_i-\theta_v)\delta(\varphi_i+\pi-\varphi_v)$
另一种写法:$L=I\rho_s\delta(\vec{m}-\vec{v})\mathrm{~or~}I\rho_s\delta(\vec{n}-\vec{h})$
$\vec{h}$:半角
光泽BRDF Glossy
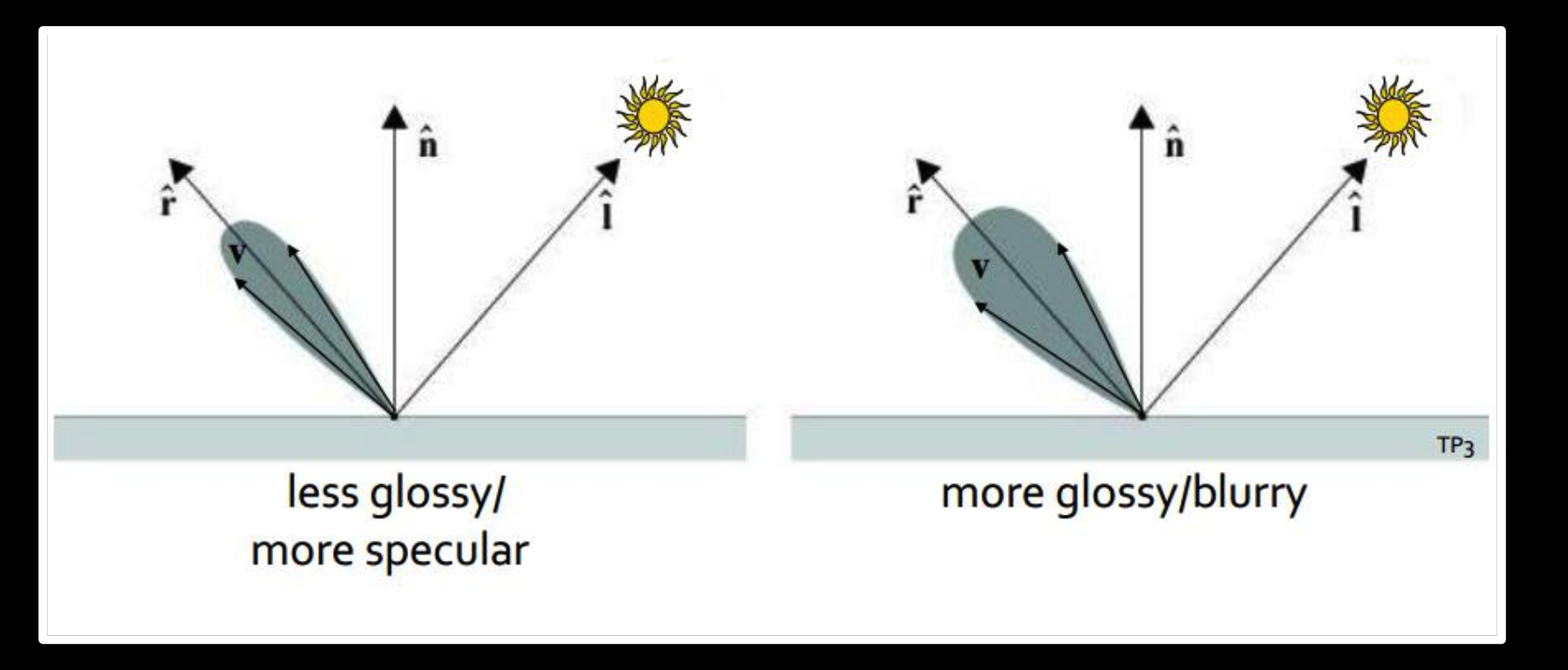
表面辐射:$L=I\rho_s(\vec{m}\cdot\vec{v})^k$
Phong 反射模型

亮度
亮度假设

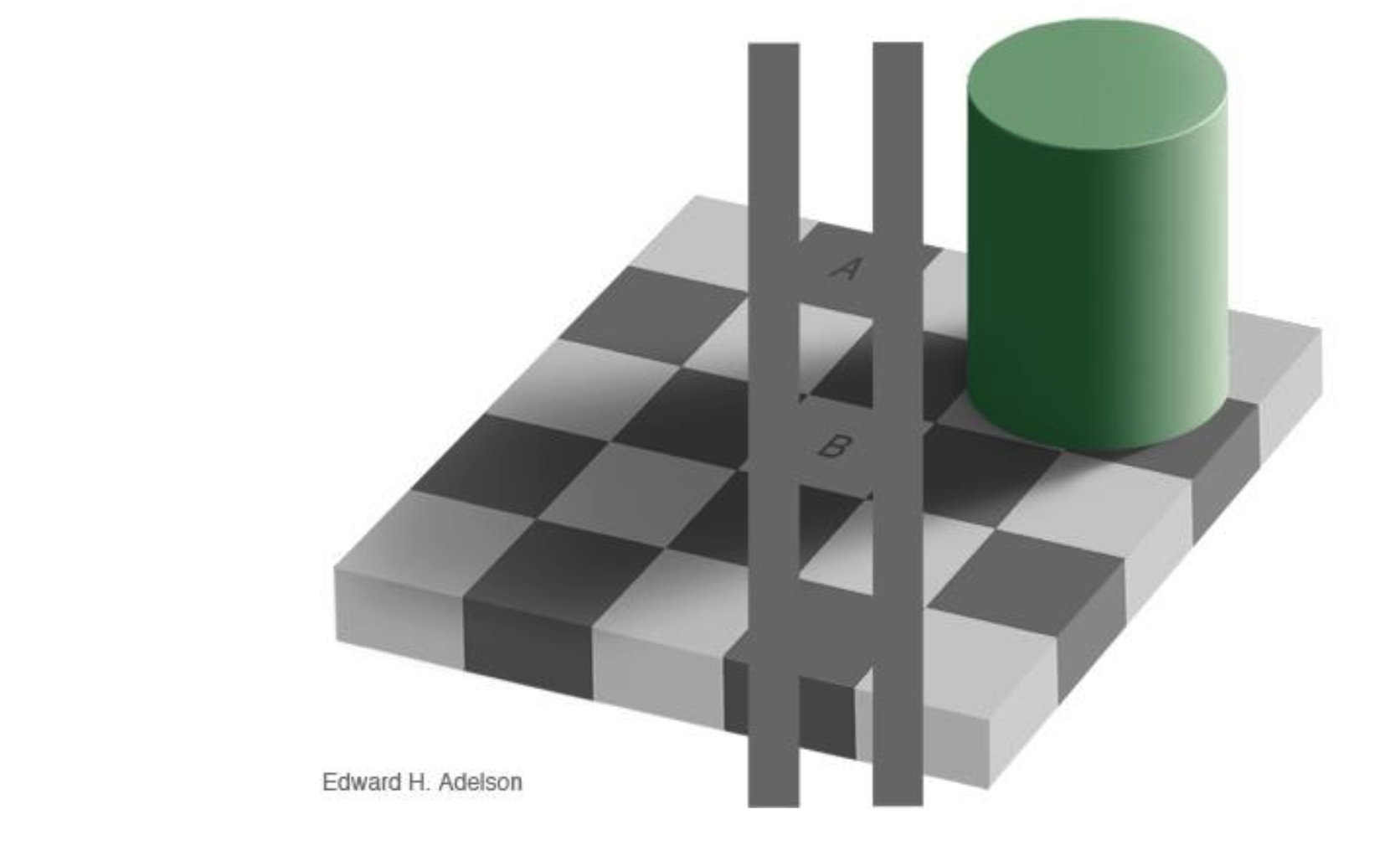
实际上两个方块的亮度是相同的,但大脑一直在补偿阴影。


亮度:等于反射率乘能量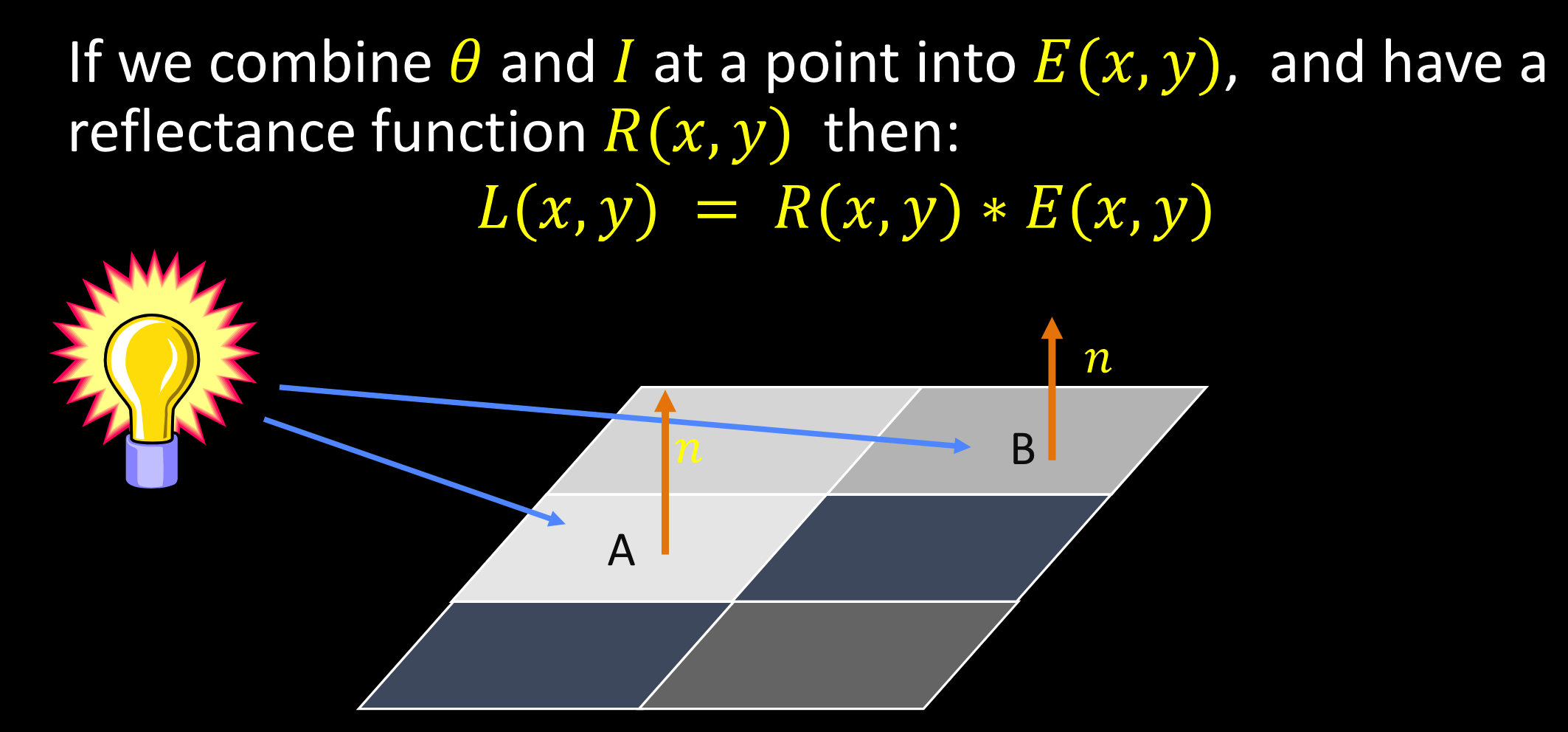
蒙德里安世界 The Mondrian world
计算机的假设:
- 光是缓慢变化的
- 反射率是常数
- 物体之间的反射率变化急剧
强度恒定的斑块: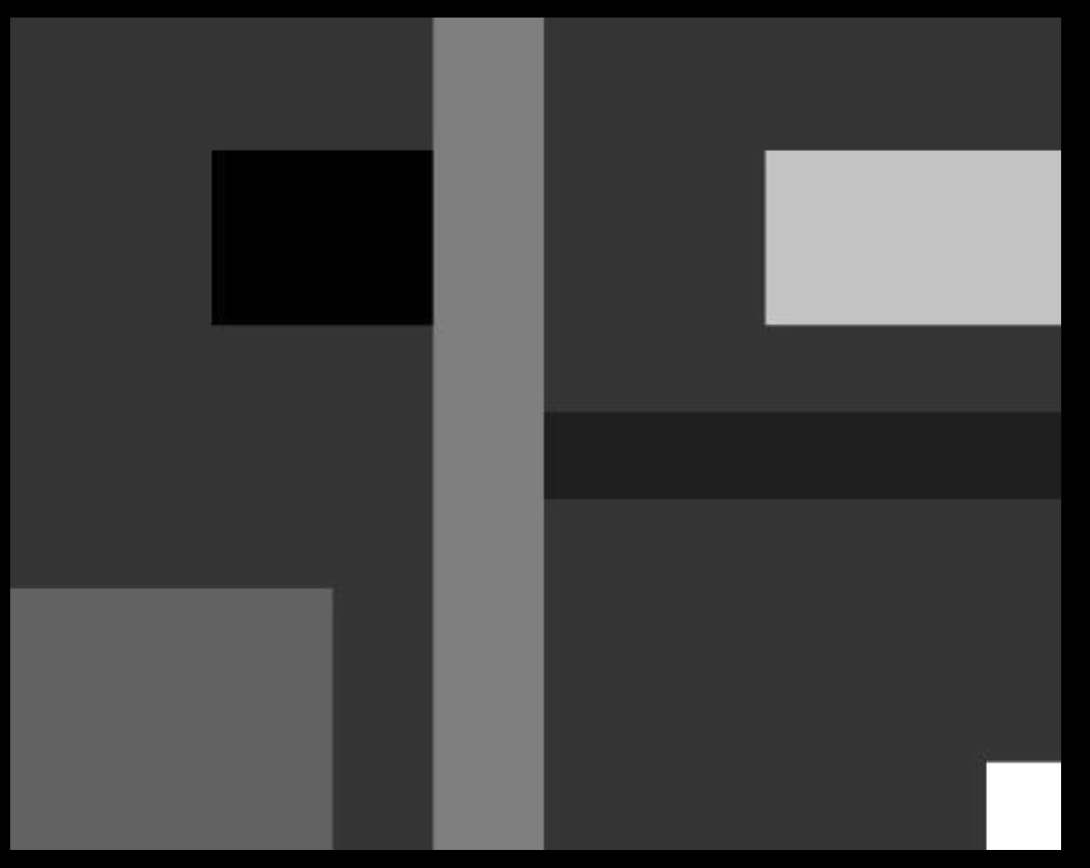
假设光照强度是低频的,缓慢变化。
边缘的反射率是恒定的。
图像相加?: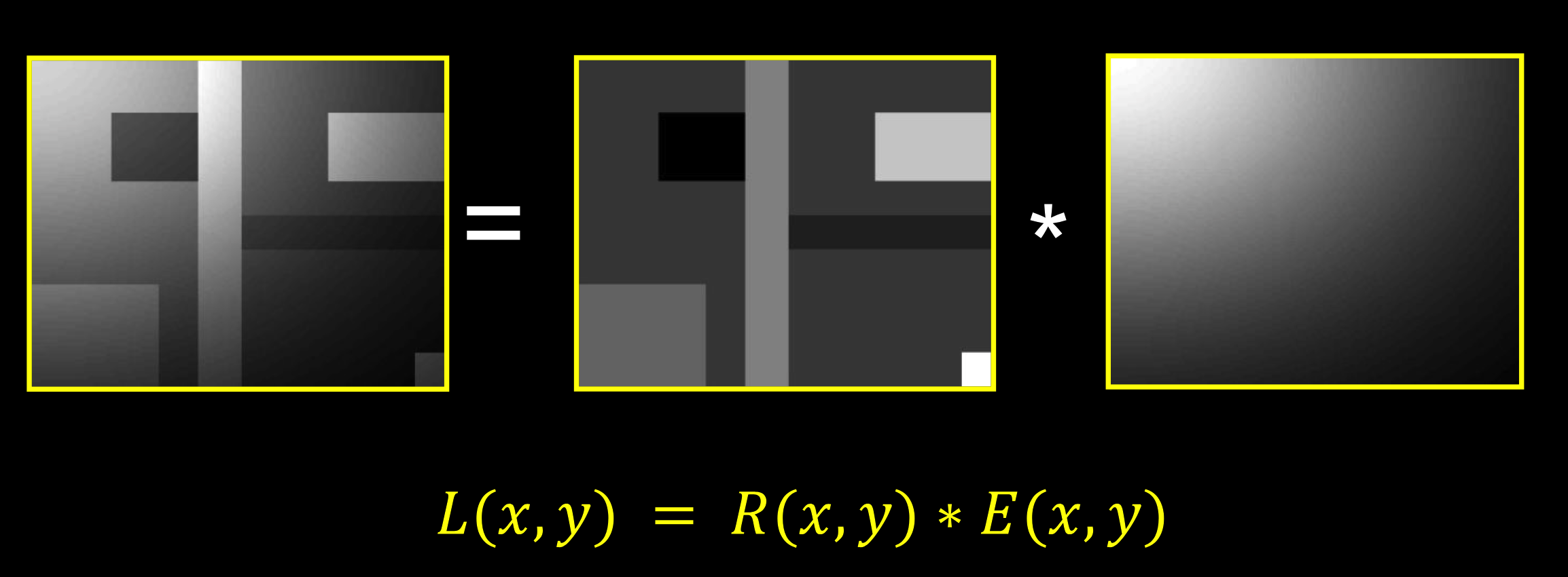
如何恢复反射率: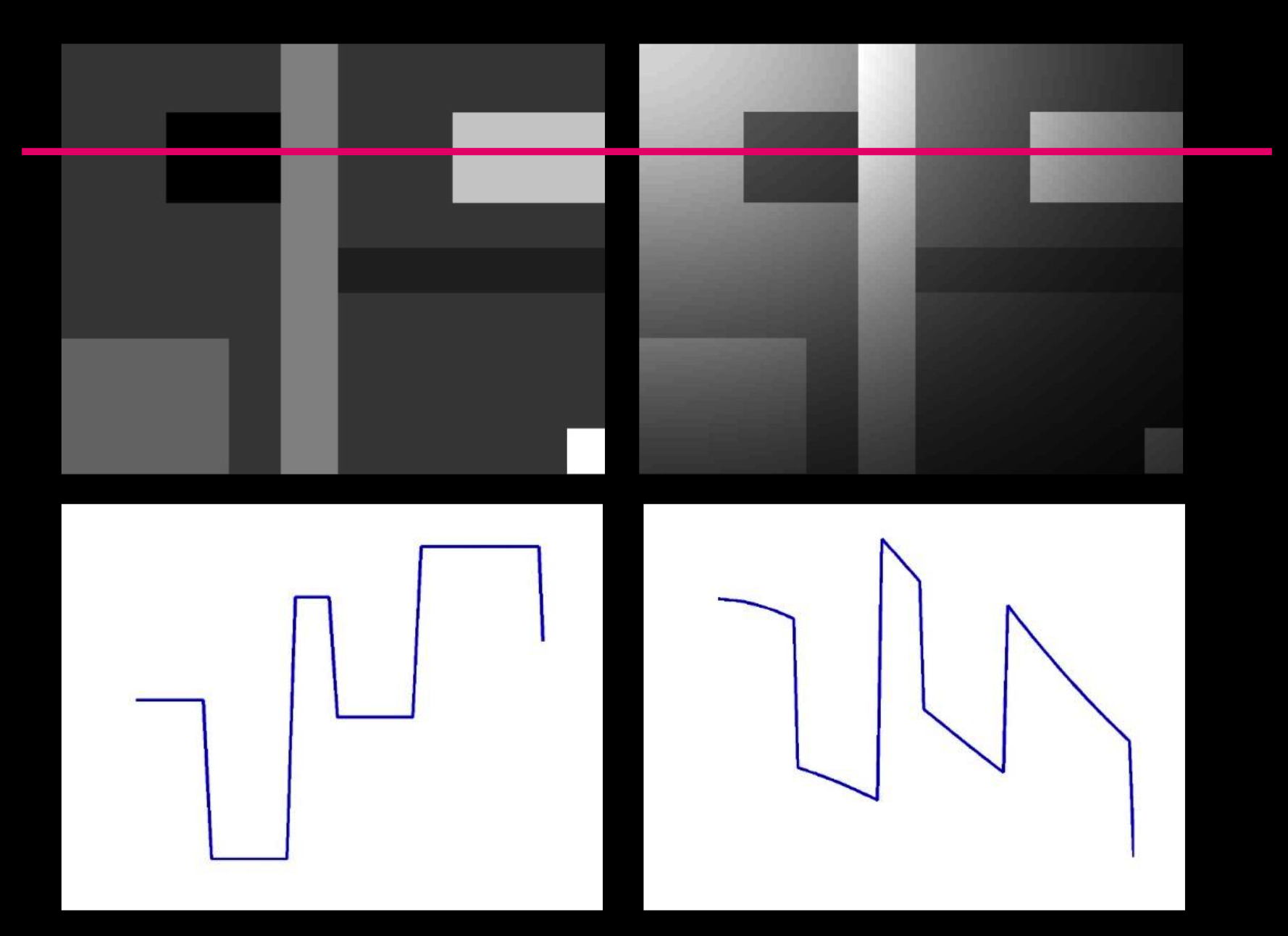
视网膜色素 Land’s Retinex Theory
展示了人类如何感知不同色素
目标:消除缓慢变化
$\log(L(x,y))~=~\log(R(x,y))~+~\log(E(x,y))$
高通滤波保留高波,去掉阀值。
一维亮度: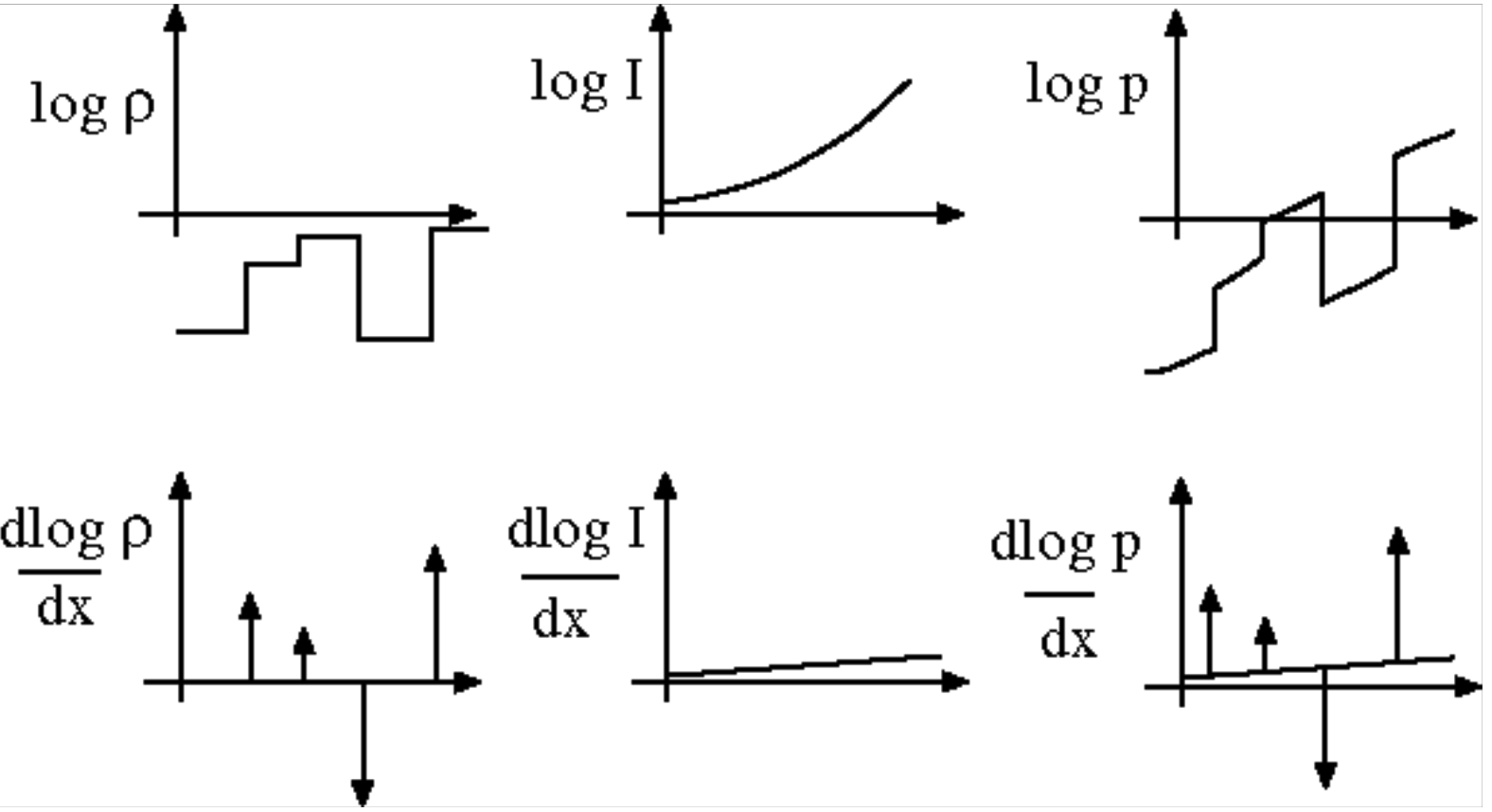
处理阀值,整合成反射率,但是多一个常数。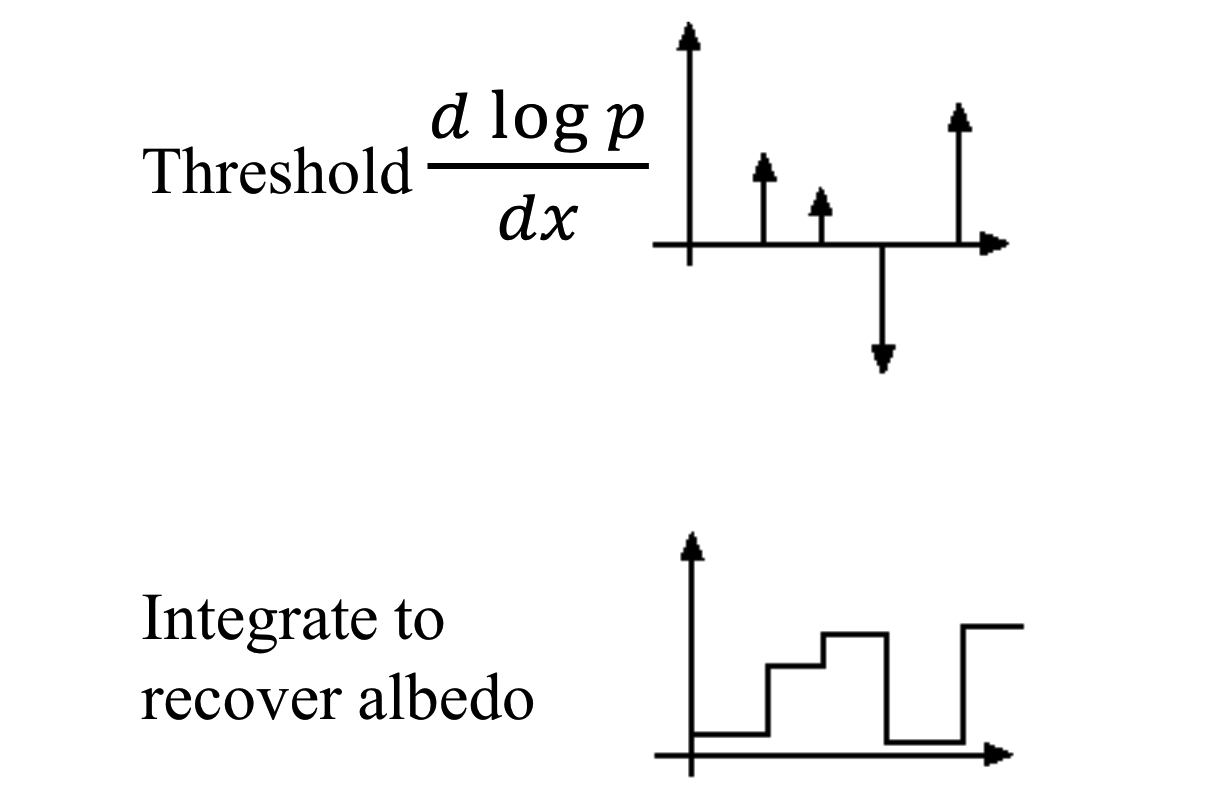
例子:彩色视网膜
重新校准强度
颜色恒定率,强度恒定率
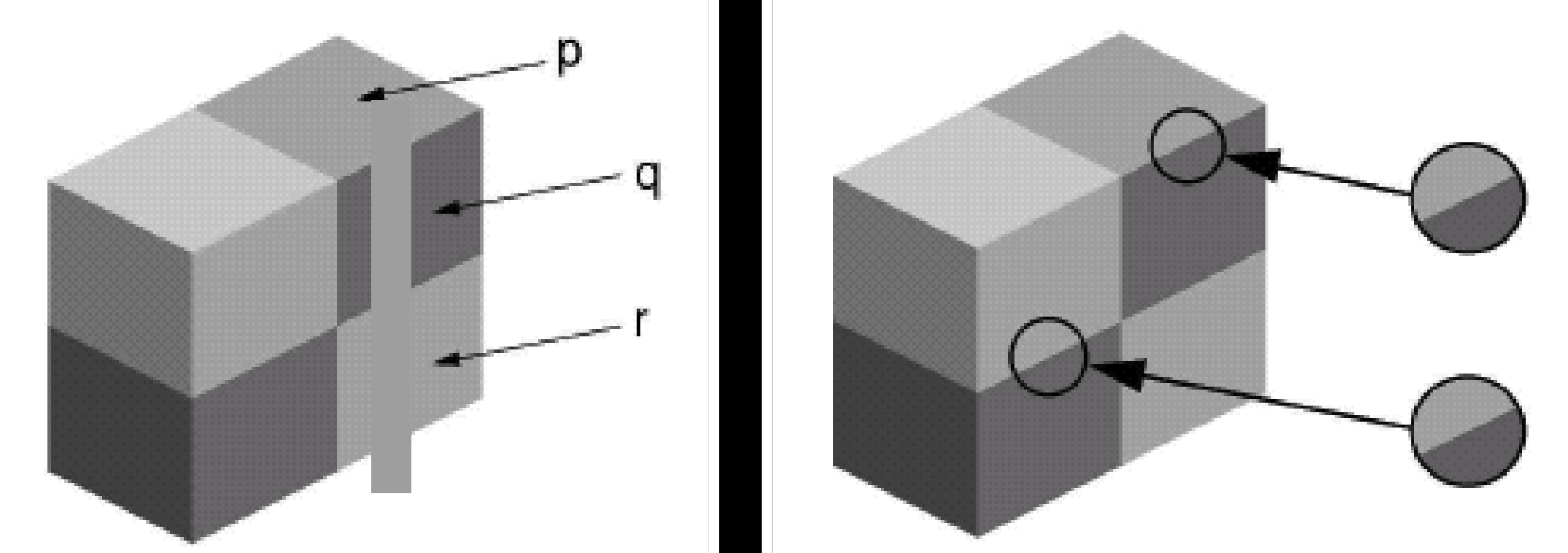
颜色恒定率:某种颜色,在不用光照下,仍然可以看到颜色
强度恒定率:在不同环境,可以感知相同的强度。
阴影
阴影的形状
阴影作为恢复形状的提示
反射率图
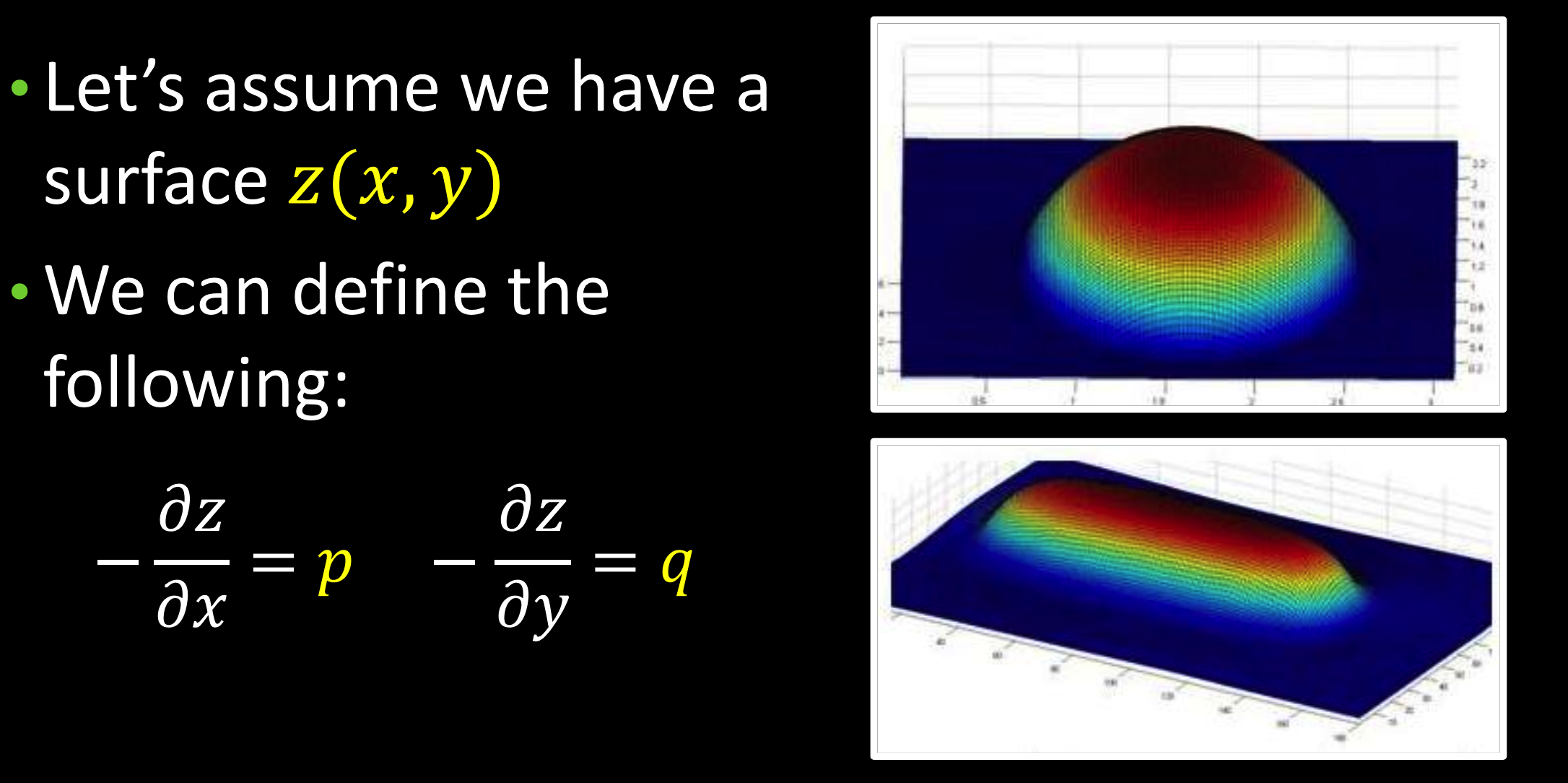
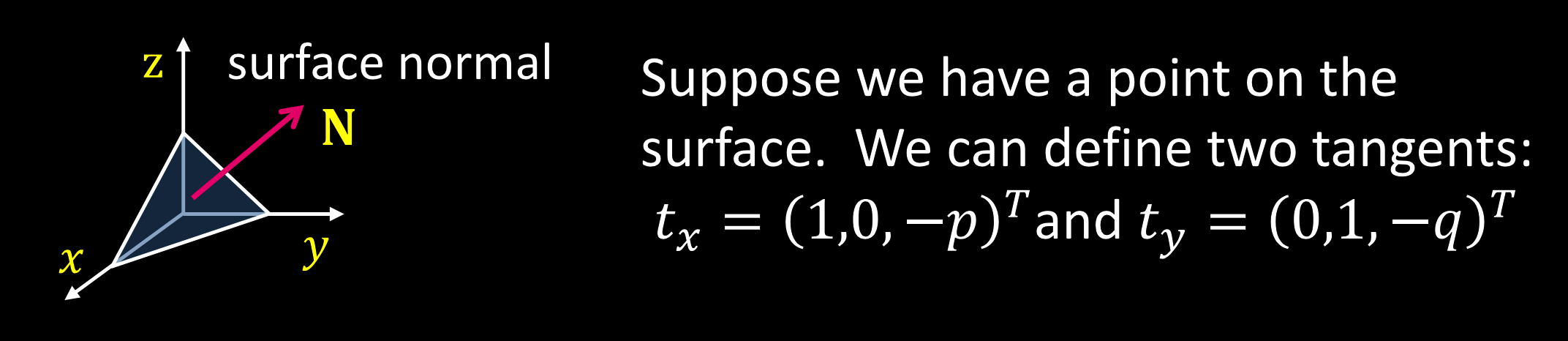
曲线法向量:$\mathbf{n}=\frac N{\left\|N\right\|}=\frac{t_x\times t_y}{\left\|t_x\times t_y\right\|}=\frac1{\sqrt{p^2+q^2+1}}\left(p,q,1\right)^T$
高斯球和梯度空间投影
存在从所有法线到高斯球的映射: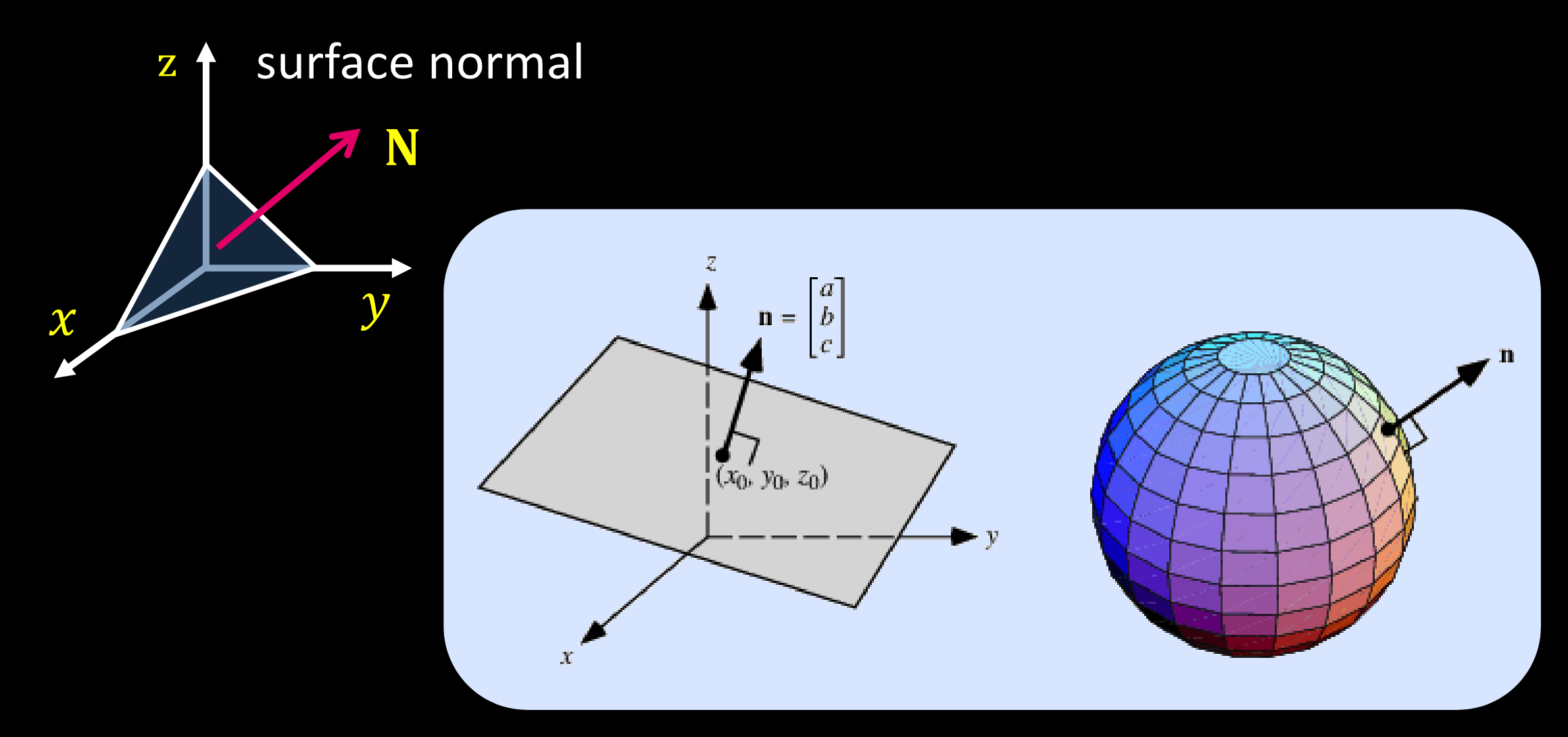
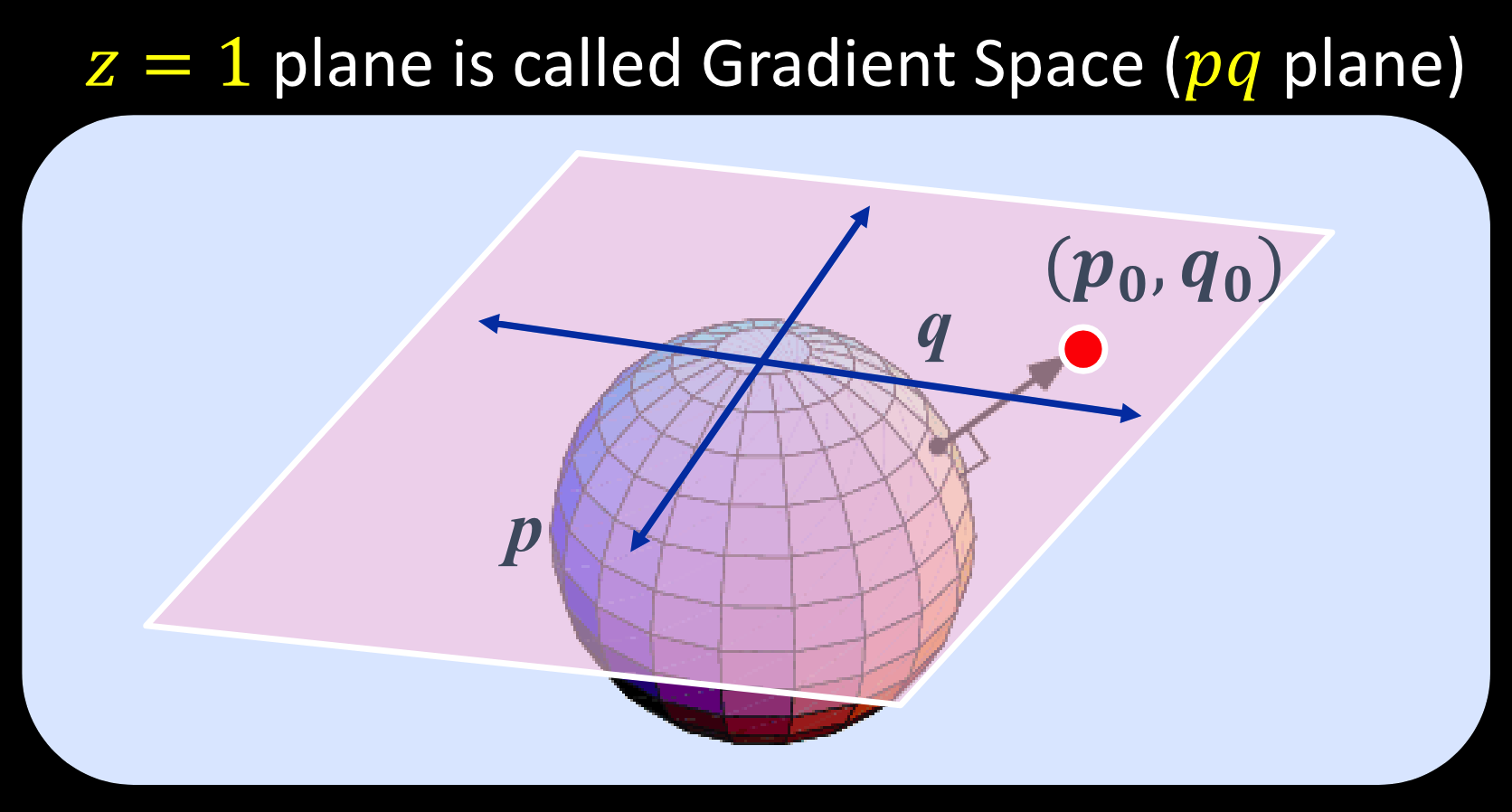
源向量梯度空间和法向量梯度空间
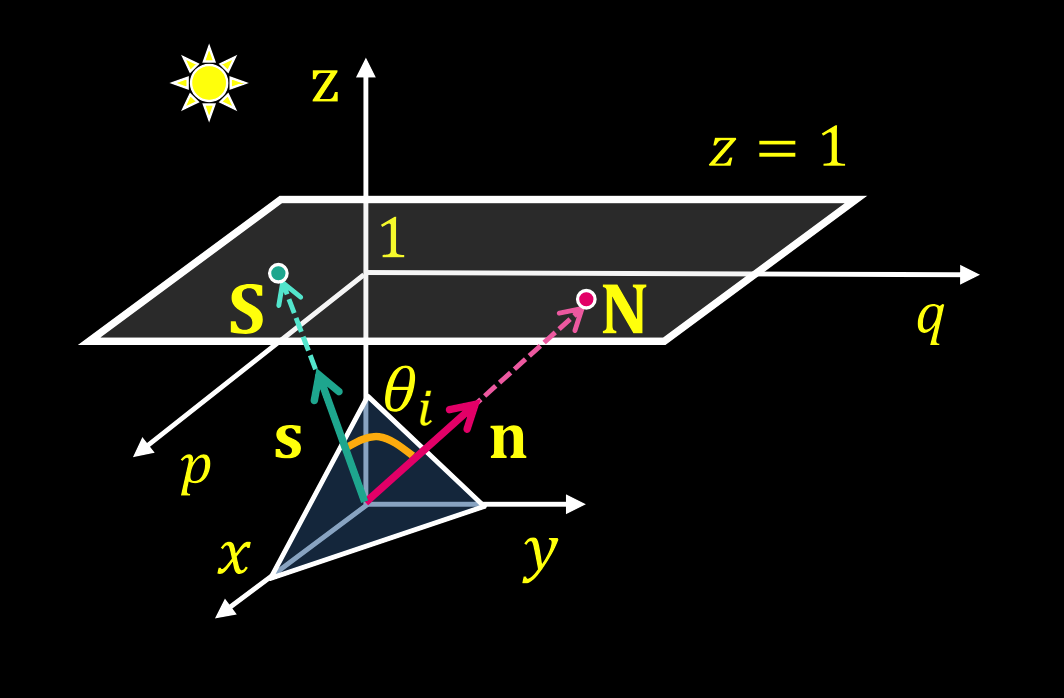
单位法向量:$\mathbf{n=\frac N{|N|}=\frac{(p,q,1)}{\sqrt{p^2+q^2+1}}}$
单位源向量:$\mathbf{s}=\frac{\mathbf{S}}{|\mathbf{S}|}=\frac{(p_S,q_S,1)}{\sqrt{p_S^2+q_S^2+1}}$
向量夹角:$\cos\theta_i=\mathbf{n}\cdot\mathbf{s}=\frac{(pp_S+qq_S+1)}{\sqrt{p^2+q^2+1}\sqrt{p_S^2+q_S^2+1}}$
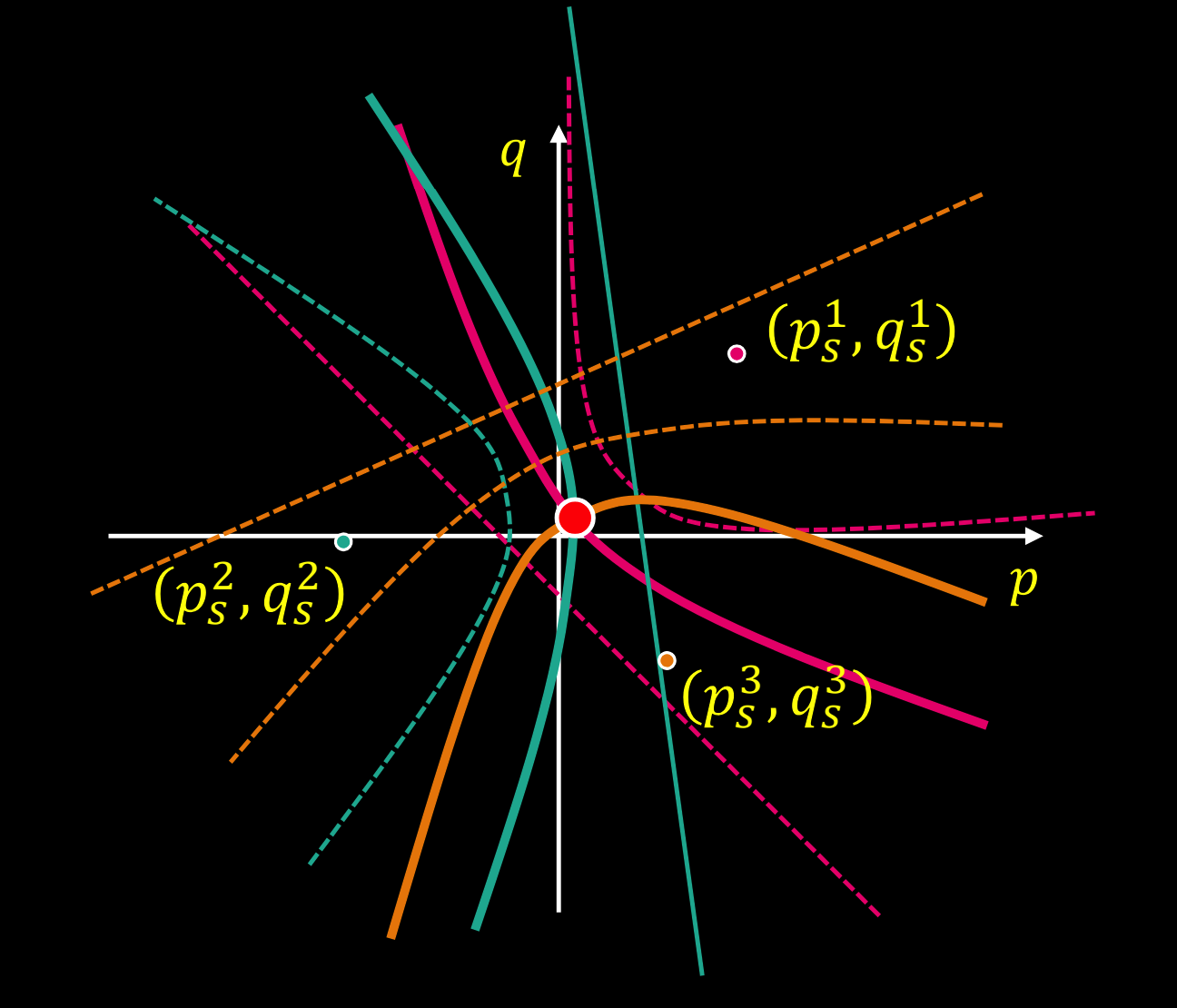
阴影形状的定义
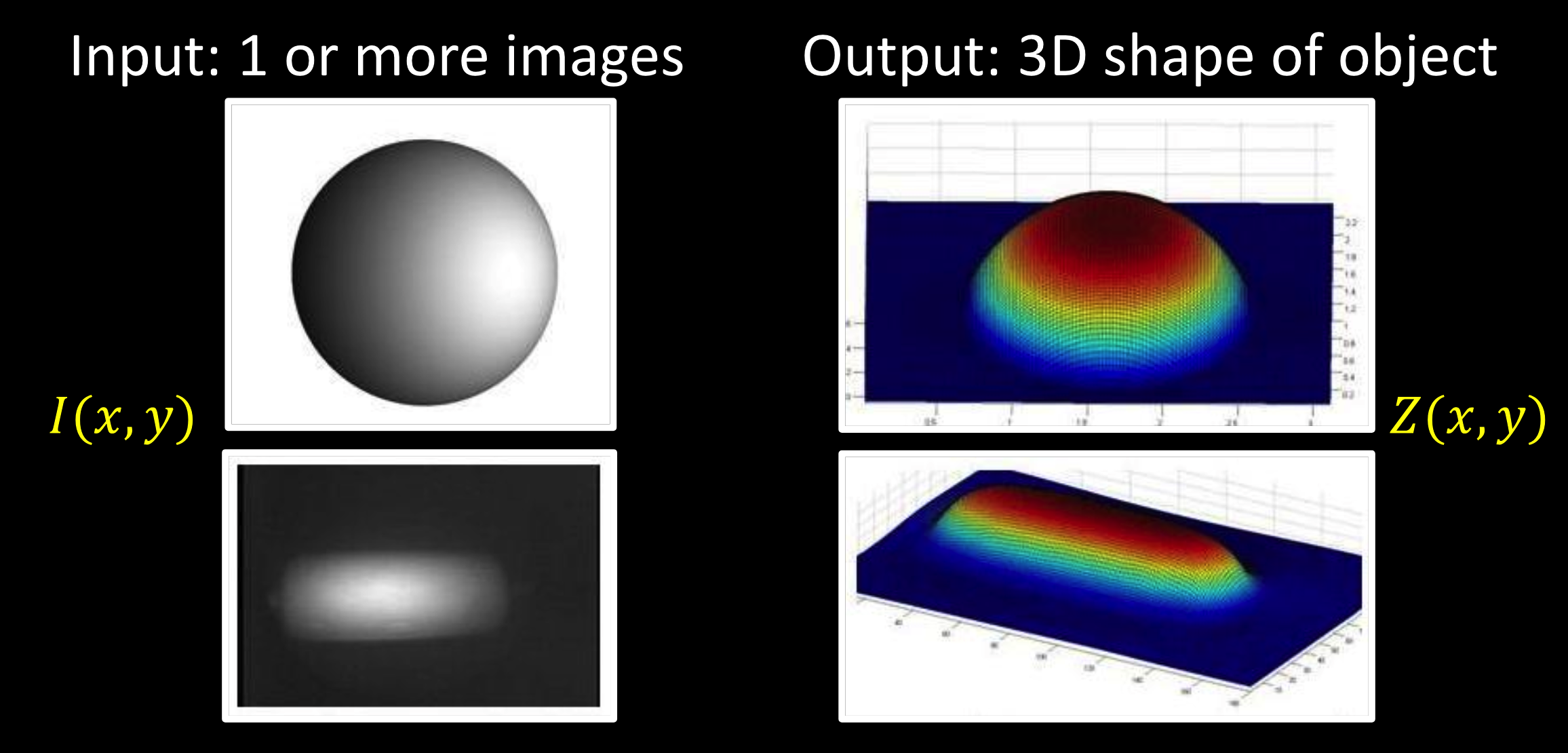
朗伯案例

反射图: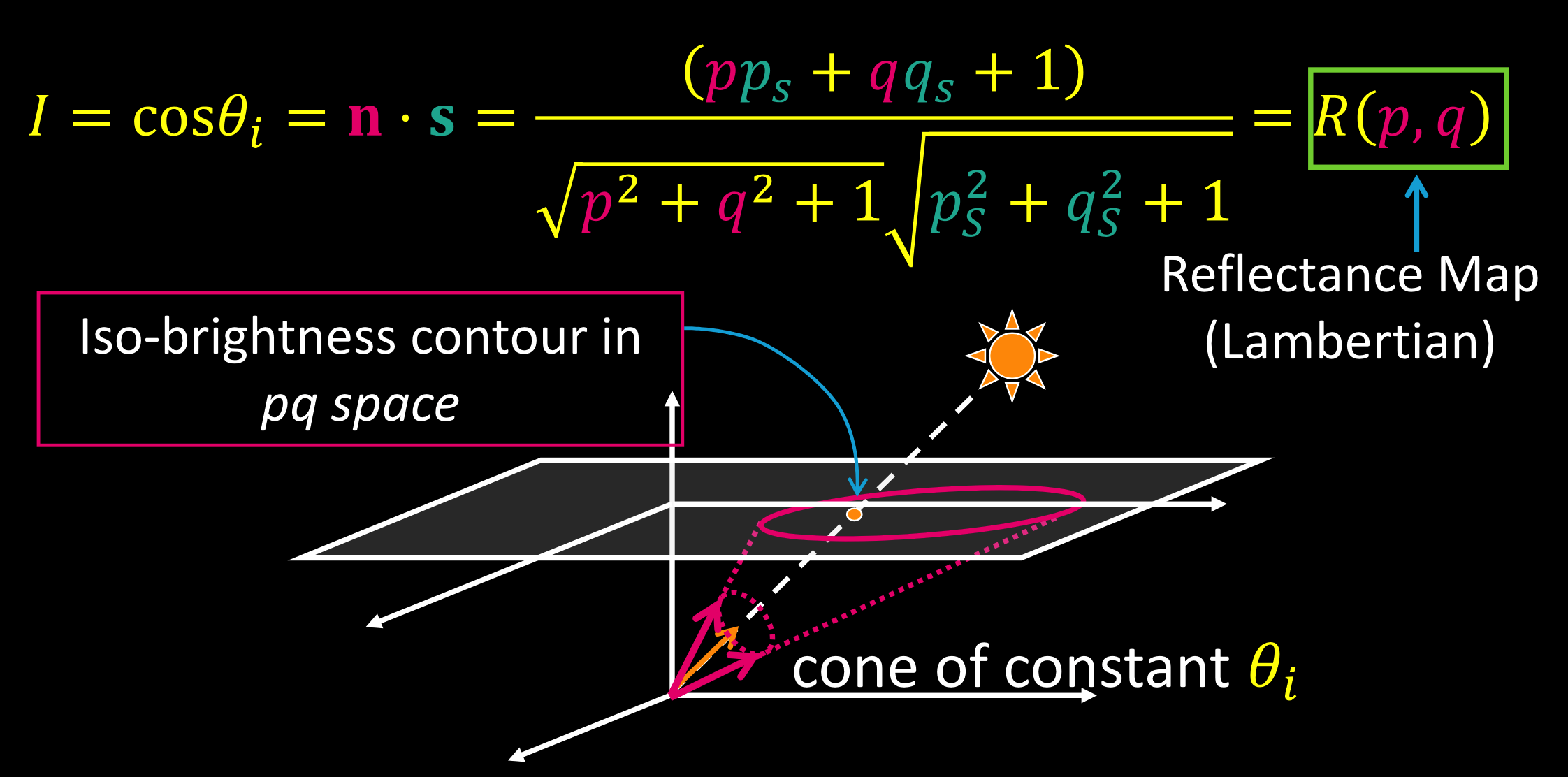
Iso 亮度轮廓:
光度立体
相同的物体,不同的光照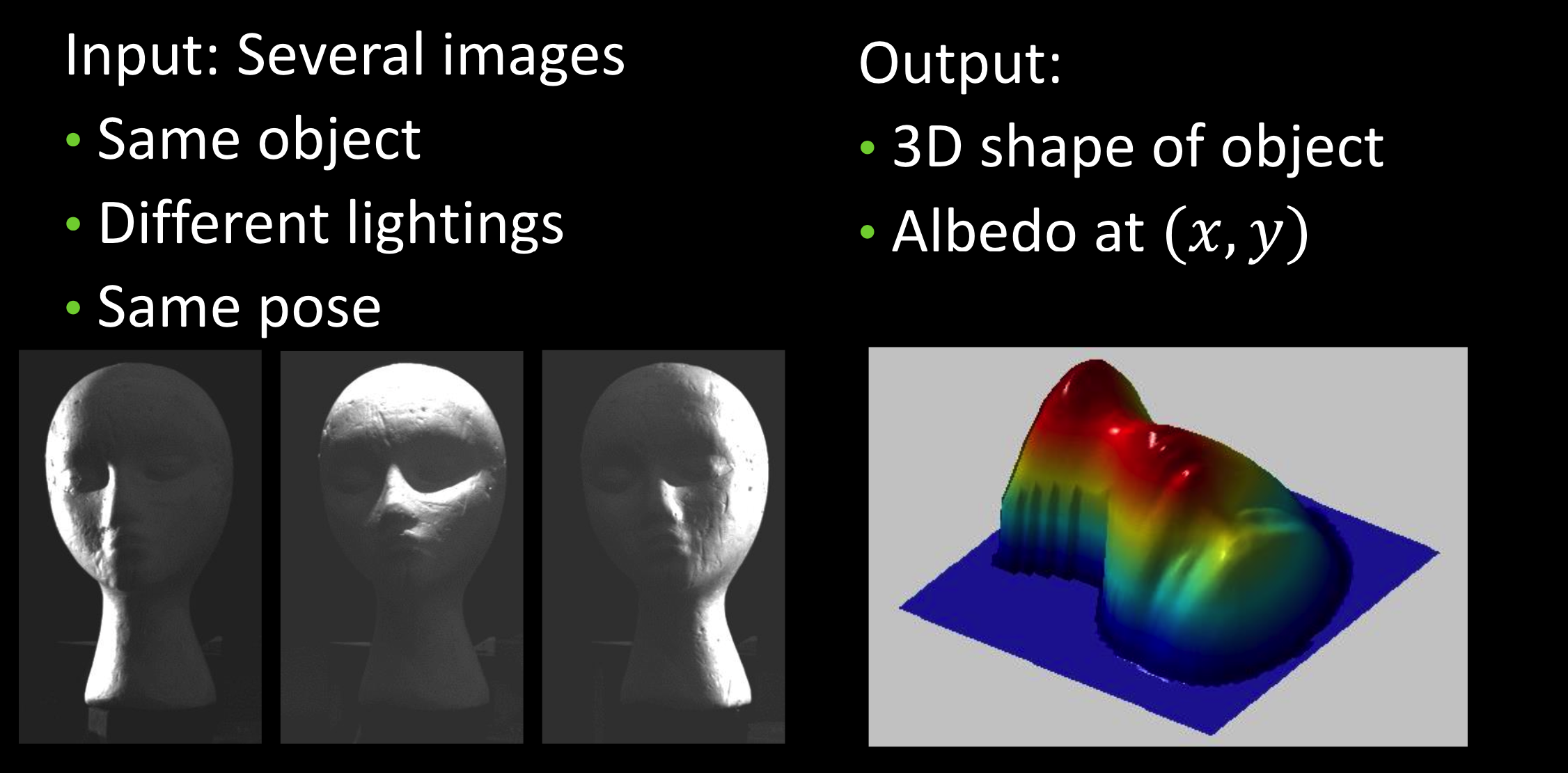



最终pq空间图: