计算机视觉概论 图像特征
更新历史
- 24.05.02:初稿
系列
特征检测
一种寻找对应关系的方法
图像点匹配问题
Local Features:局部特征
目标:在其他图像中找到点的精确位置
特征匹配的过程:
- 检测一些兴趣点(特征)
- 匹配两张图中的特征点
- 使用对应点,对齐图像
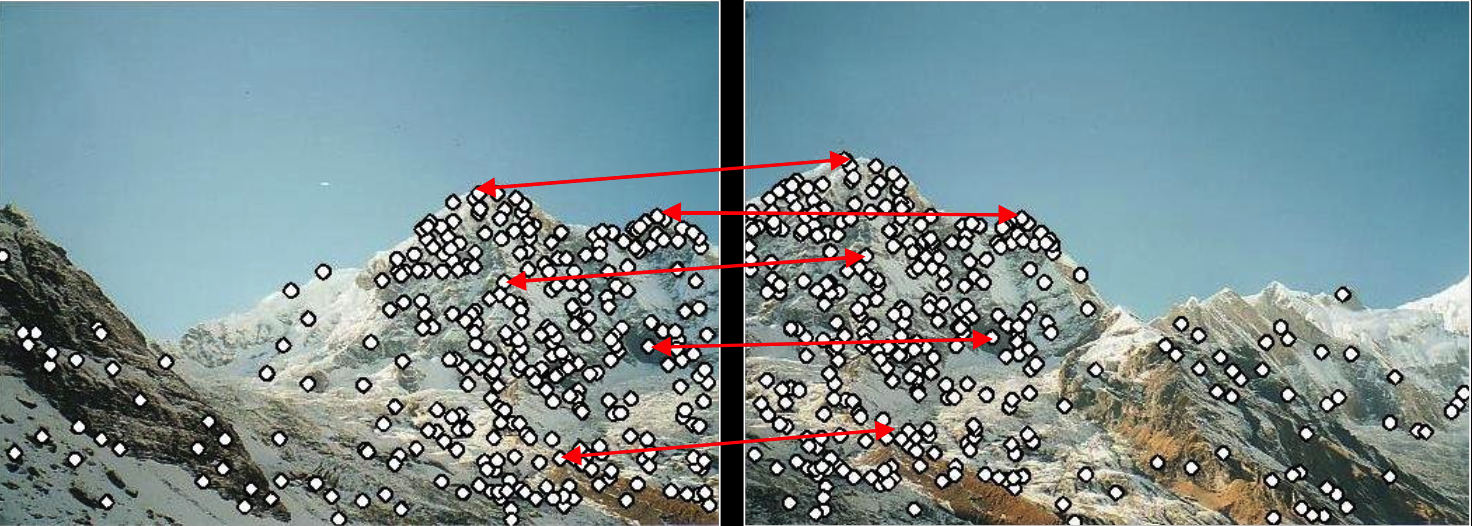
特征匹配的问题:
- 独立的特征, 需要重复检测器
- 重复相似匹配,使用特征描述符descriptor
好的特征
可重复性:Repeatability/Precision
好的特征应该在同一场景的不同图片中被检测出来
显著性/可匹配性:Saliency/Matchability
有不同的区分描述
紧凑型和效率:Compactness and efficiency
比图像像素更少的特征
局部性:Locality
描述具有好的局部性,可以解决遮挡
寻找角点
一个白墙上有一个黑色方块:
黑块不是一个好特征,无法定位。
边缘也不是好特征,角是一个好特征。

角是一个梯度变换的地方。
哈里斯角 Harris Corners:
$E\left(u,\nu\right)=\sum_{x,y}w\left(x,y\right)\left[I\left(x+u,y+\nu\right)-I\left(x,y\right)\right]^{2}$
- $w\left(x,y\right)$ 是一个窗口

哈里斯角图:
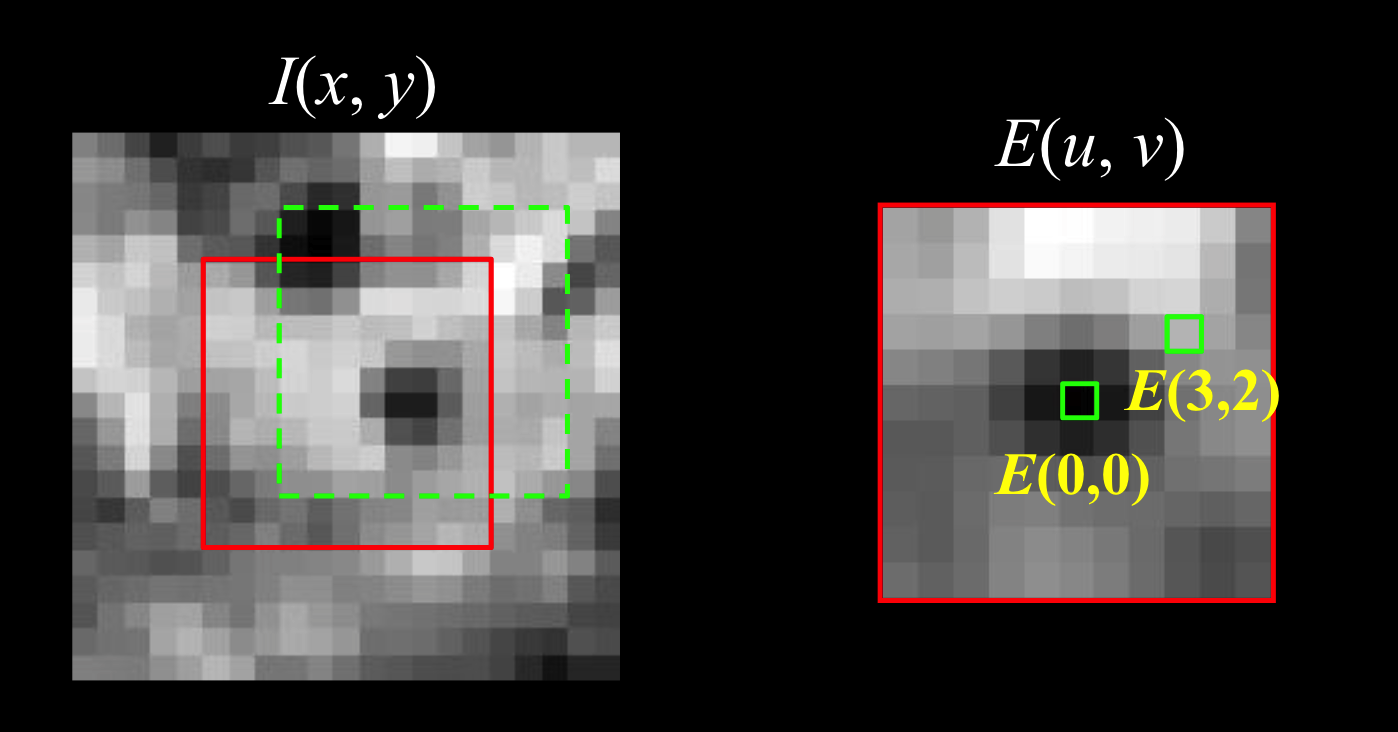
- 误差为0,是黑色
- 左图中红色方块是角图中心,误差为0,绿色移动后,出现误差
哈里斯角在很小的移动会产生误差:
二阶泰勒展开:
$F\left(\delta x\right)\approx F\left(0\right)+\delta x\cdot\frac{dF\left(0\right)}{dx}+\frac12\delta x^2\cdot\frac{d^2F\left(0\right)}{dx^2}$
二维泰勒展开: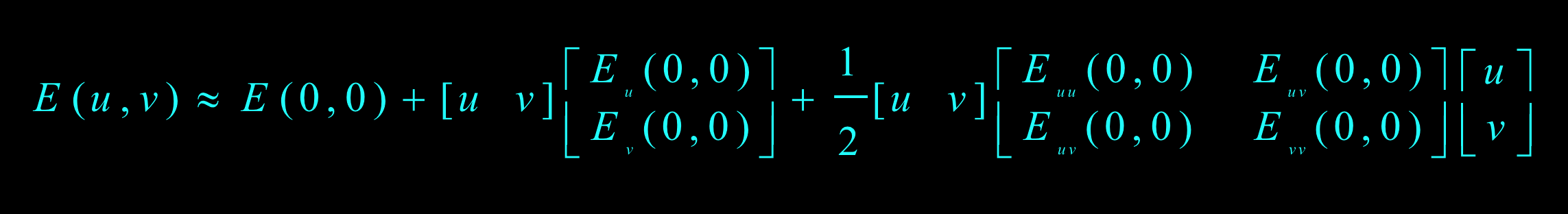
推导过程:
$E_u\left(u,\nu\right)=\sum_{x,y}2w\left(x,y\right)\left[I\left(x+u,y+\nu\right)-I\left(x,y\right)\right]I_x\left(x+u,y+v\right)$
$\begin{split}
E_{\textit{ u }\nu}\left(u,\nu\right)& =\sum_{x,y}2w(x,y)I_y(x+u,y+v)I_x(x+u,y+v) \\
&+\sum_{x,y}2w(x,y)\Big[I(x+u,y+v)-I(x,y)\Big]I_{xy}(x+u,y+v)
\end{split}$
$\begin{split}E_{u\nu}(u,\nu)&=\sum_{x,y}2w(x,y)I_y(x+u,y+v)I_x(x+u,y+v)\\&+\sum_{x,y}2w(x,y)\Big[I(x+u,y+v)-I(x,y)\Big]I_{xy}(x+u,y+v)\end{split}$
带入点$(0,0)$,消去得:
$E\left(u ,\nu\right) \approx \begin{bmatrix}u&\nu\end{bmatrix} M\quad\begin{bmatrix}u\\\nu\end{bmatrix}$
$M=\sum_{x,y}w(x,y)\begin{bmatrix}I_x^2&&I_xI_y\\I_xI_y&&I_y^2\end{bmatrix}$
当没有权重$w(x,y)$时:
$M=\begin{bmatrix}\sum I_xI_x&\sum I_xI_y\\\sum I_xI_y&\sum I_yI_y\end{bmatrix}=\sum\left(\begin{bmatrix}I_x\\I_y\end{bmatrix}-\begin{bmatrix}I_x&I_y\end{bmatrix}\right)=\sum\nabla I\left(\nabla I\right)^T$
其中$\nabla I$:是一个秩为1的列向量,所有等式右边是一个秩为1的二阶方阵。
? 必须让窗口内所有方向都有梯度,才可以求和后得到一个满秩矩阵??
解释二阶近似方程
代数表达式:椭圆方程
$\sum I_x^2u^2+2\sum I_xI_yu\nu+\sum I_y^2\nu^2=k$
椭圆图: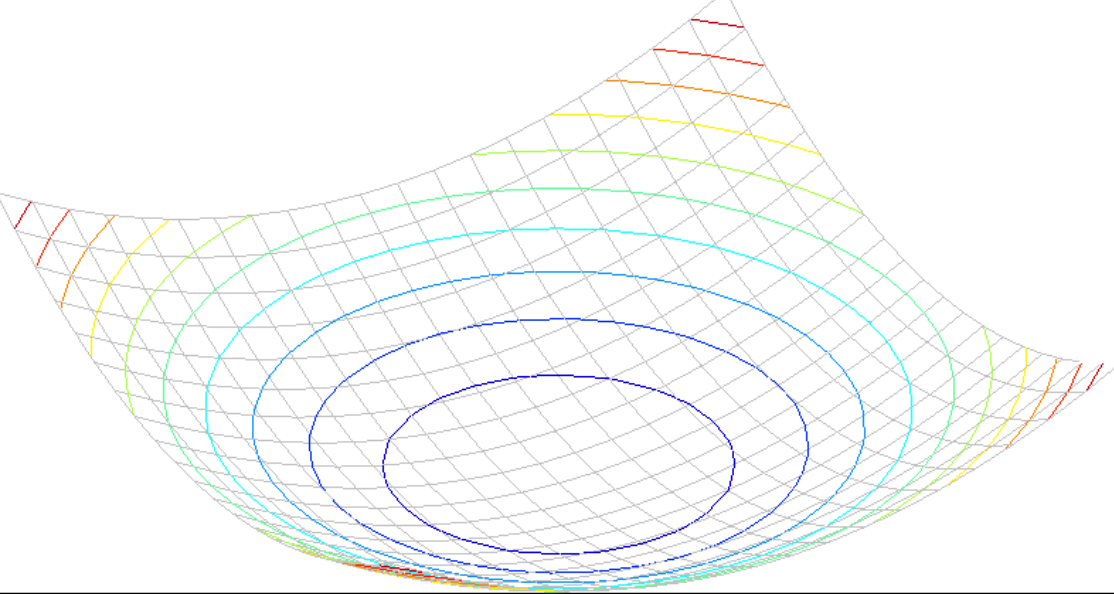
考虑,窗口内的梯度永远是水平或垂直,所有$I_xI_y$为0。
化简:
$M=\sum_{x,y}w(x,y)\begin{bmatrix}I_x^2&&I_xI_y\\I_xI_y&&I_y^2\end{bmatrix}=\begin{bmatrix}\lambda&0\\0&\lambda_2\end{bmatrix}$
$M$可以被相似对角化:
$M~=~R^{-1}\left[\begin{array}{cc}\lambda&0\\0&\lambda_2\end{array}\right]R$
特征值的作用: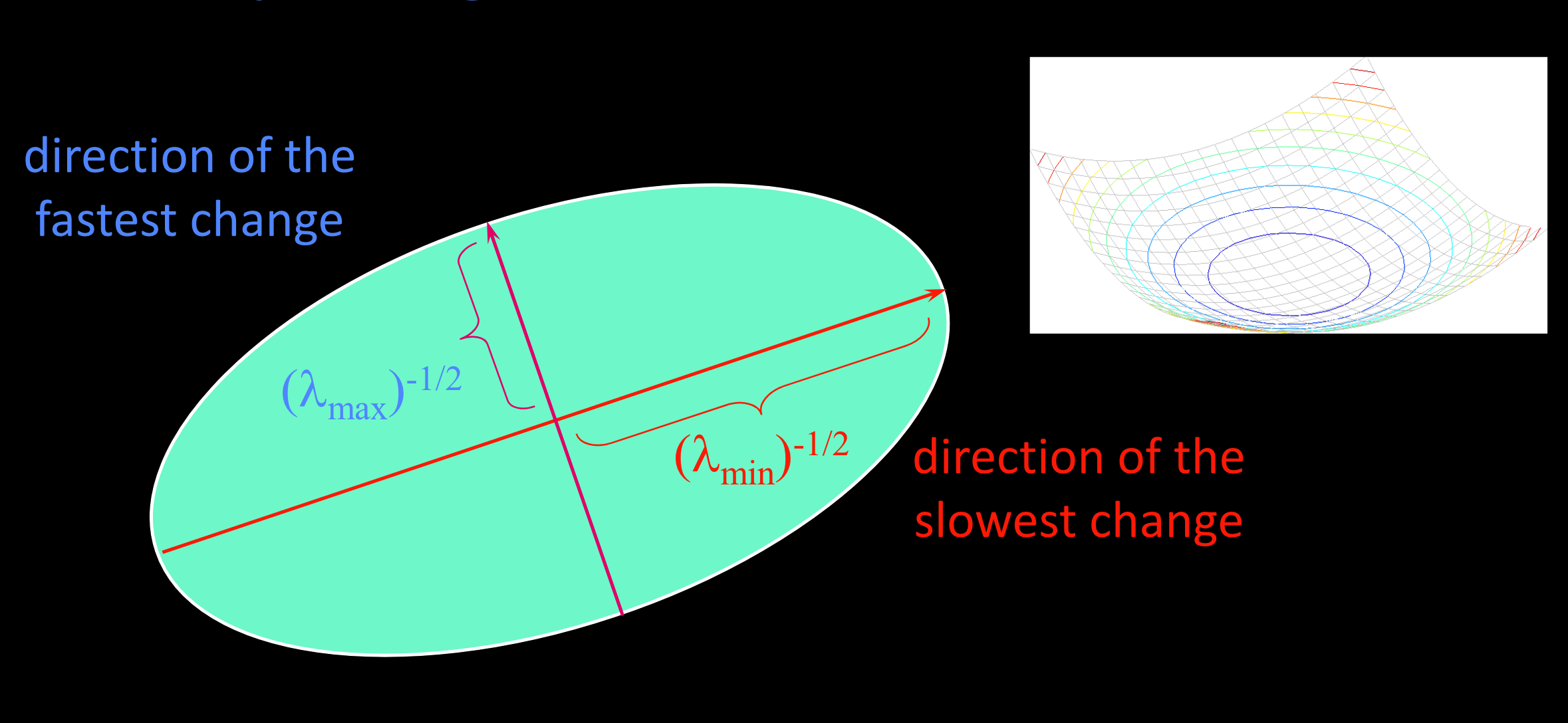
在短边处:变换很快,长边处变换速度很慢,需要移动很多才有变化。
解释特征值
计算哈里斯矩阵: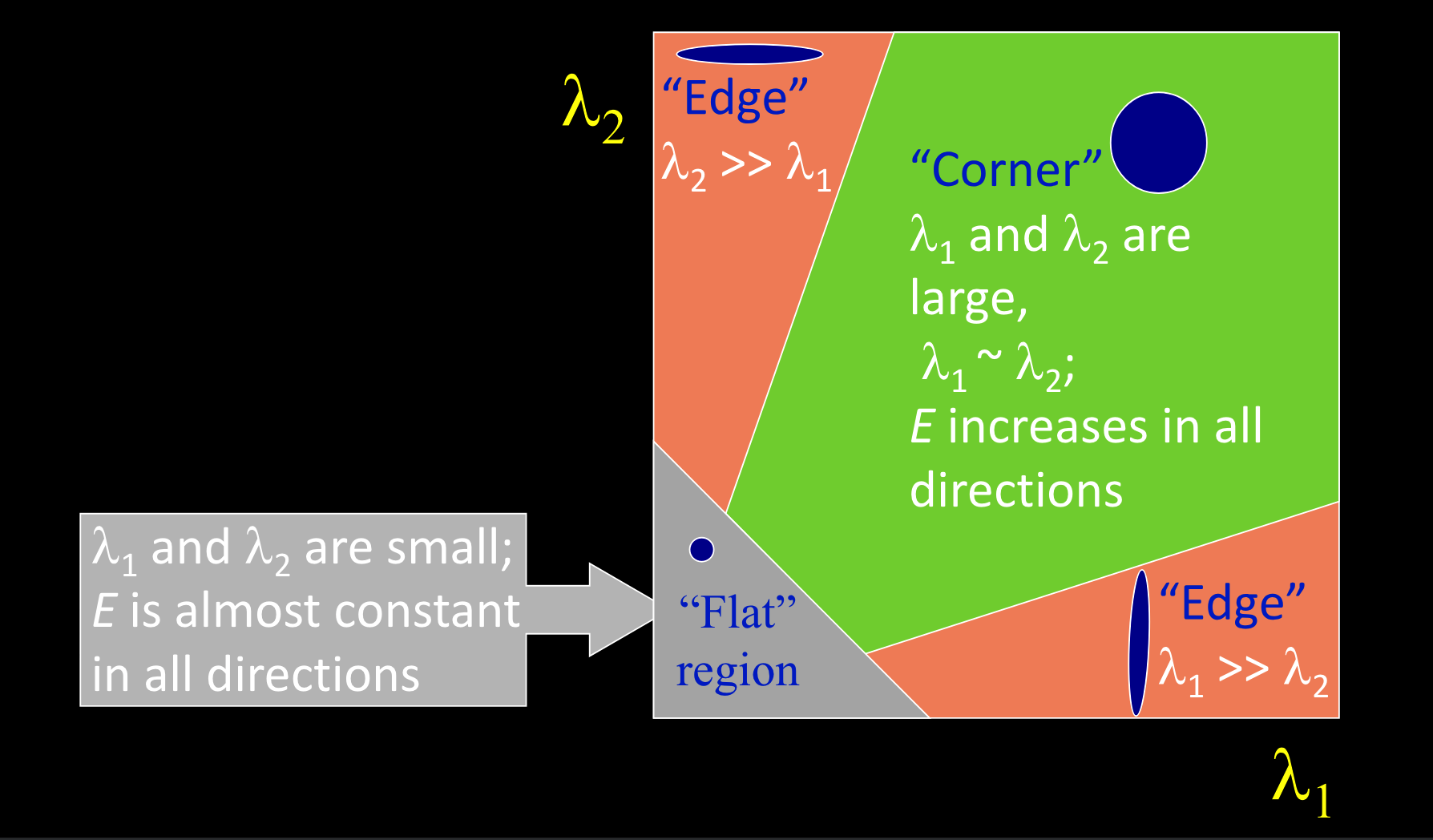
- 平坦区域:flat
梯度为0,怎么移动都不会变化。 - 如果一个特征值特别大
朝这个方向的边缘移动,变换很快 - 两个特征值大小相似
角:在任何方向变化相同
哈里斯响应函数:
$R=\det(M^2)-\alpha\mathrm{~trace}(M)^2=\lambda_1\lambda_2-\alpha(\lambda_1+\lambda_2)^2$
$\alpha$:特别小 0.04 to 0.06
$R$取决于特征值,但不需要计算特征值,
原因:
- 角:两个特征值都很大,$R$正的大数
- 边:一个特征值很大,$R$是负的大数
- 平坦:$R$ 的绝对值很小
哈里斯函数如何工作
低纹理区域:
边缘区域:
高纹理区域:
哈里斯检测器算法:

例子:
响应函数图: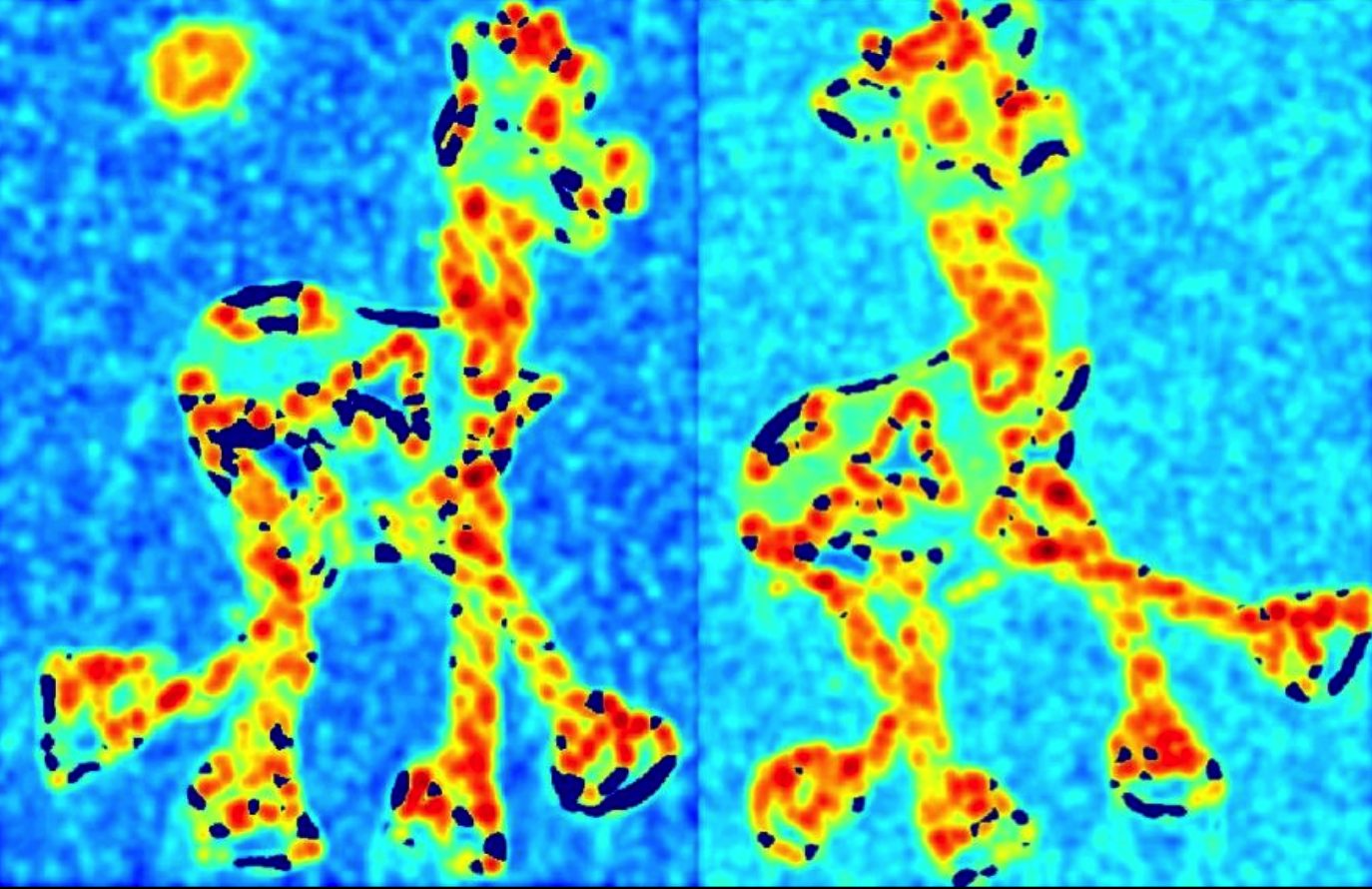
非极大值抑制:
局部最大值的像素点:
在原图中的位置:
最终发现很多相同的特征点。
尺度不变性 Scale invariance
哈里斯检测器的一些特性
- 对于旋转不变
- 图像强度:加法乘法不改变
加法:导数不变
乘法:导数整体变化 - 缩放,会改变
尺度不变性的检测
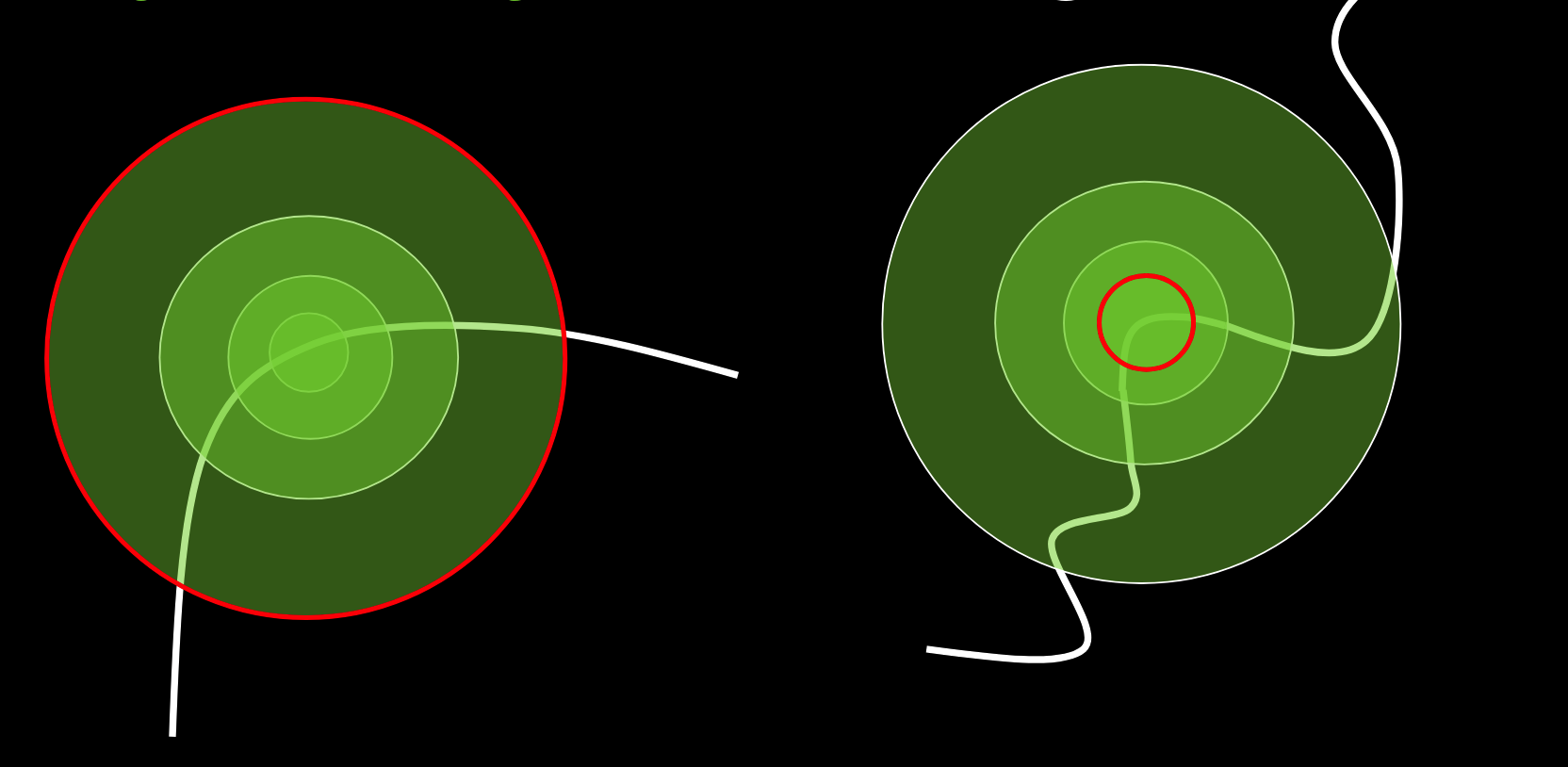
增大窗口,保持尺度不变
领域大小对函数的影响: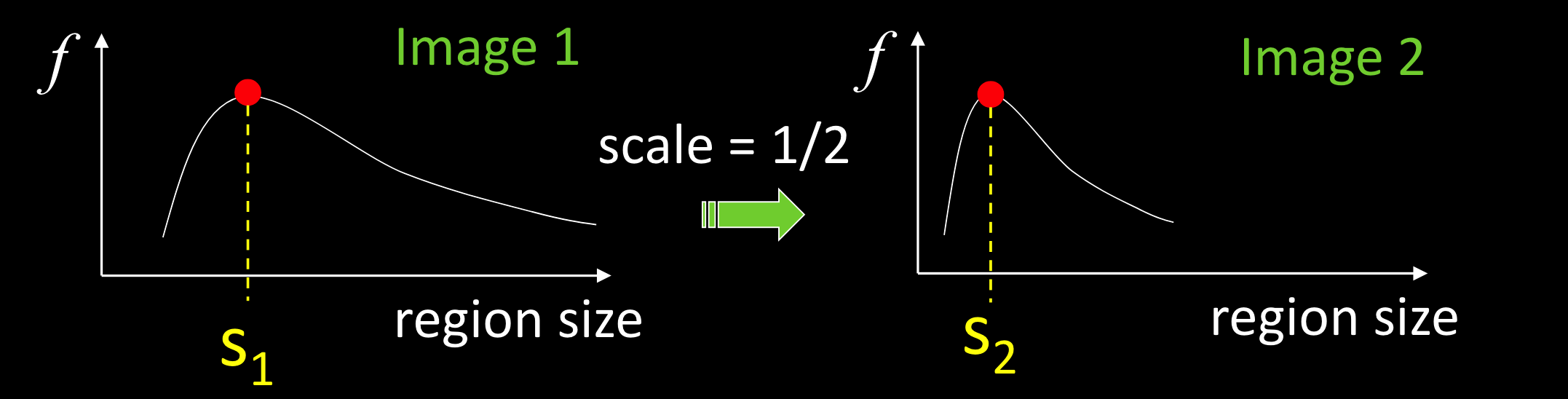
$S_1$, $S_2$,具有相同的缩放比例
一个好的尺寸检测函数

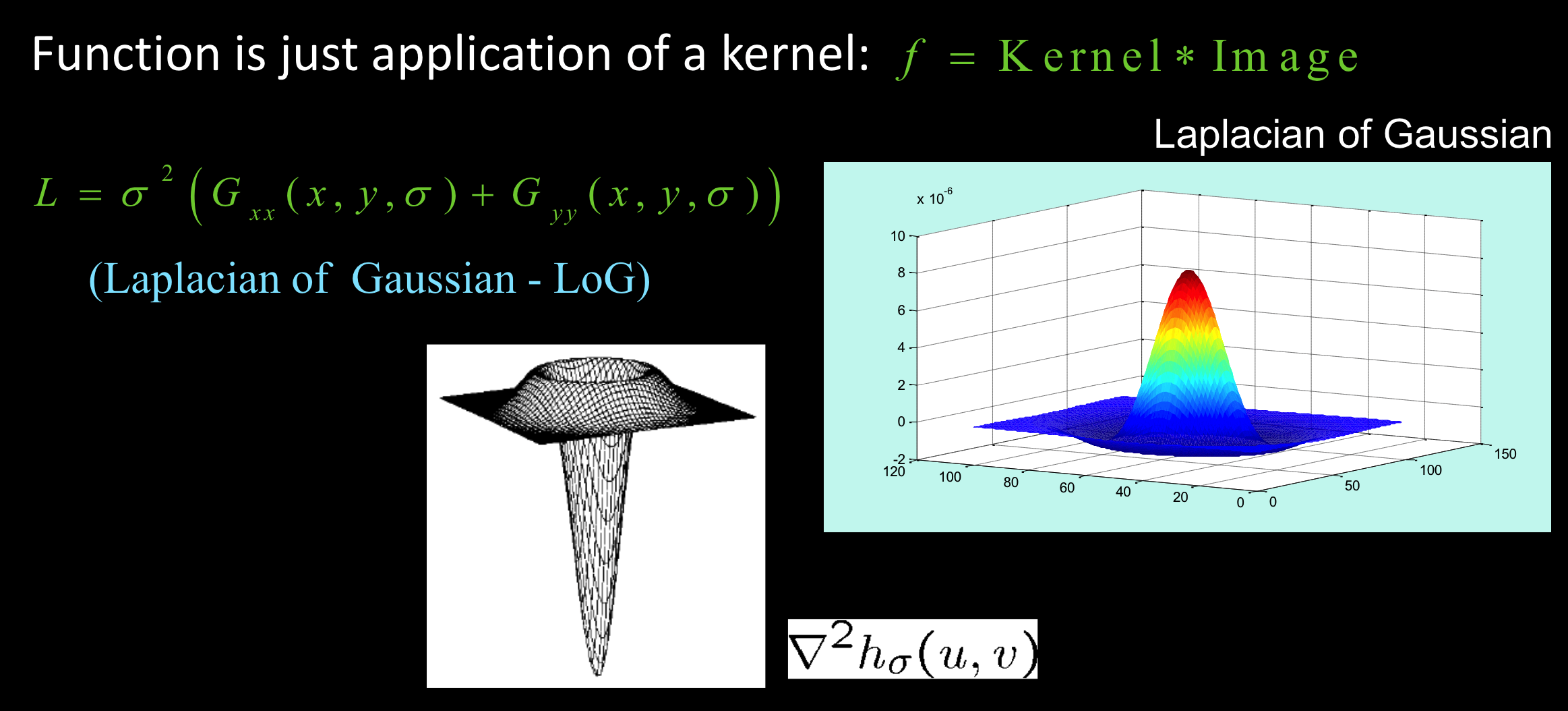
拉普拉斯差和高斯差几乎相同,选择高斯简化计算。
关键点定位
SIFT: Scale Invariant Feature Transform
尺度不变特征变换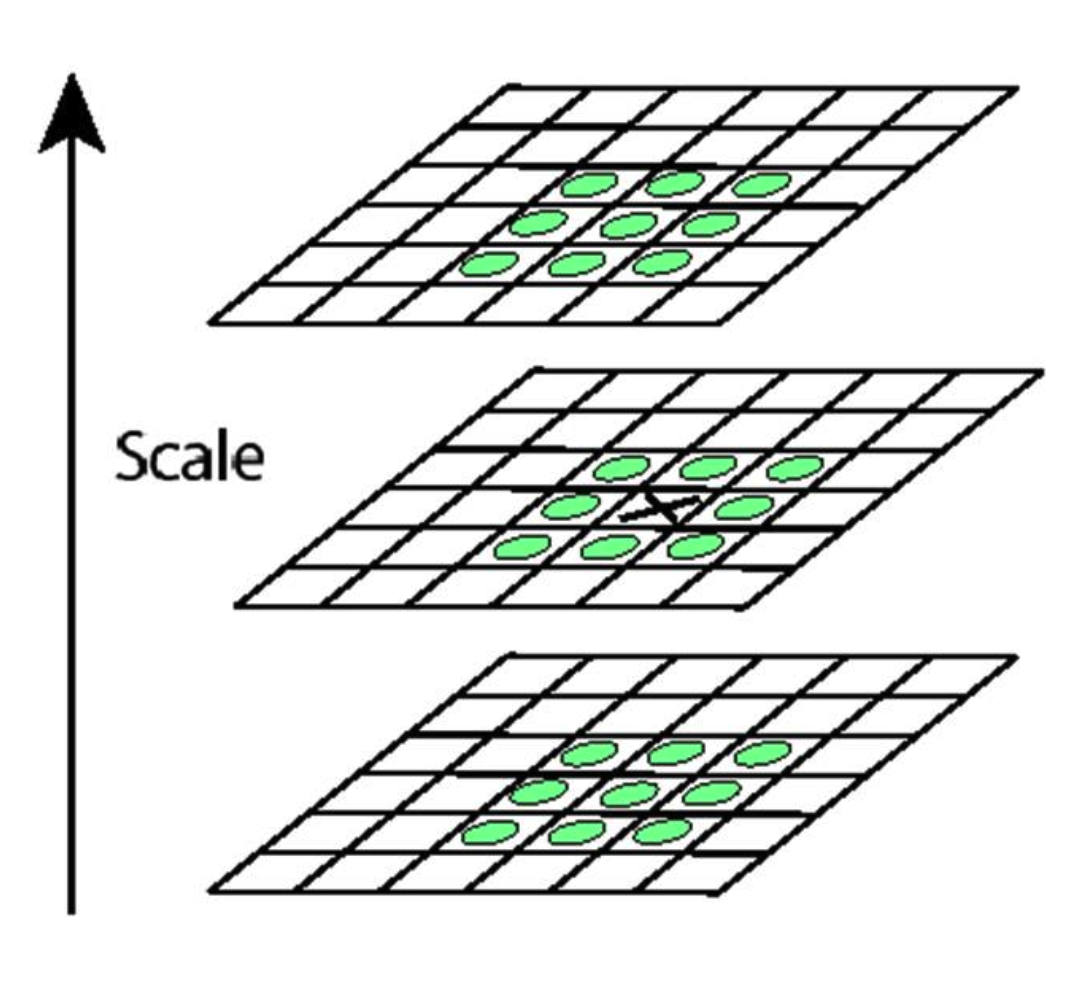
取不同尺寸的图像,不断模糊图像,两两相减,计算他们的高斯图像差异。
像素与周围九个像素比较,以及不同比例邻居上的比较,的看是不是极值。
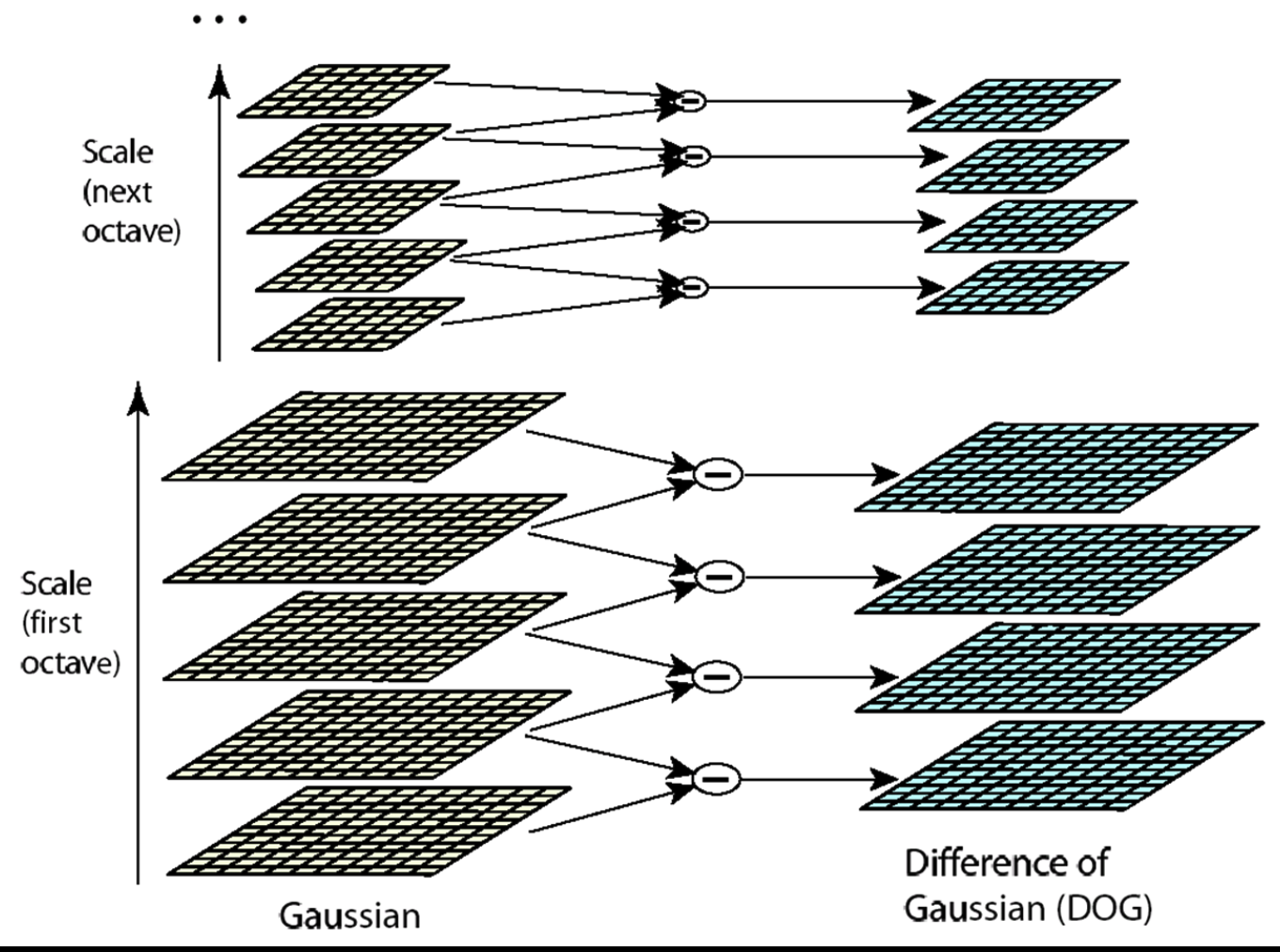
例子:
哈里斯-拉普拉斯算法:
先试用哈里斯角点检测
然后在看尺度方向上的拉普拉斯算子,找空间极值
特征描述
描述符:对领域进行描述
- 独特:不同的点有不同的描述符
- 可区分
- 几乎相同
SIFT: Scale Invariant Feature Detection
尺度不变特征变换
思想:
- 图像内容是一组特征:对于平移,旋转,放缩等图像处理操作是不变的
- 描述符是稳健的
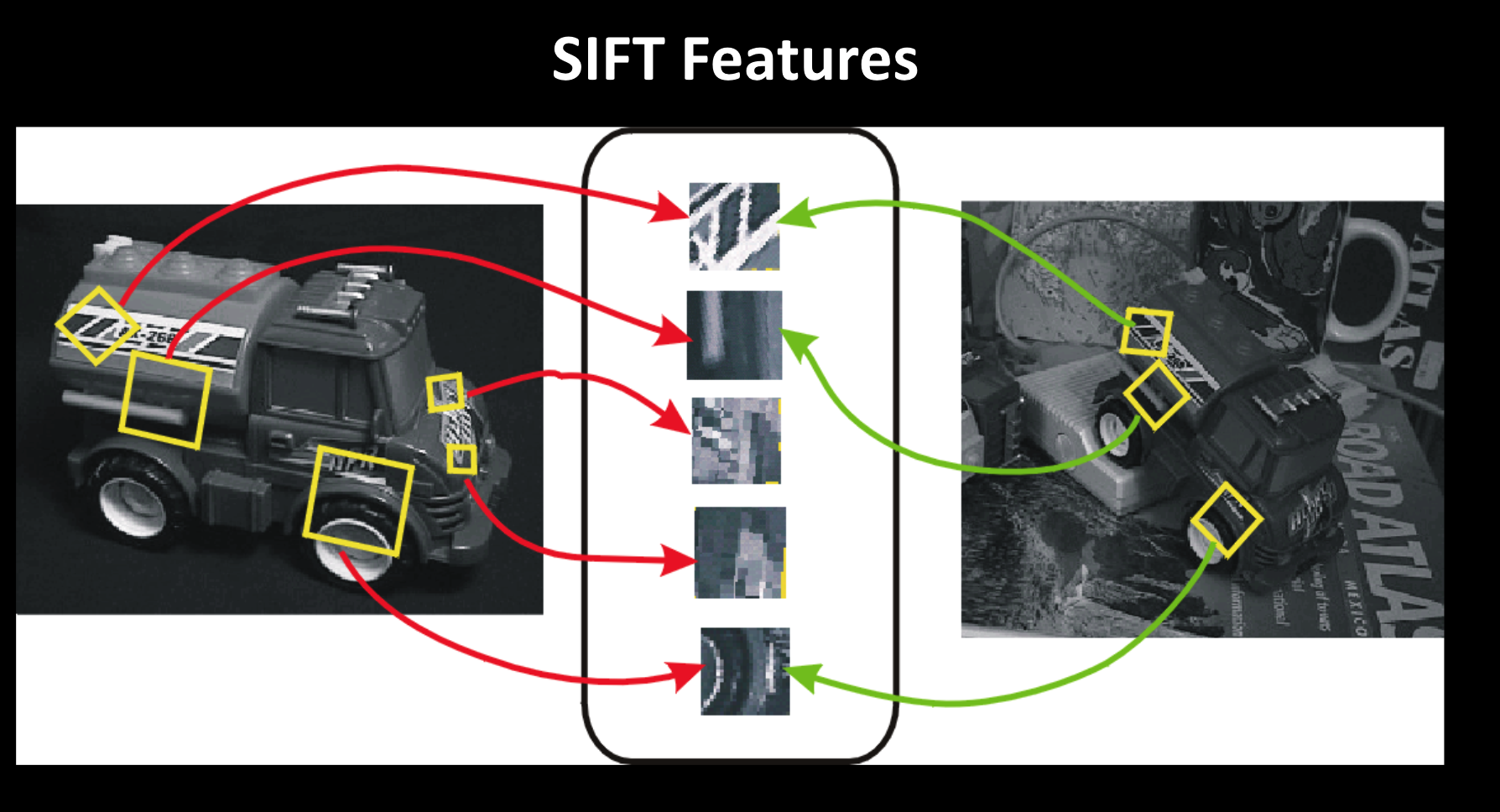
总体SIFT识别过程
- 确定关键点尺寸
- 定位关键点
- 找到领域的局部的方向
- 关键点描述

右图中的方向箭头,就是局部方向。
计算局部方向
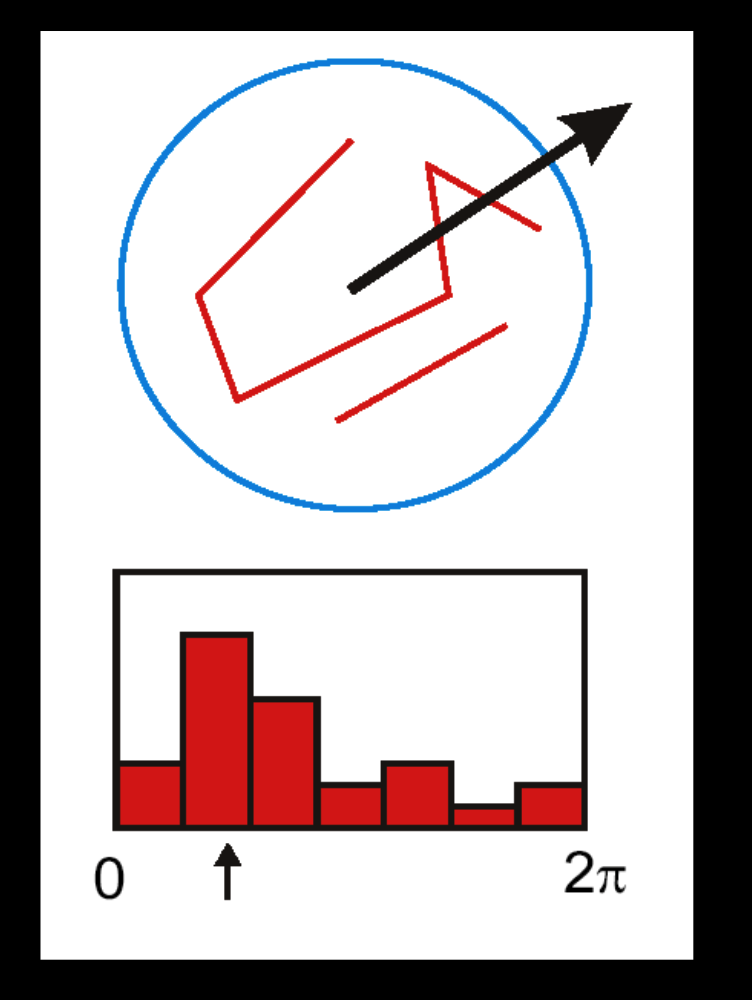
图中是方向直方图
找到一个峰值,就是主导方向,我们需要使用的方向,以这个方向为北方。
关键点描述符
标准化:
旋转到新的北方朝上
放缩到相同尺寸
SIFT特征向量: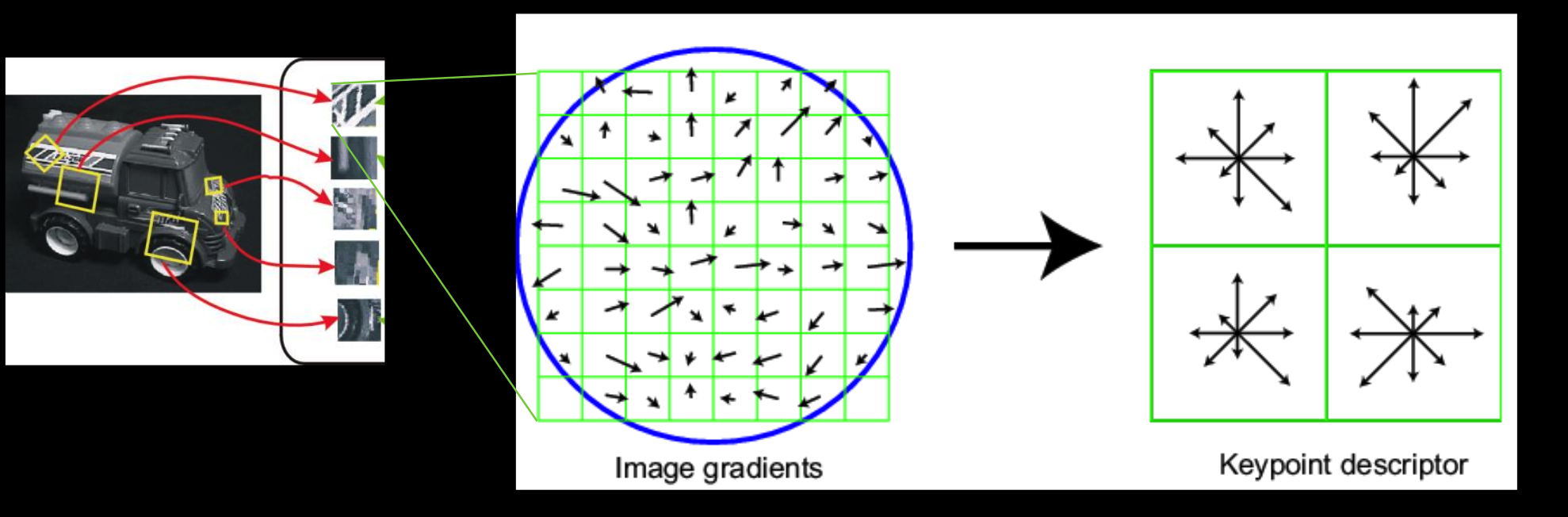
右图是一个:2X2的图,最好是使用4X4的直方图,一个里面有8个方向,叠加到一起,一个特征会有128个向量
将所有的向量,标准化到内积为1。
梯度:直方图加权梯度,方向最大的权最高
评估SIFT描述符:
通常一个直方图有8个方向,采用4X4的直方图,向量长128。
匹配特征点
如何在两个图的特征中,找到匹配的特征点?
最邻近算法匹配
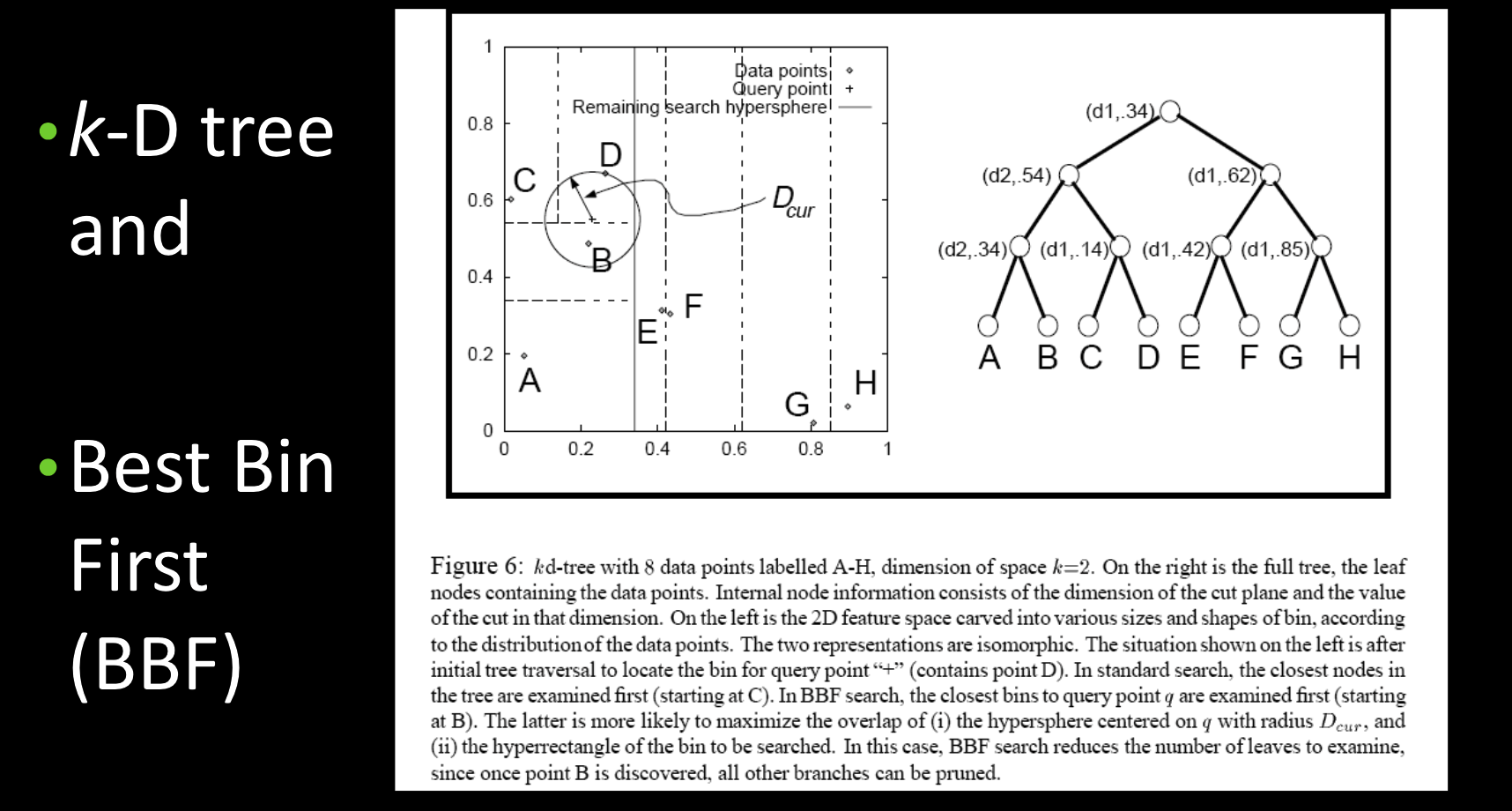
best-bin-first 算法基于k-d树
基于小波的散列

小波:是一种接近滤波器的形式,从三个滤波器里输出三个数。
思想类似局部敏感哈希: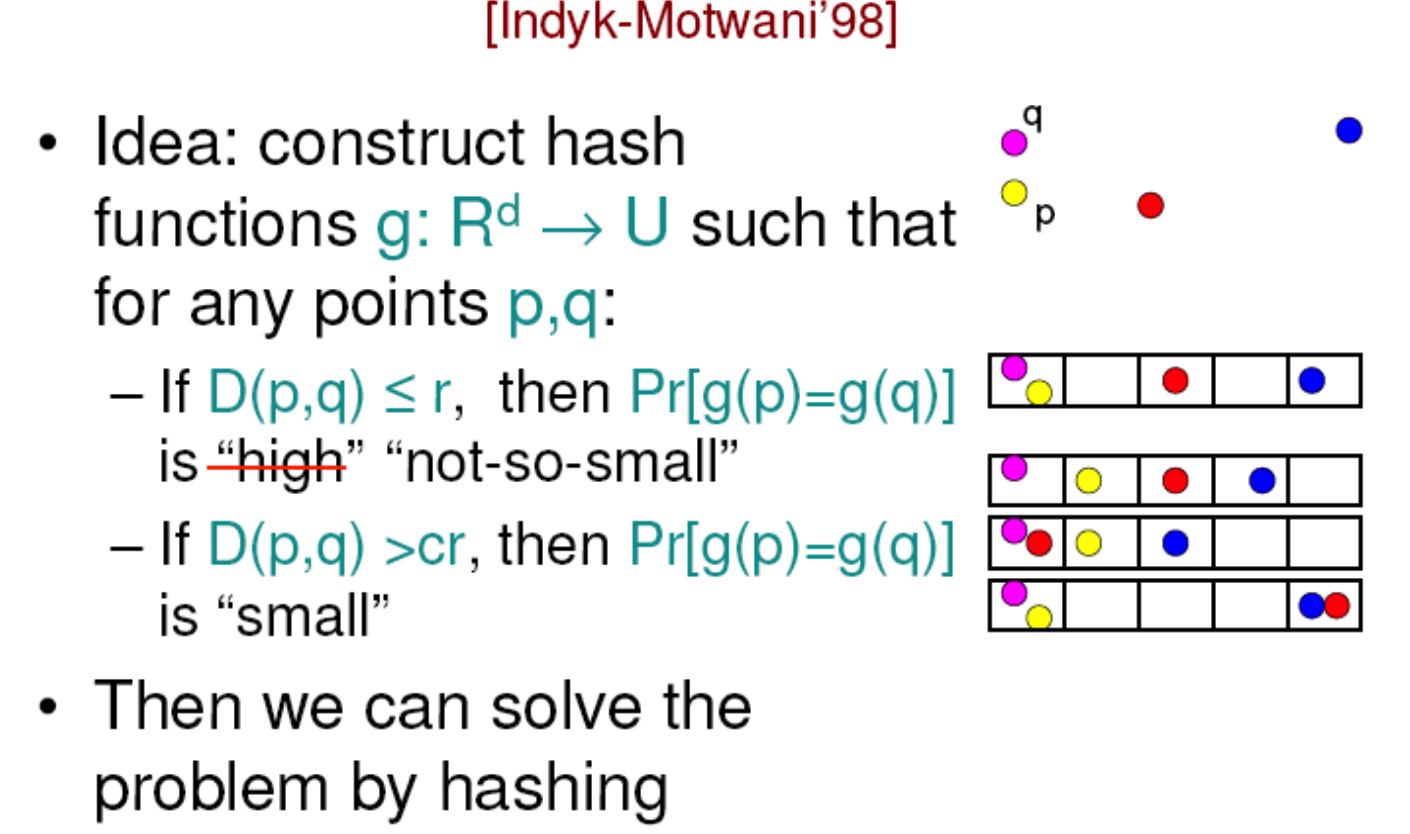
考虑了空间两点的距离
例子 3D物体识别

从测试图中匹配:
例子 遮挡下的识别
通过部分关键点,预测其他点去哪里了。
鲁棒误差函数
SSD:差的平方和
NN: 最近邻居
Lowe a better way
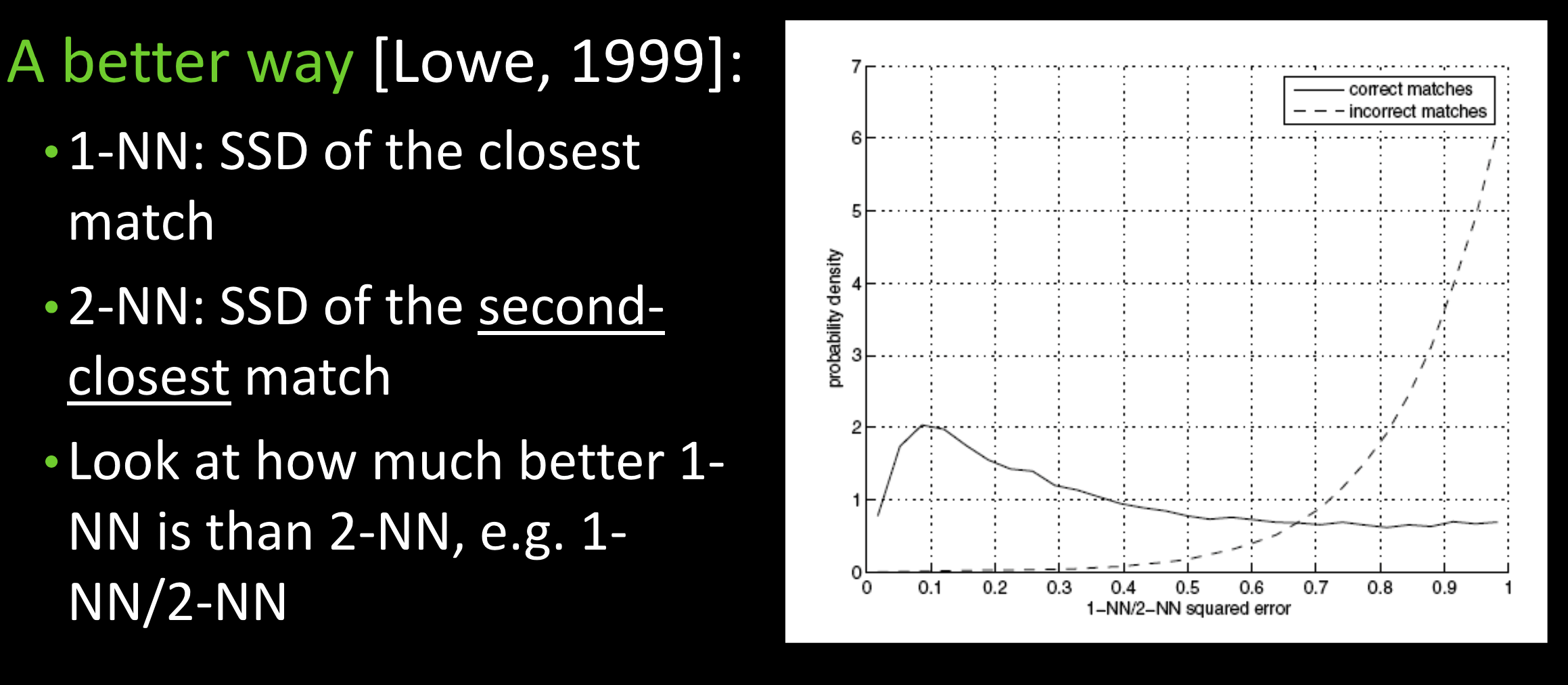
意义:
如果最佳匹配被遮挡了,第一和第二匹配相差不大,说明没有找到正确的匹配。
模型拟合
最小二乘线拟合 Typical least squares line fitting
机器学习内容
只是$y$方向上的拟合。
总体最小二乘法
$ax+by=d$
$E=\sum_{i=1}^n(ax_i+by_i-d)^2$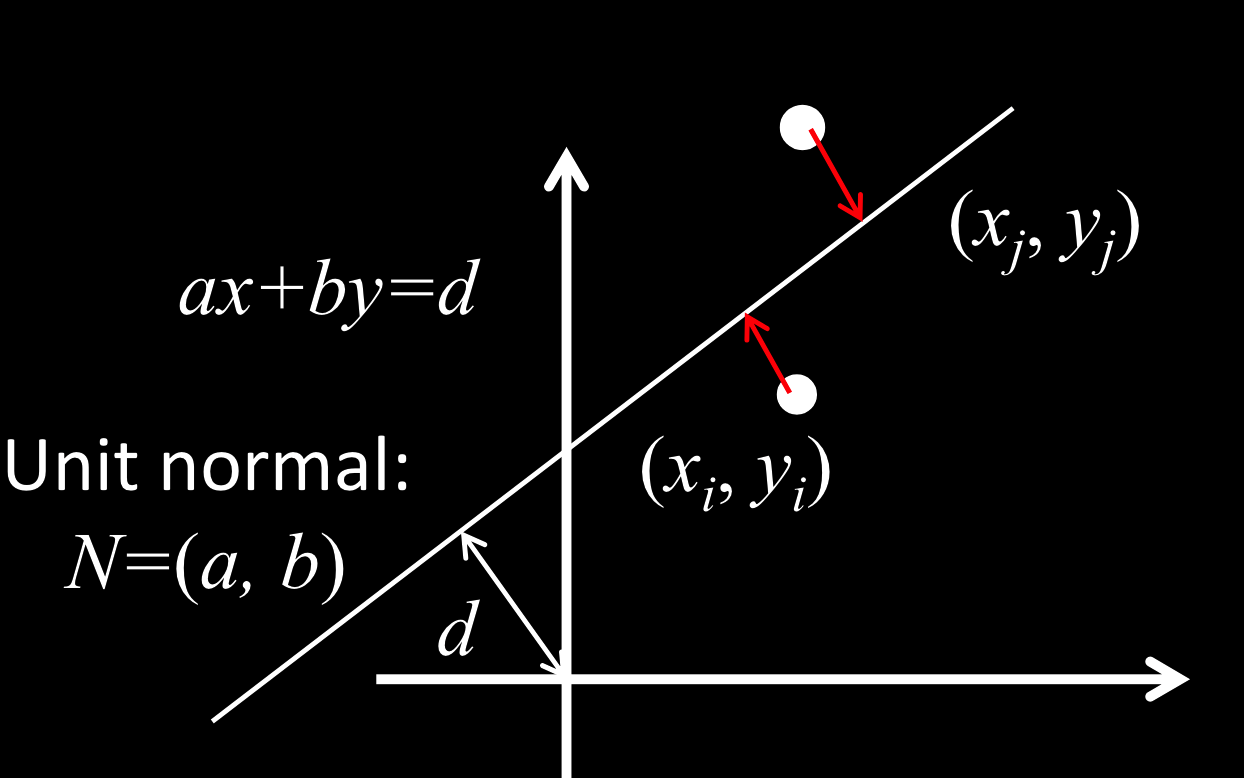
推导公式:
\begin{split}
\frac{\partial E}{\partial d}=\sum_{i=1}^n-2\left(ax_i+by_i-d\right)=0\\
\Rightarrow d=\frac an\sum_{i=1}^nx_i+\frac bn\sum_{i=1}^nx_i=a\overline{x}+b\overline{y}
\end{split}
\begin{split}
&E = \sum_{i=1}^{n}(a (x_{i}-\overline{x})+b (y_{i}-
\overline{y}))^{2}\\
&=\left\|\begin{bmatrix}x_{i}-\overline{x}&y_{i}-
\overline{y}\\
\vdots&\vdots&\vdots\\
\lfloor x_{i}-\overline{x}&y_{i}-\overline{y}\rfloor
\end{bmatrix}\begin{bmatrix}a\\
b\end{bmatrix}\right\|^{2} \\
&=\left(U \mathbf{h}\right)^{T}\left(U \mathbf{h}\right)\\
&\frac{dE}{d\mathbf{h}}=2(U^TU)\mathbf{h}=0
\end{split}

- 实际测量点$(x,y)$ 等于真实点$(u,v)$垂直于$a,b$方向上的偏动。
- 符合高斯噪声
鲁棒估计器
求一个最小化:$\sum_i\rho\left(r_i\left(x_i,\theta_1\right);
\sigma_1\right)$
- $r_i\left(x_i,\theta_1\right)$:代表残差值,该点距离拟合曲线的距离
- $\rho$:有尺度参数$\sigma$鲁棒函数
一种鲁棒函数: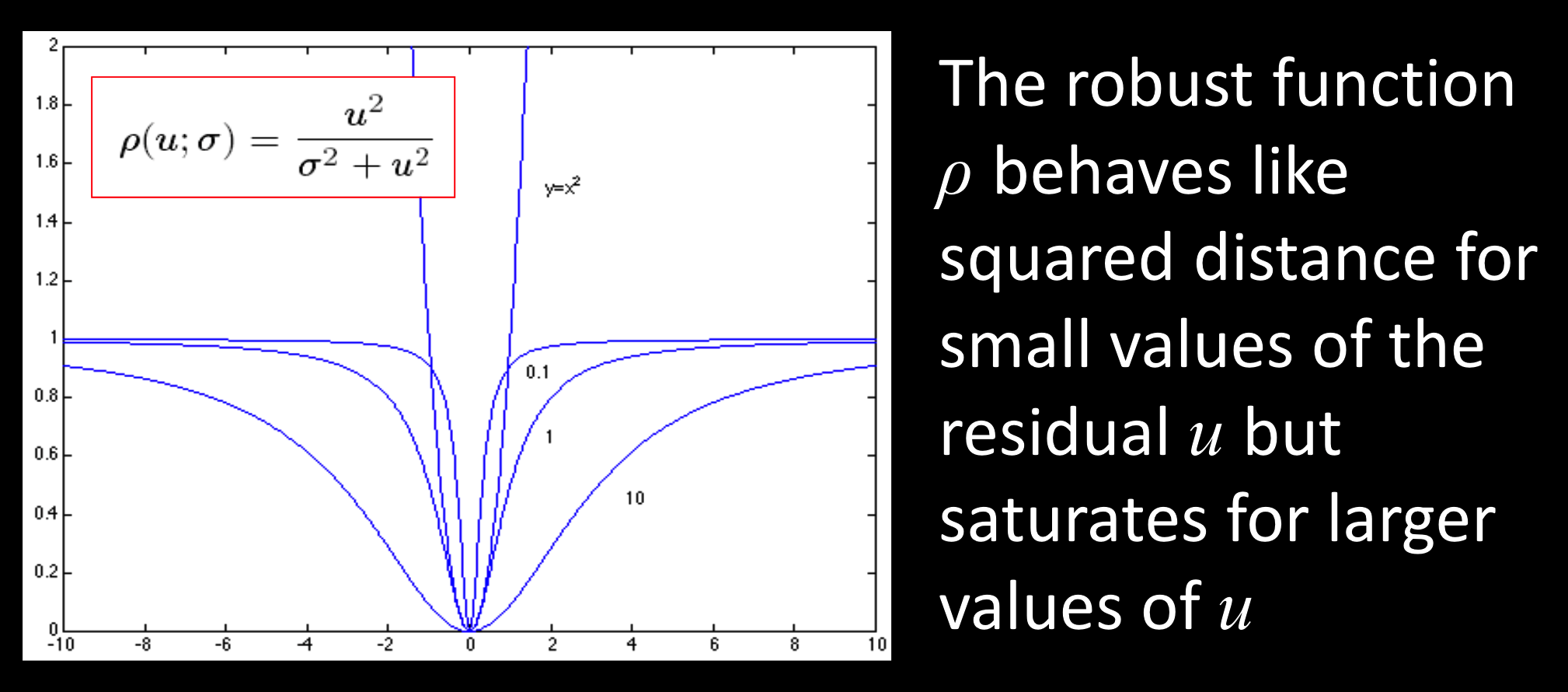
- 当$u$很小的时候:
- 当$u$很大的时候:误差很大
RANSAC算法 RANdom SAmple Consensus
一般模型
选取模型的最小集点数量:
距离阀值:
$f(d)=\frac{\sqrt{2}e^{-(\frac{d^2}{2\sigma^2})} }
{\sqrt{\pi}\sigma},d\geq0$
计算N

模型所需的样本点数:
$N > \log(1 - p ) / \log(1 - (1 - e )^S )$
例子
两个匹配的特征: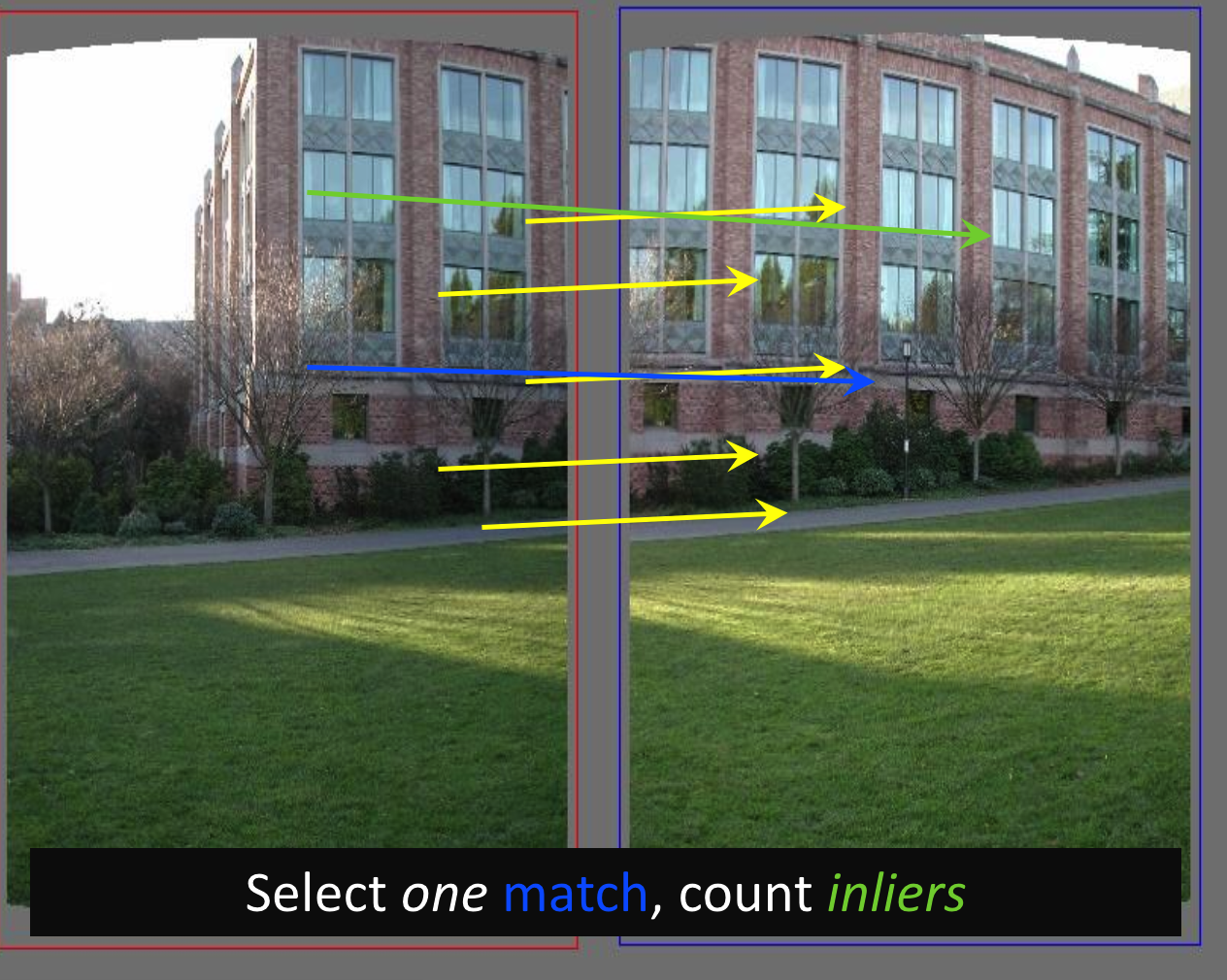
- 有5个特征匹配,2个不匹配,认为这两张图是相同的,错误
- 因为匹配特征中有噪音
RANSAC算法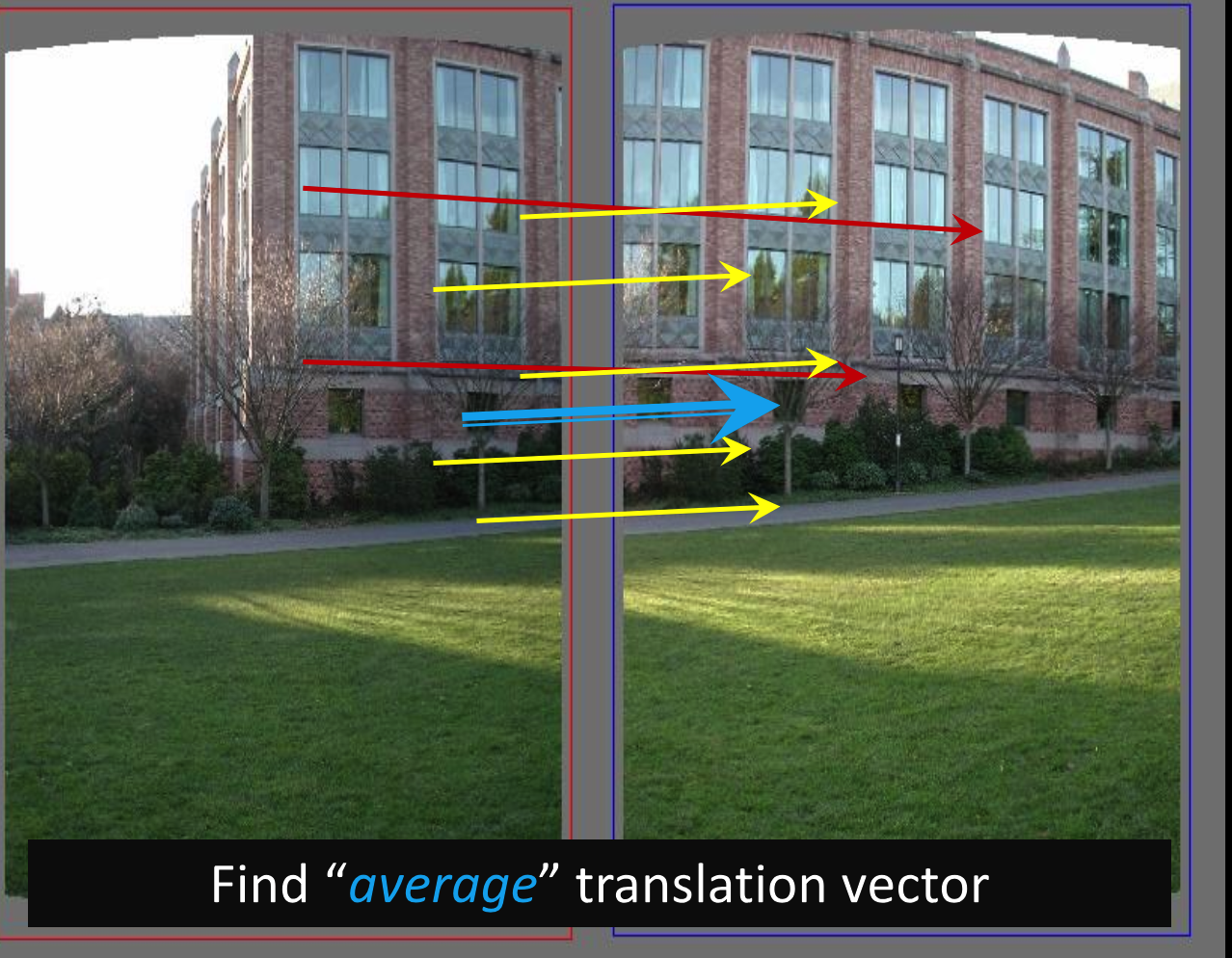
- 去除高斯噪音,选择平均值
RANSAC算法 循环
