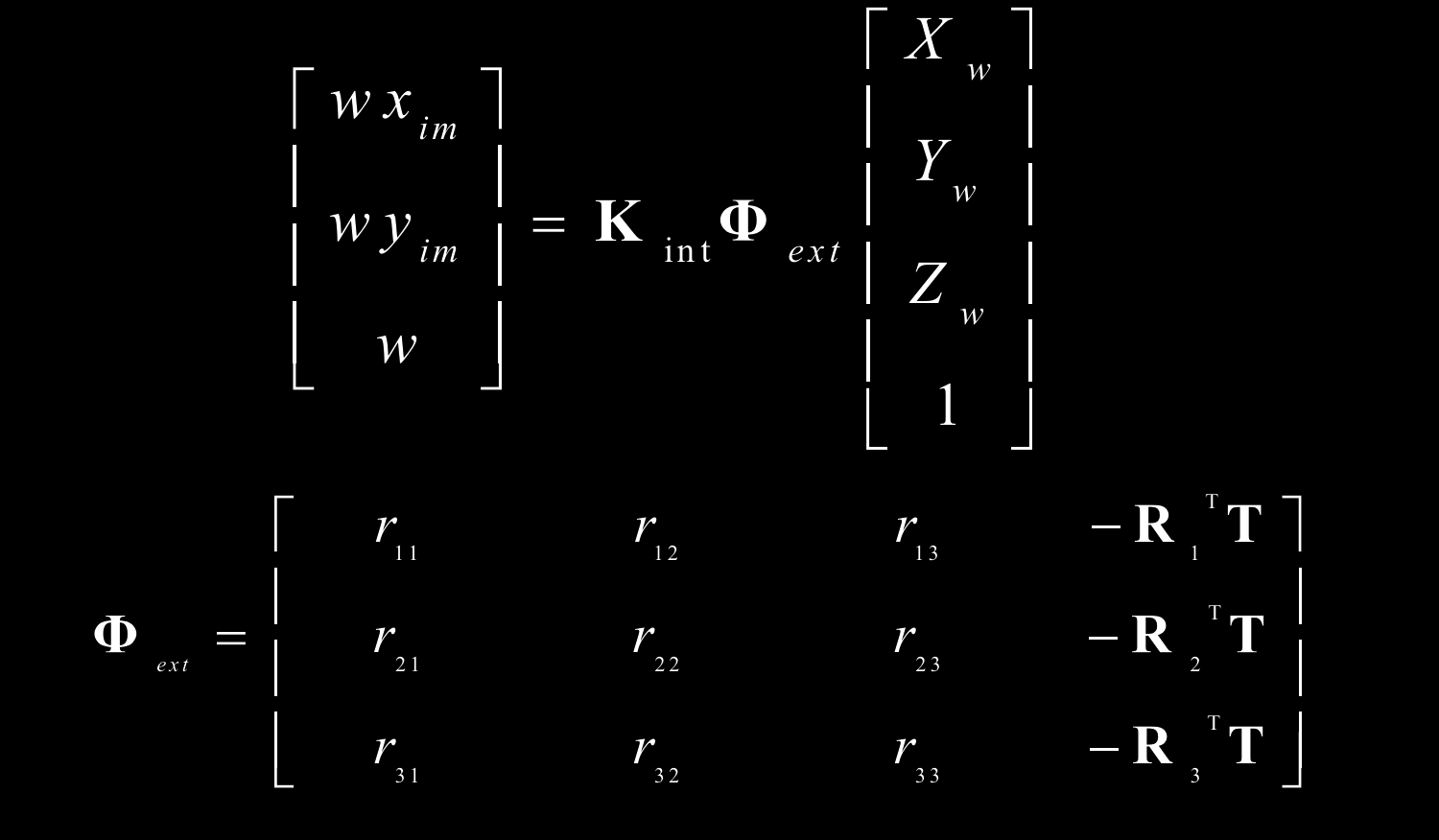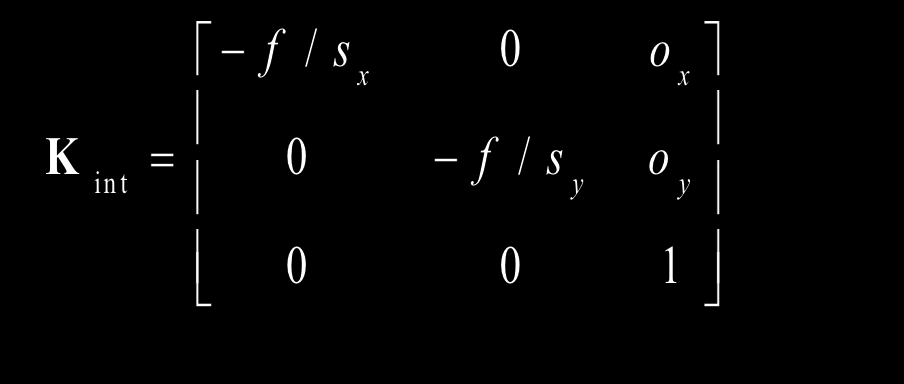计算机视觉概论 相机和图像
更新历史
- 24.04.29:初稿
系列
透视成像
建模投影
坐标系:
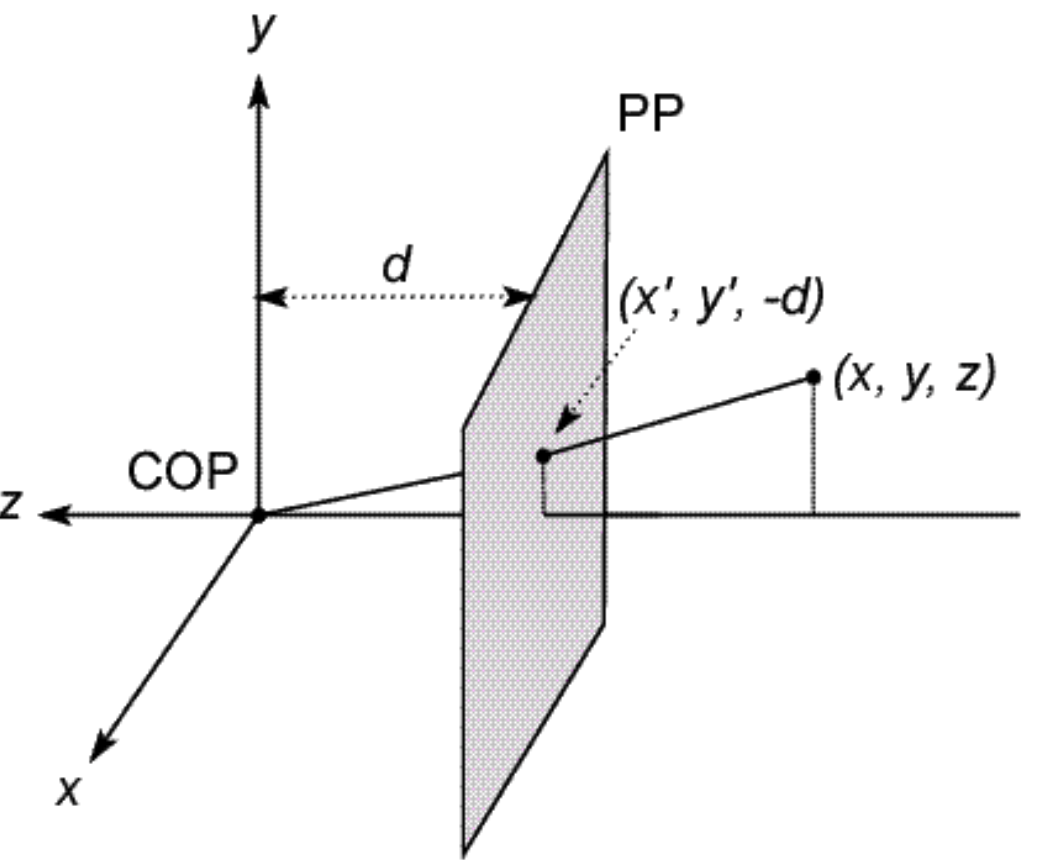
- Center OF Projection:光学中心,在原点
- 不用担心翻转,图像放在坐标系前
- 坐标系符合右手定则,$z$轴指向相机,而不是指向世界
坐标转换:
$(X,Y,Z)\to(-d\frac XZ,-d\frac YZ,-d)$
齐次坐标 Homogeneous coordinates
二维:
$(x,y)\Rightarrow\left[\begin{array}{c}x\\y\\\mathbf{1}\end{array}\right]$
三维:
$(x,y,z)\Rightarrow\left[\begin{array}{c}x\\y\\z\\\mathbf{1}\end{array}\right]$
齐次转常规:
$\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]\Rightarrow\left(x/w,y/w,z/w\right)$
例子:
\begin{split}
\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1/f&0\end{bmatrix}\begin{bmatrix}x\\|&|\\y\\z\\1\end{bmatrix}&=\begin{bmatrix}x\\y\\z/f\end{bmatrix}&\Rightarrow\left(f\frac xz,f\frac yz\right)\\&\Rightarrow\left(u,\nu\right)
\end{split}
通过焦距为$f$的投影,投影到世界上某个点$(x,y,z)$的图像中的坐标。
焦距:从中心投影到图像的距离
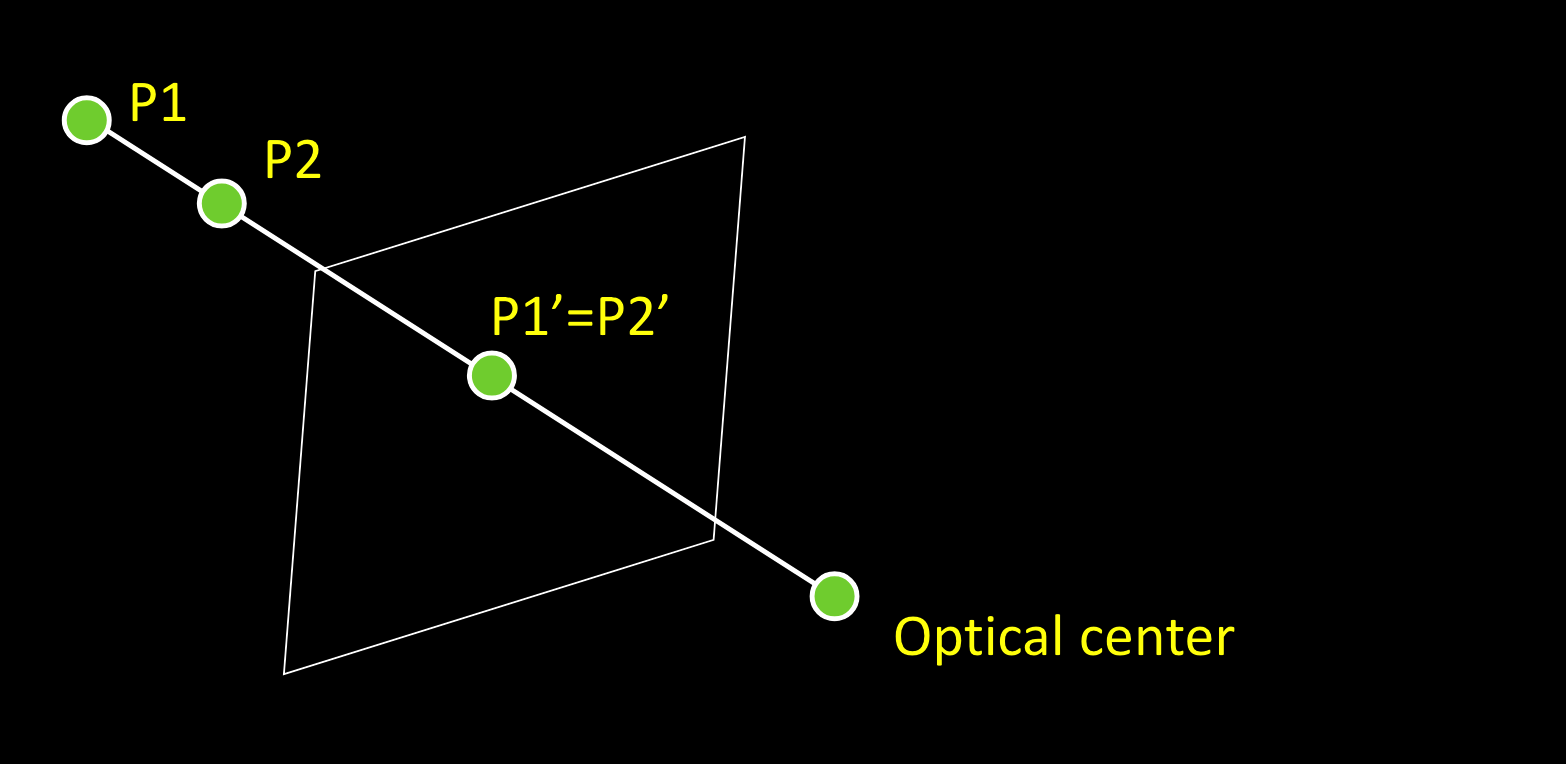
投影的几何性质
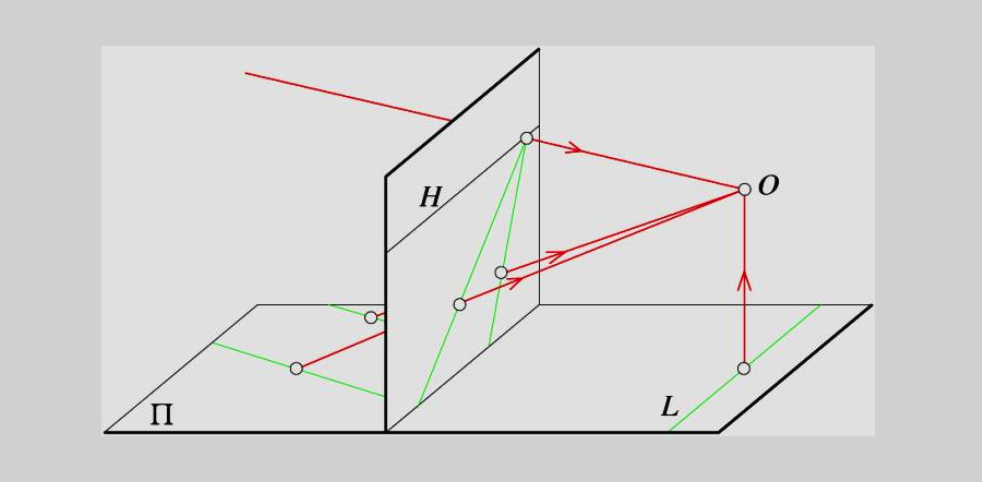
- $O$,是投影中心
- 点,线,投影到点,线
- 多边形投影会改变
平行线会改变:
数学解释:
三维平行线:
$x\left(t\right)=x_0+at\\y\left(t\right)=y_0+bt\\z\left(t\right)=z_0+ct$
投影坐标的投影方程:
$x’(t)=\frac{fx}z=\frac{f\left(x_0+at\right)}{z_0+ct}\\y’(t)=\frac{fy}z=\frac{f\left(y_0+bt\right)}{z_0+ct}$
$\begin{split}&\text{In the limit as }t\to\pm\infty\quad x’(t)\to\frac{fa}c,\quad y’(t)\to\frac{fb}c\\&\text{we have (for }c\neq0){:}\end{split}$
- 公式中没有$x_0,y_0,z_0$,直线的起点不重要,直线沿着直线一直向前
- 不同的直线会汇聚到同一个点,(点不一定相同,取决于视角)
- $c$不能为0,如果c为0,意味着平行线与$z$轴垂直,与投影面平行,永远不会相交
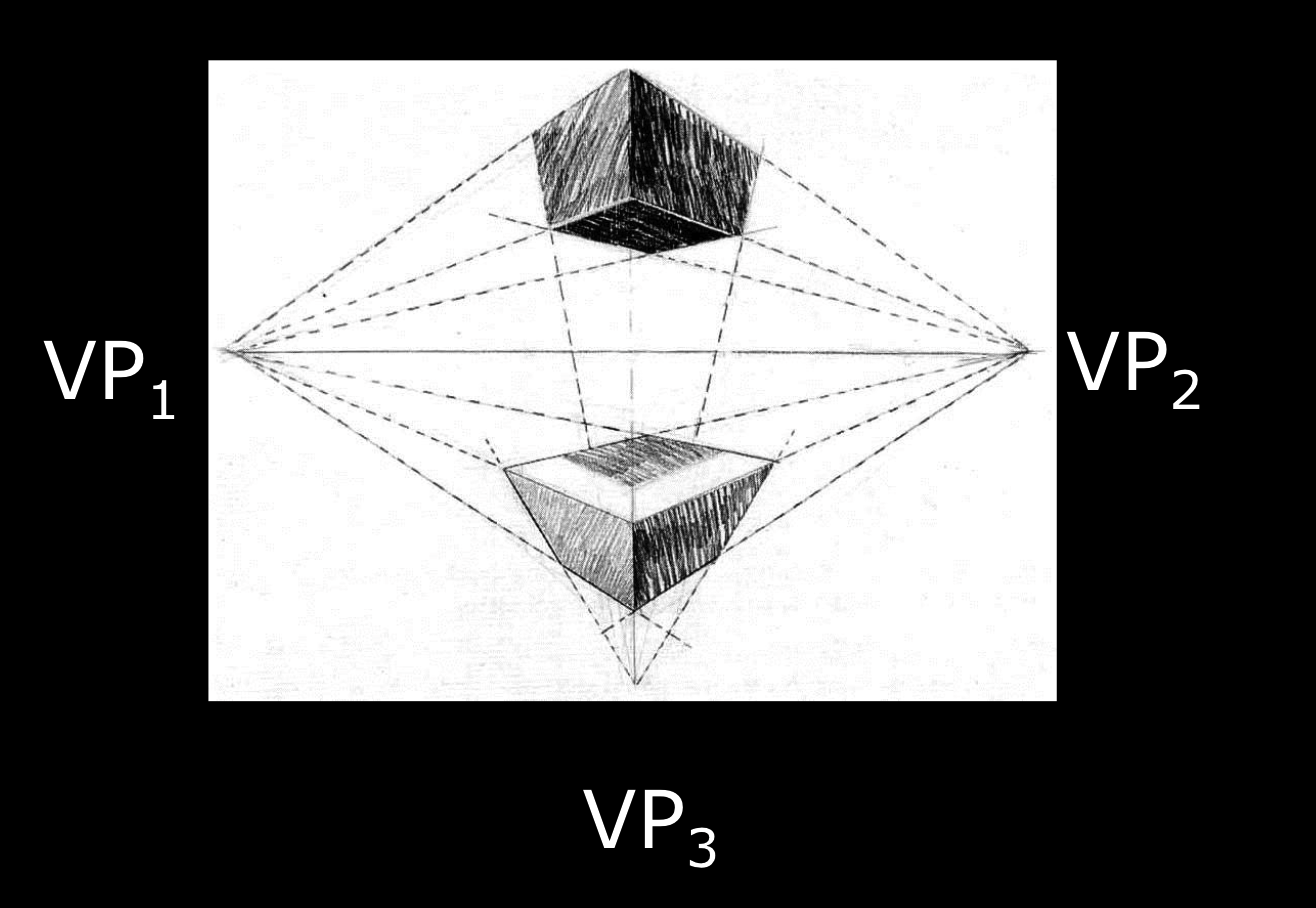
平行线会在无限远的地方汇聚消失:消失点
三点透视
人类视觉:Müller-LyerIllusion
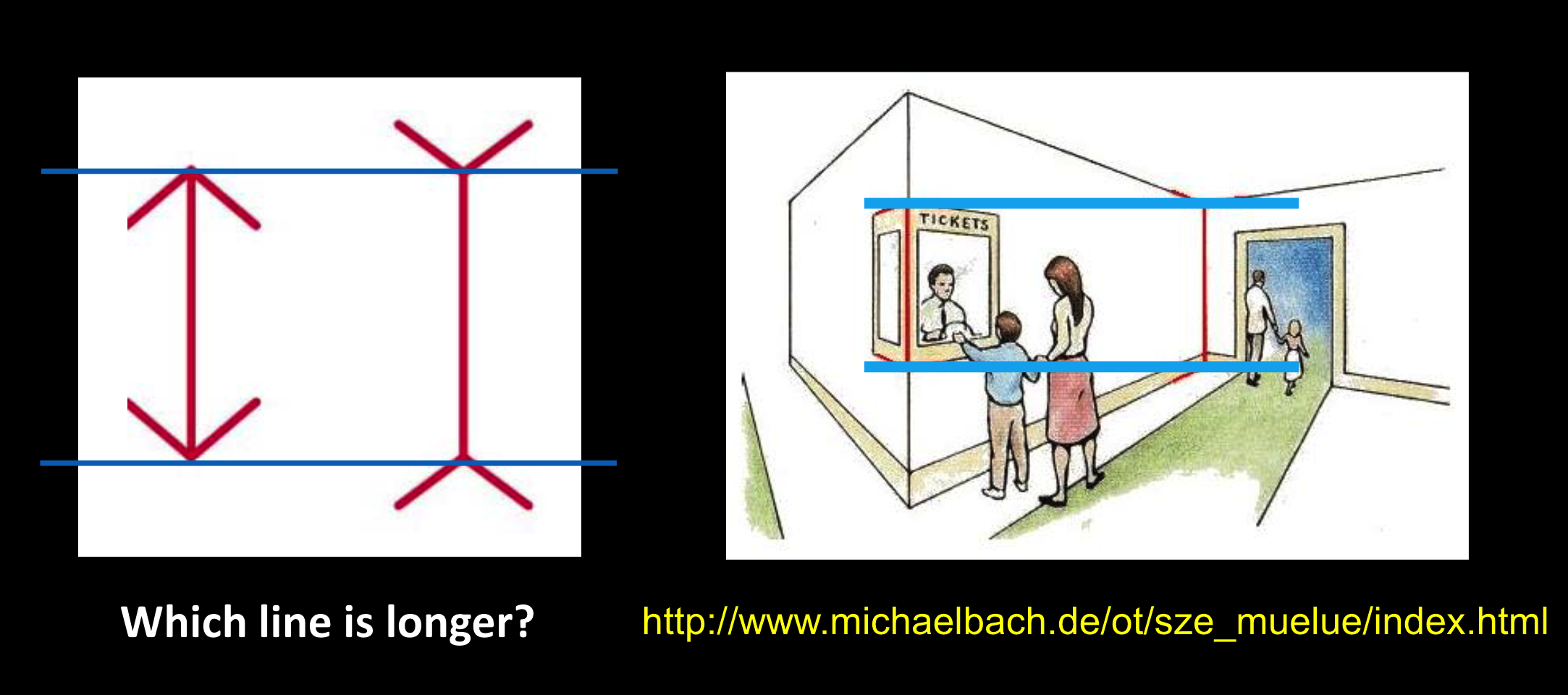
红线哪个更长,透视错觉
其他投影模型
正交投影: Orthographic
特殊的平行投影,假设光源无限远,光是平行的。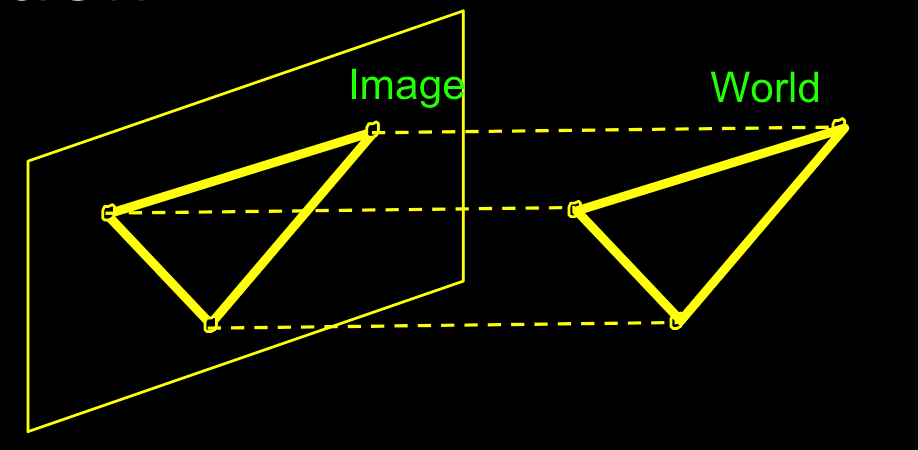
投影矩阵:
$\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&0&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\1\end{array}\right]\boldsymbol{=}\left[\begin{array}{c}x\\y\\1\end{array}\right]\boldsymbol{\Rightarrow}(x,y)$
弱视角投影: Weak perspective
缩放投影
$\begin{bmatrix}1&0&0&0\\0&1&0&0\\\\0&0&0&1/s\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}=\begin{bmatrix}x\\y\\1/s\end{bmatrix}\Rightarrow(sx,sy)$
- $s$:缩放因子
立体几何
多视角图像
结构和深度是模糊的,所以出现了多视角,本质来自投影
人类视觉具有感知深度的能力,主要元素:
- 阴影 shading
- 纹理 texture
- 焦点/深度焦点 focus/defocus
- 移动 motion
立体视觉
两个眼睛看的图像不同,从两个视觉中恢复立体
双视觉图像,中心元素,前后的元素都在像它移动
随机点立体图:
人类可以直接融合双视角图像

相机是由光学中心(optical center)定义的
- 校准,相机姿态
- 图像对应点
简单的立体系统
相机的俯视图:

计算深度的公式:
$\begin{split}\frac{B-x_l+x_r}{Z-f}&=\frac BZ\\\\Z = f \frac B{x_l - x_r}\end{split}$
视角差为0,深度为无穷,月亮为什么一直会跟着,因为深度无限远,视角没有变化。
视角差的例子:

找出两张图,哪个在左边,哪个在右边,从上面的烟囱可以看出,右边图在右方拍摄。
红点是一个图像相同位置的点,右图向左移动一直,那个点才能到左图中的窗口点,这就是视角差。
从视差到深度:
通过视差图像,亮的地方视差大,暗的地方视差小。
根据视差与深度的反比关系,我们可以得到深度。
从深度到视差:
因为$y没有变化,视差来源于$x$,所以$D(x,y)$也是x的变化。
$(x’,y’)=(x+D(x,y), y)$
对极几何
立体对应约束
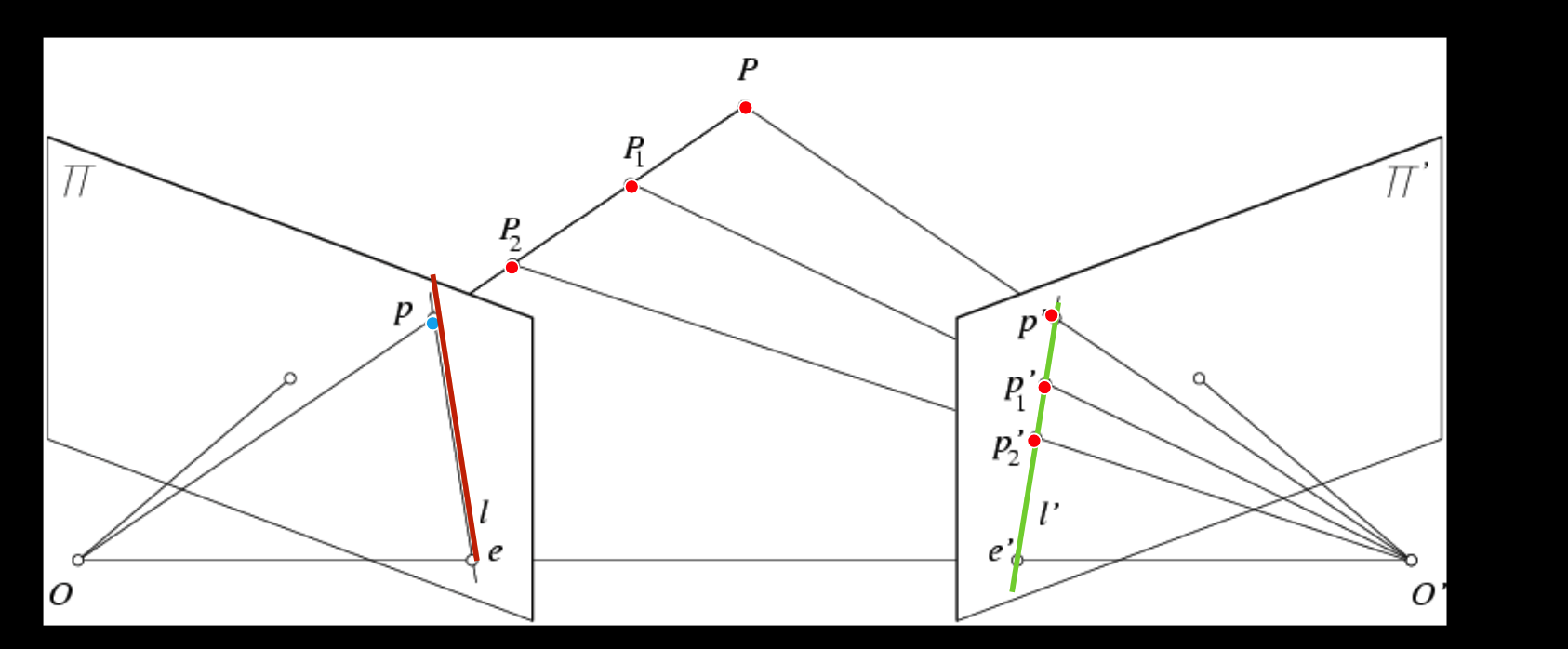
左侧的图像点p,可以点在一条直线上的任意一点,所以它对应在另一个图像中的点,是一条直线上任何一点。这条线成为极线。
这就叫做:极线约束 Epipolar constraint
- 基线:相机点和位置点形成的
为什么极线约束有用?
在极线中找对应另一个图像中的点。
例子:
极点是一个数学概念,所有的极线会在屏幕外面聚合。
平行图像的例子: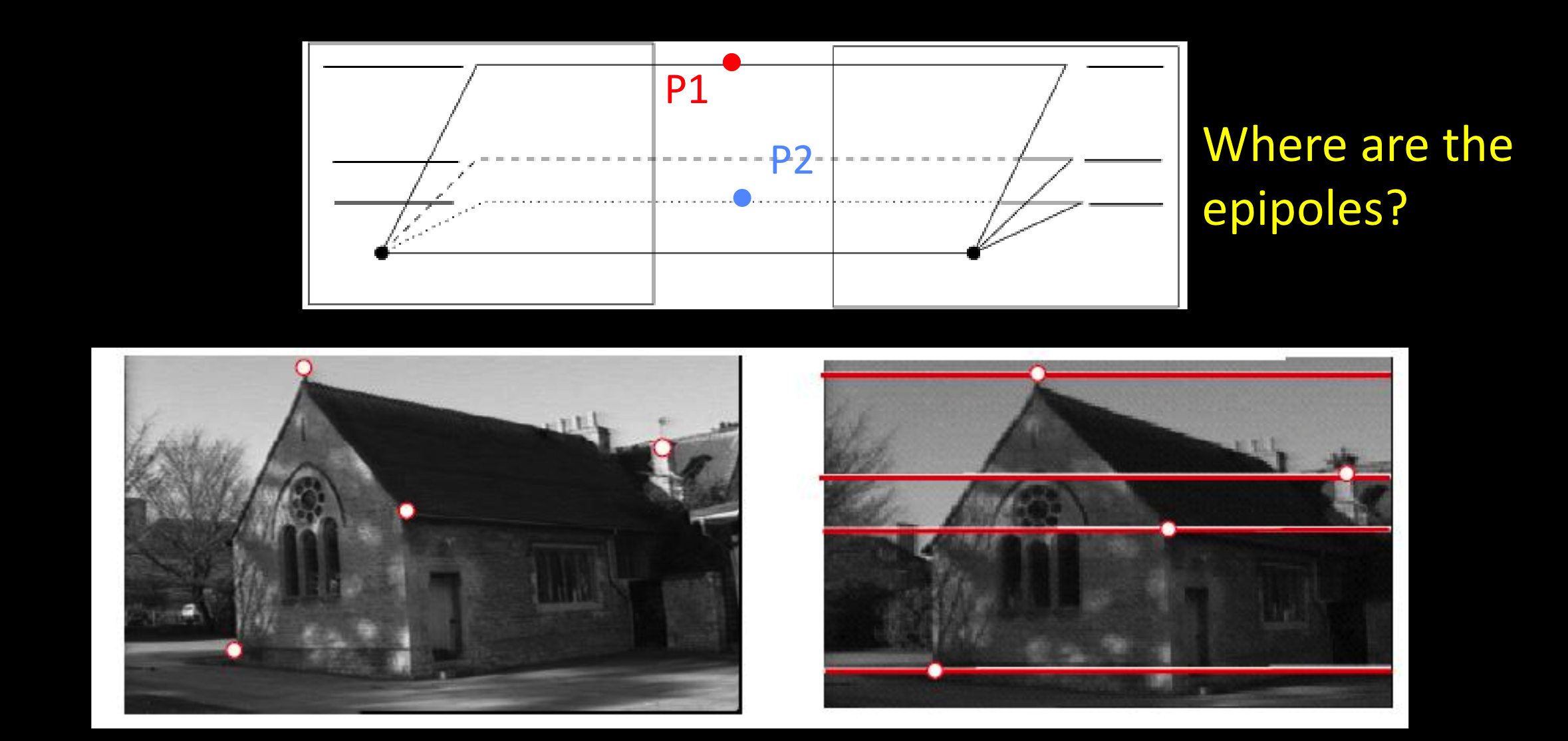
立体对应 Stereo correspondence
软约束:对应点之间的关系
- 相似性
- 唯一性
- 有序
- 视差梯度有限-深度变化不会太大
相似性
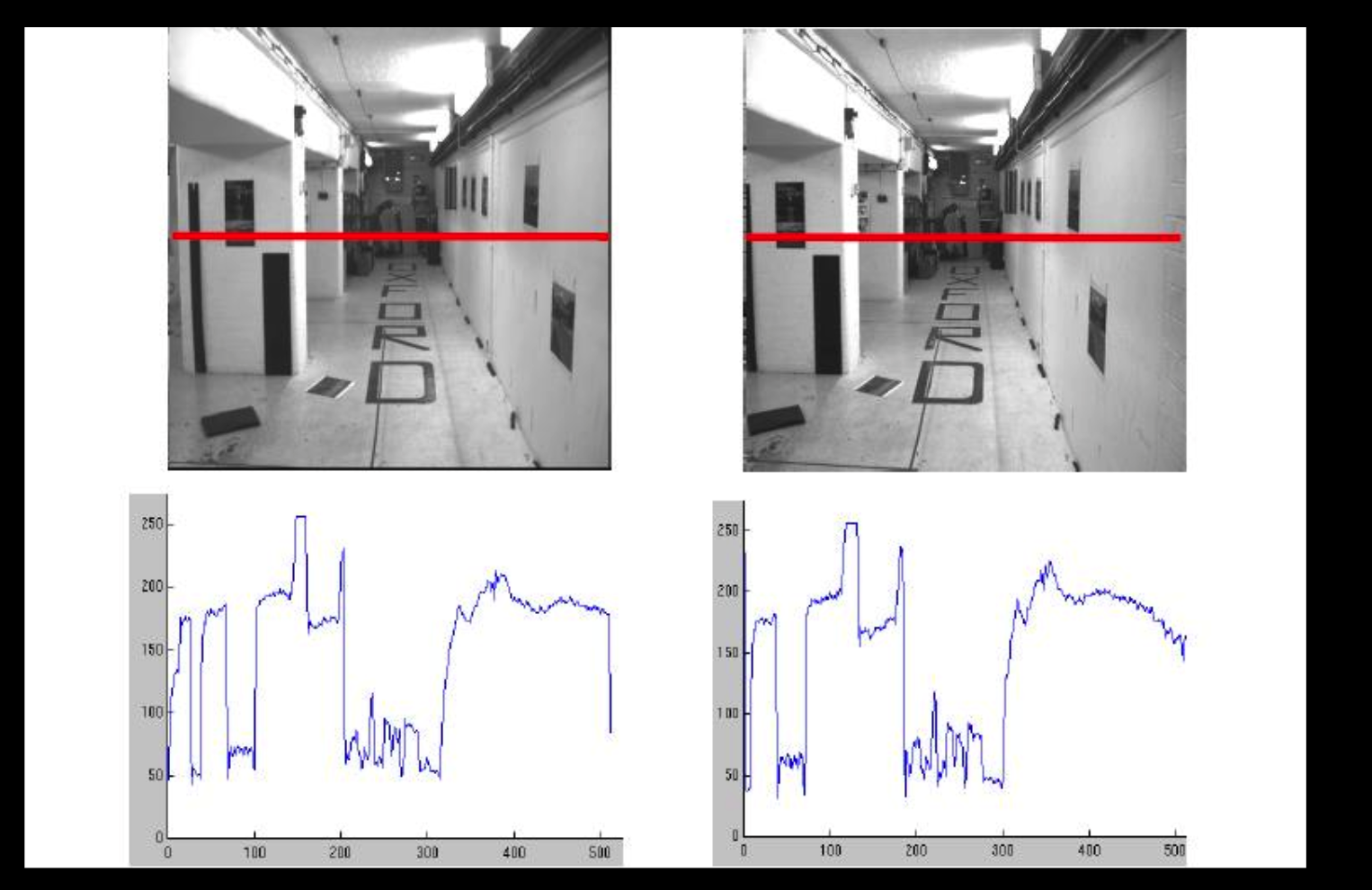
强度分布图:匹配位置具有差异
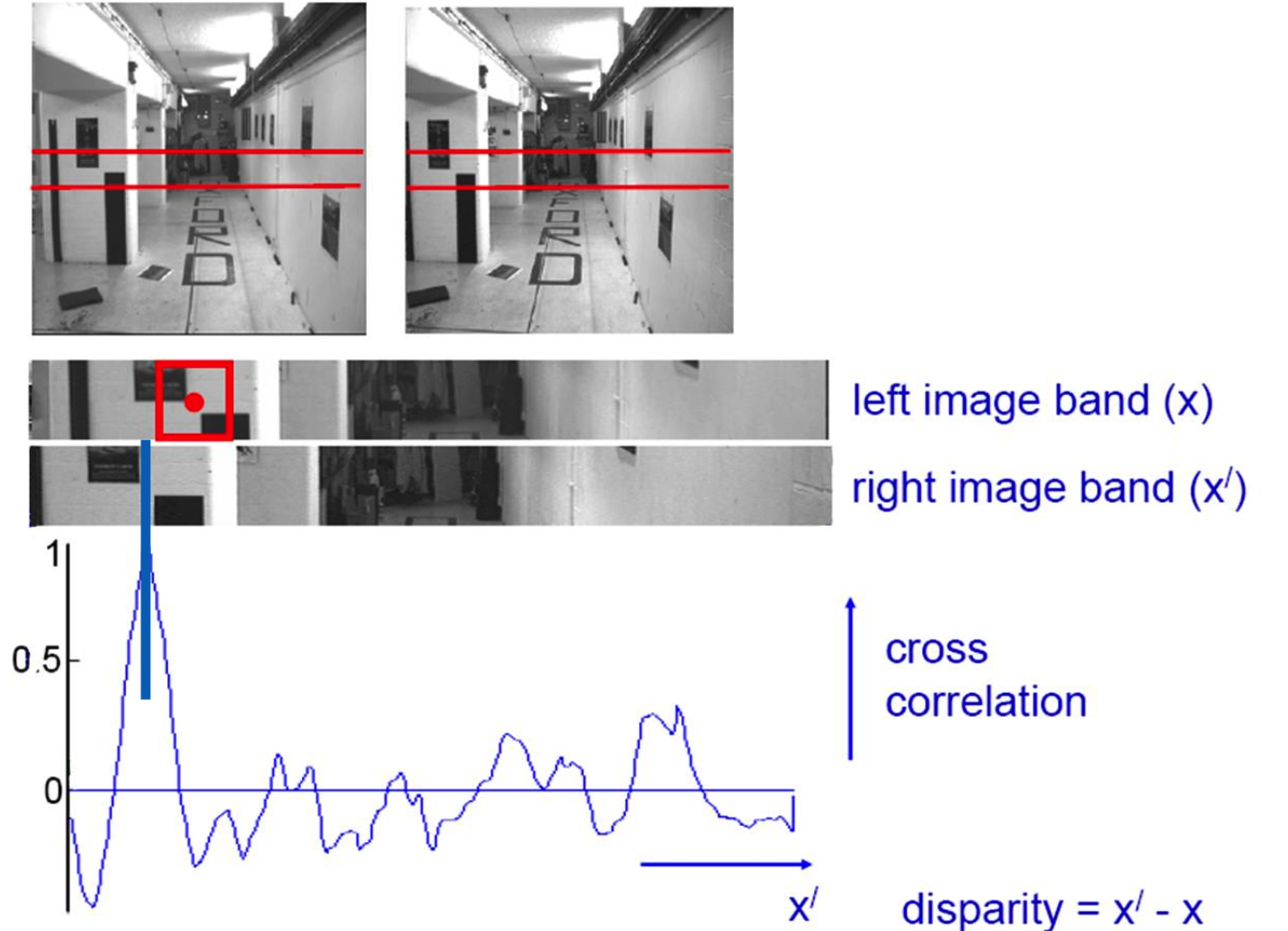
视差图的相似性:匹配的地方峰值最高
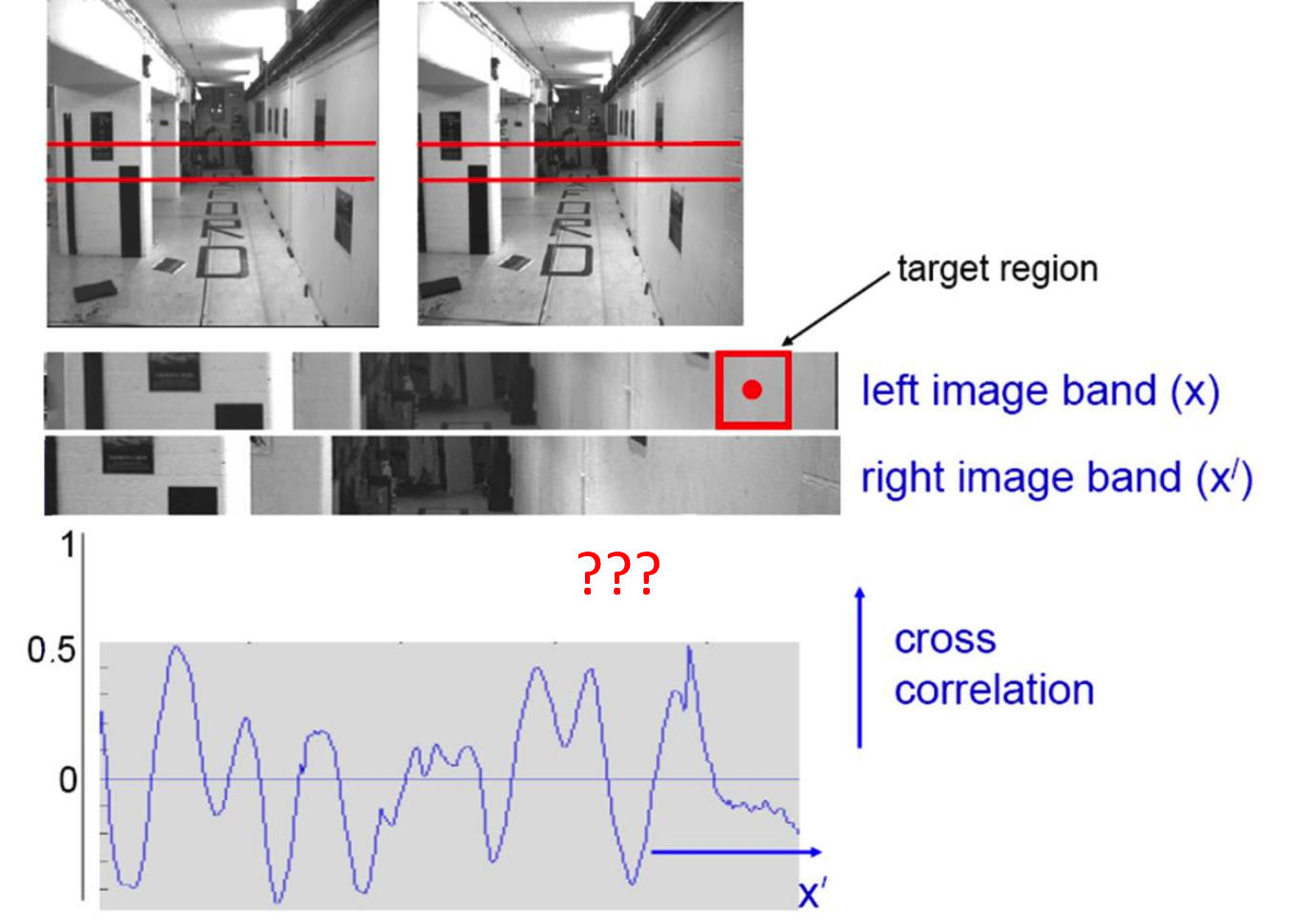
没有纹理的地方做匹配,没有匹配的地方?
原因:窗口太小,没有获得足够的纹理信息。
窗口大小的影响:
显示的是视差图
- 小窗口,获得了树干信息
- 大窗口,树干和背景融合到了一起
有序性
单一固体中:
左图中的点 $a,b,c$,在右图中有相同的顺序$a,b,c$。
例外:在一个透明的表面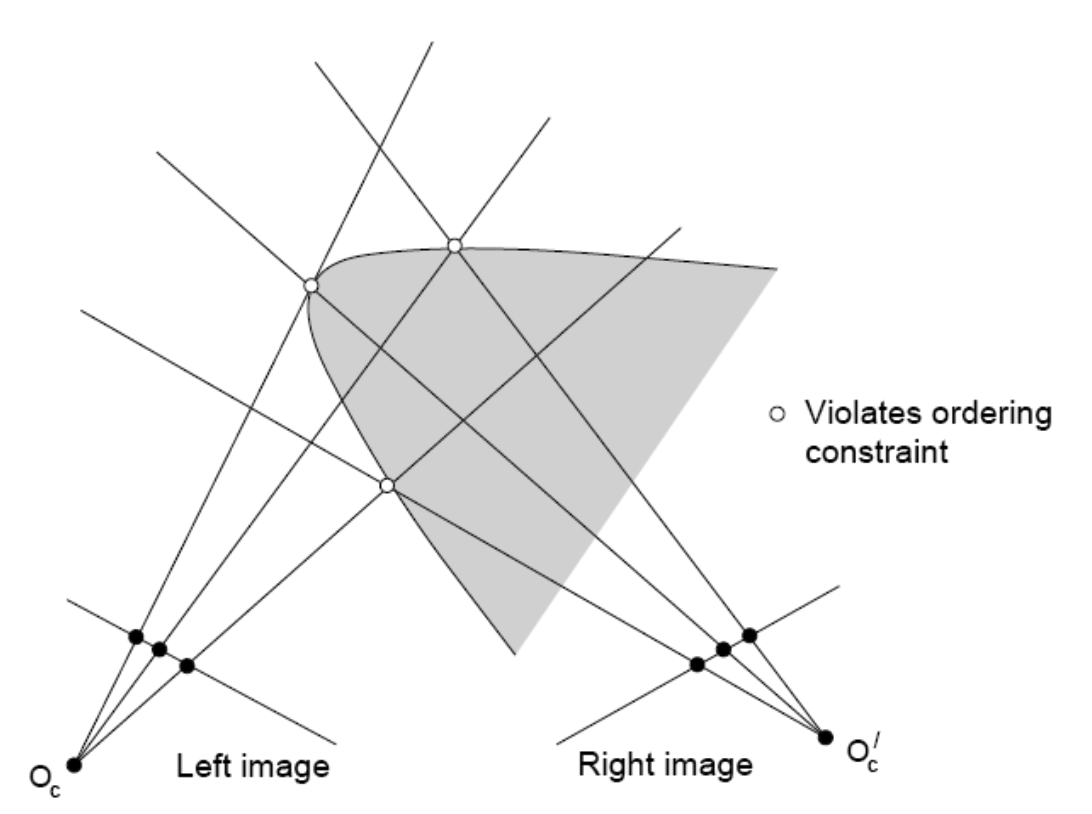
顺序会改变
例外:狭窄的遮挡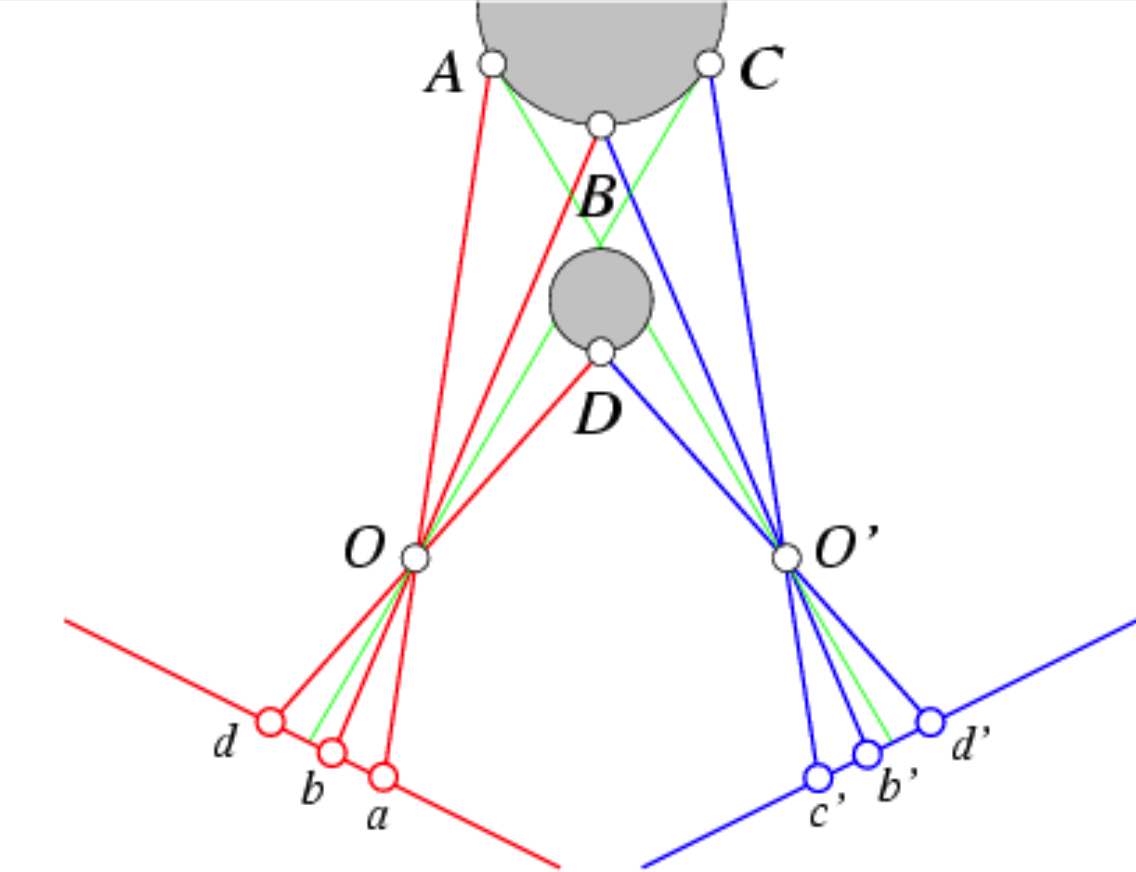
立体的最新技术:
优化算法的两种方法:
- 一次扫描一条线
- 在二维图像中,多扫描一条垂直的线
动态规划公式
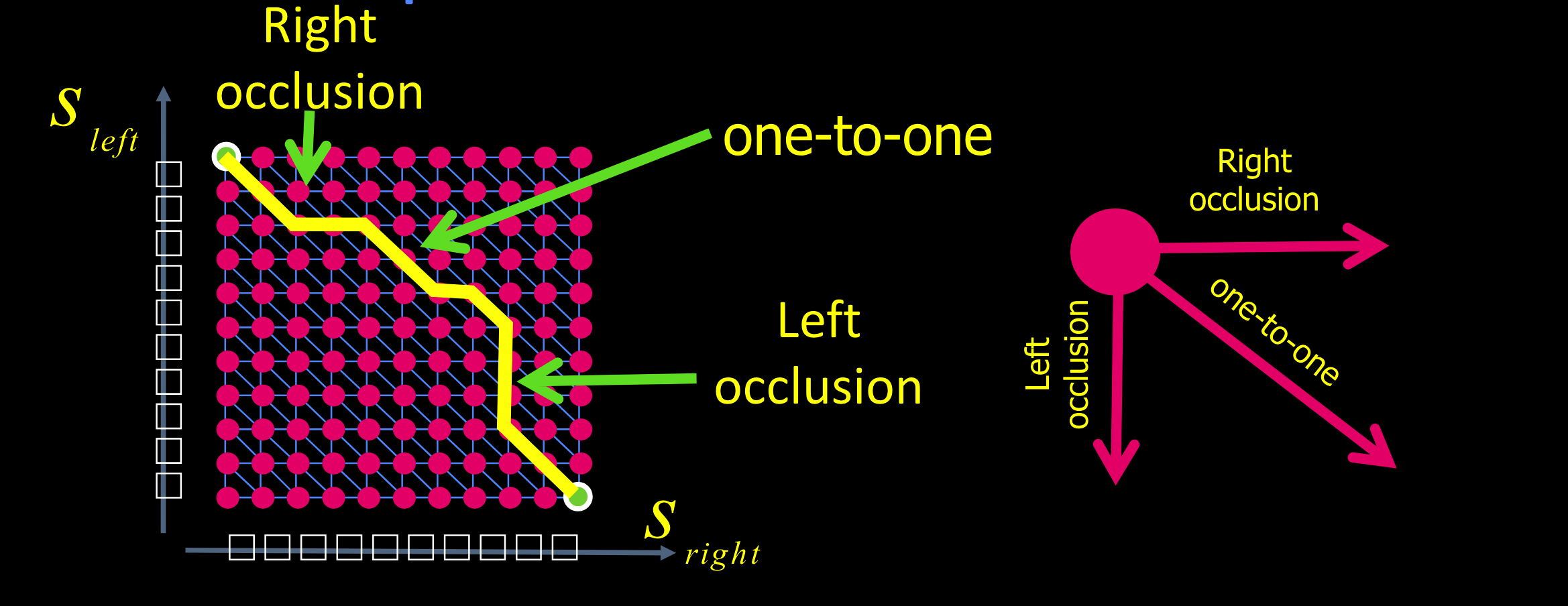
假设已知左上角像素在右图中对应的位置。
- 一对一:两个图中像素点都存在
- 左遮挡:左图可见,而右图不可见
左边的像素被映射到右边同一像素位置,所以看不见 - 右遮挡:相似
立体相似度
什么是一个好的立体相似:
- 数据质量
- 平滑度,相邻像素差异最小
 Data term: $E_\text{ data }=\sum_i\left(W_1(i)-W_2(i+D(i))\right)^2$
Data term: $E_\text{ data }=\sum_i\left(W_1(i)-W_2(i+D(i))\right)^2$
Smoothness term: $E_\text{ smooth }=\sum_{\text{ neighbors }i,j}\rho\left(D(i)-D(j)\right)$
Total energy:$E = \alpha E_{_{\mathrm{data}}}(I_{_1},I_{_2},D)+ \beta E_{_{\mathrm{smooth}}}(D)$
找到一个使总体能量最小的参数。
更好的算法:
将图分割算法应用到立体相似处理。
外置相机校准
几何相机标准
两个方面:
- 任何的世界坐标系
- 从3D到2D的相机坐标系
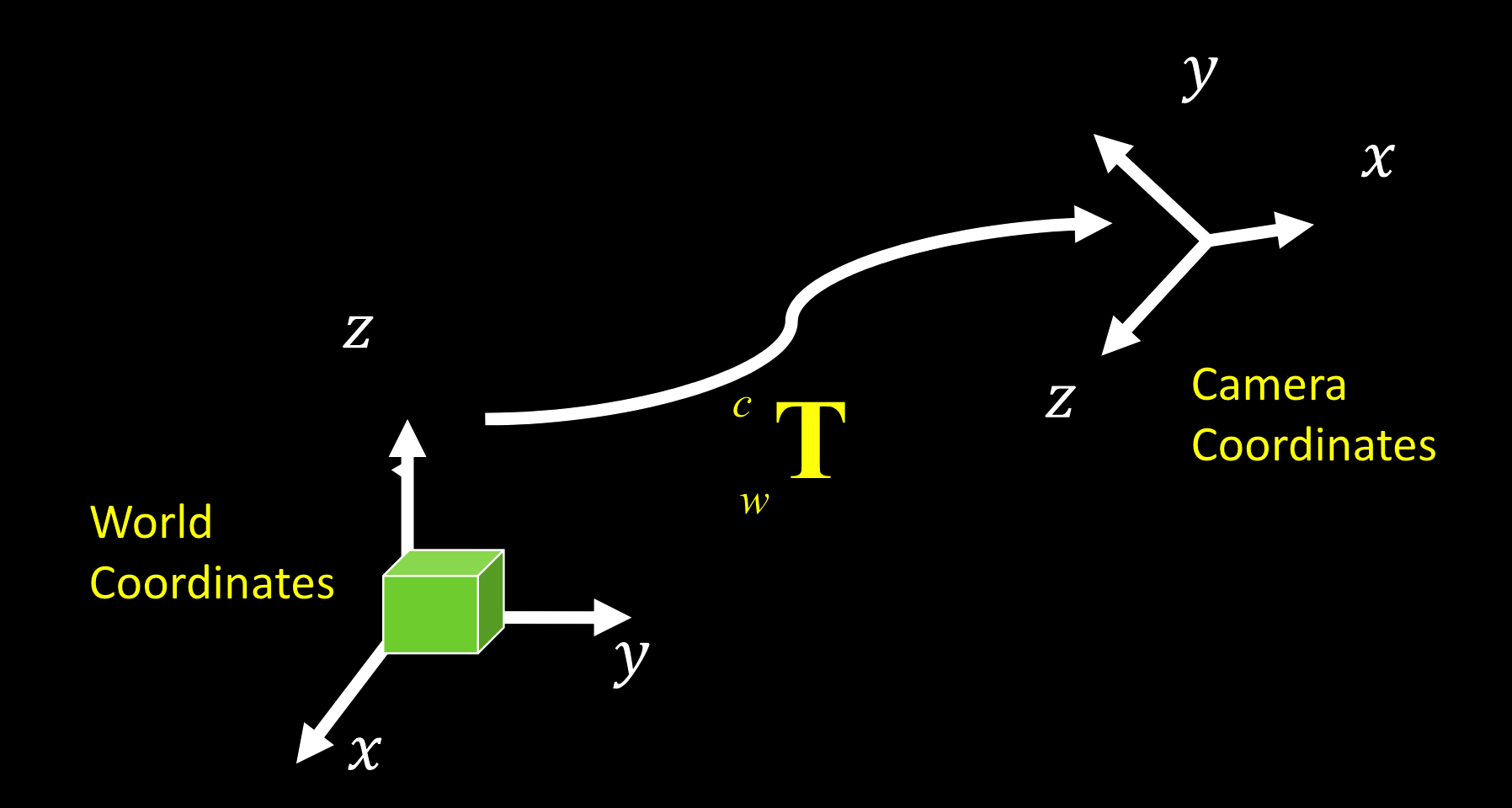 从世界坐标系转换到相机坐标系
从世界坐标系转换到相机坐标系
刚体变换
刚体有6个自由度: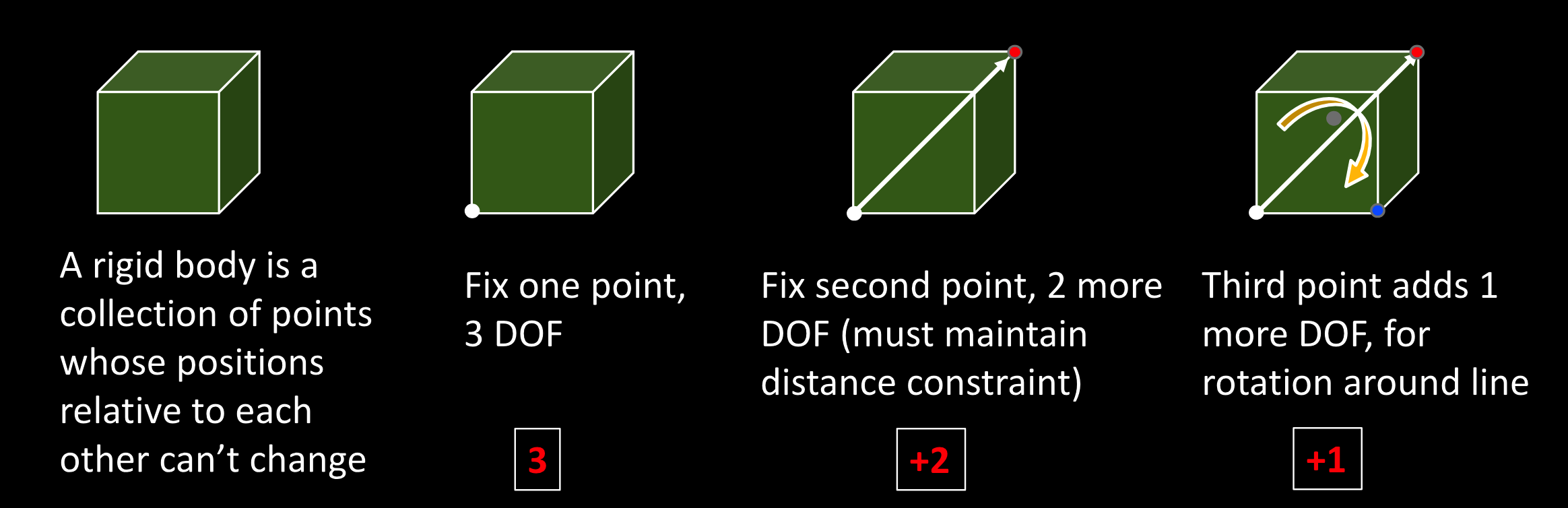
- 一个点可以定位刚体:$(x,y,z)$,三个自由度
- 加一个点,在矢量方向,经纬度,加两个自由度
- 可以旋转,加一个自由度
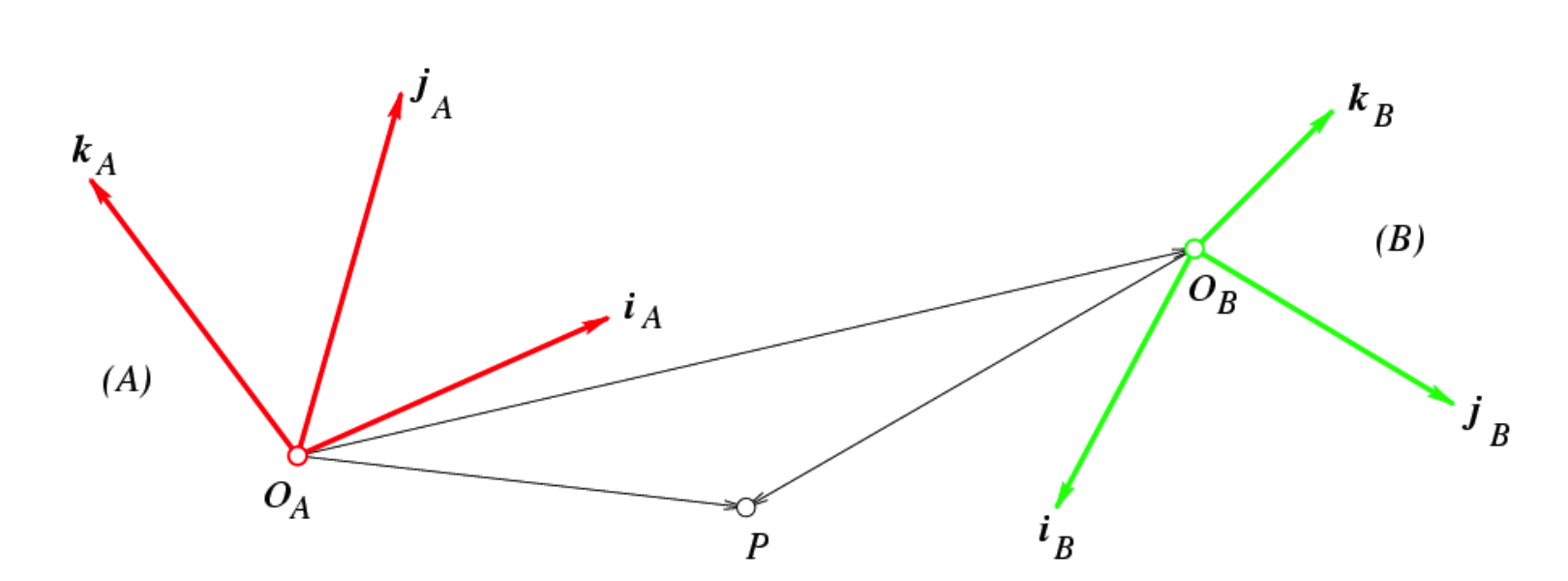
符号 F&P

$^AP=\left(\begin{array}{c}^Ax\\^Ay\\^Az\\\end{array}\right)\Leftrightarrow\overline{OP}=\left(\begin{array}{c}^Ax\cdot\overline{i}\\\end{array}\right)+\left(\begin{array}{c}^Ay\cdot\overline{j}\\\end{array}\right)+\left(\begin{array}{c}^Az\cdot\overline{k}\\\end{array}\right)$
- 上标代表所在坐标系
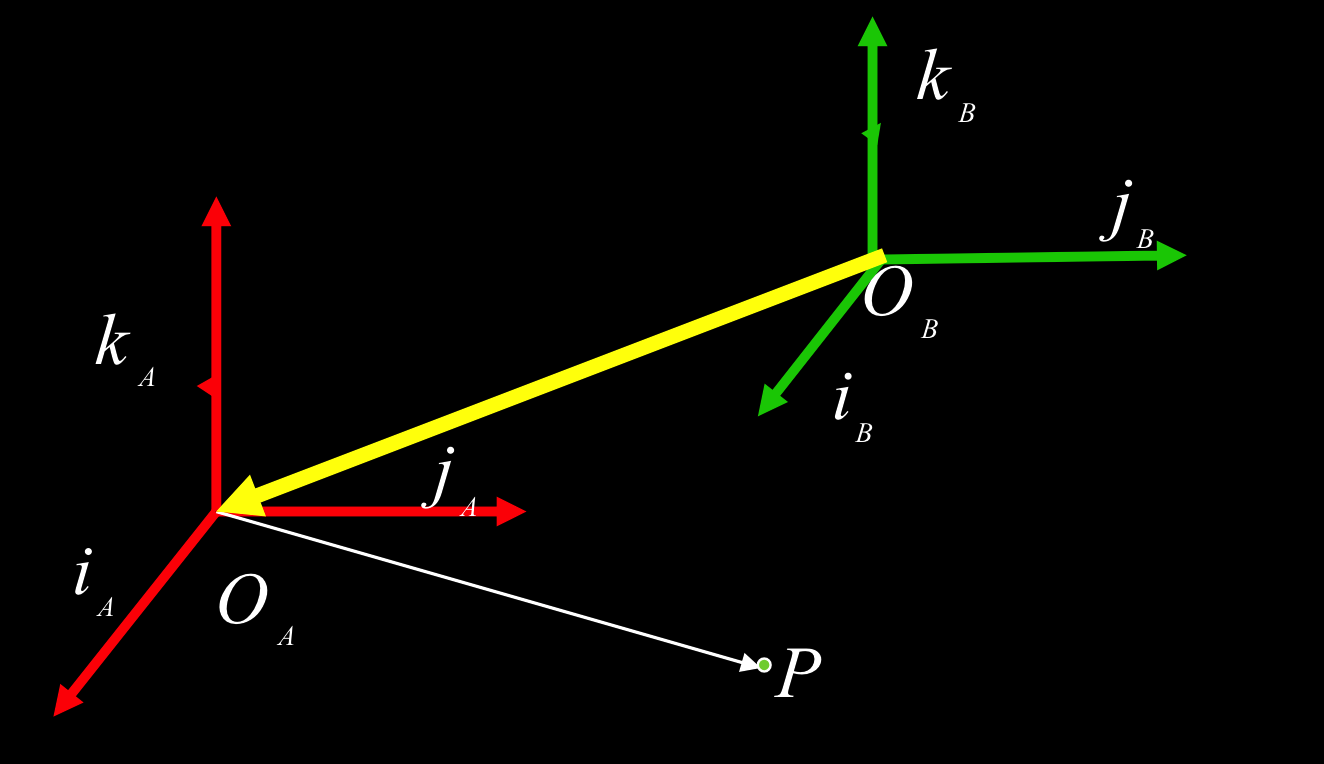
坐标转换:已知了两个坐标原点之间的向量
$^BP=^AP+^B\left(O_A\right)$
或
$^BP=2^B\left(O_A\right)+2^AP$
就是向量加法
齐次坐标法:
\begin{split}\left[\begin{array}{c}^BP\\1\end{array}\right]=\left[\begin{array}{cc}K^BO_A\\0^T&1\end{array}\right]\left[\begin{array}{c}^AP\\1\end{array}\right]\end{split}
变换可逆
旋转
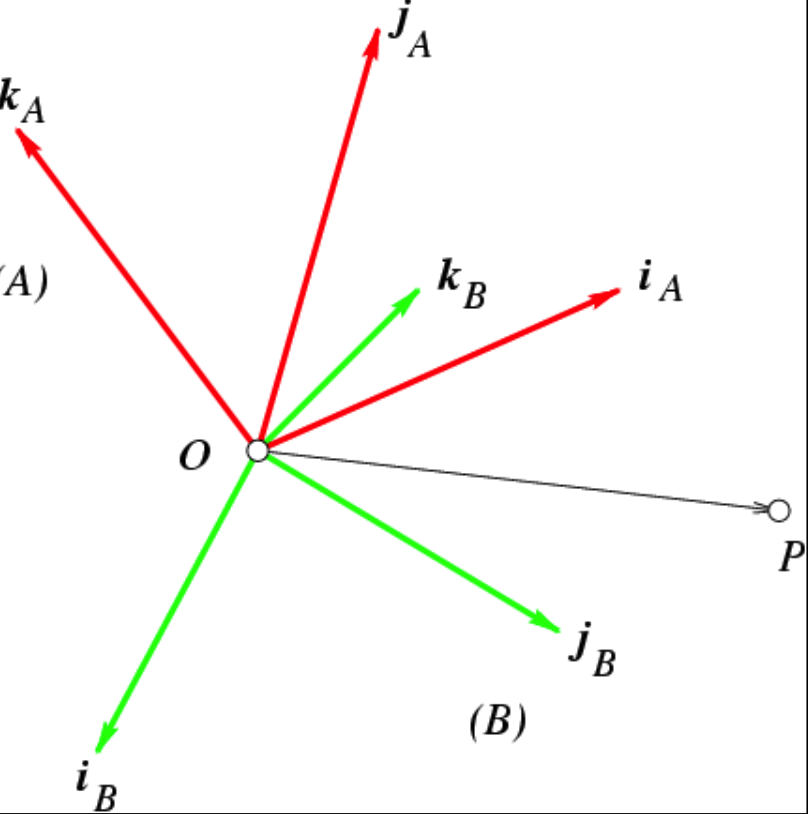
坐标原点重合
$\overrightarrow{OP}=\begin{pmatrix}i_A&&j_A&&k_A\end{pmatrix}\left(\begin{array}{c}A\\X\\\\A\\y\\\\A\\z\end{array}\right)=\begin{pmatrix}i_B&&j_B&&k_B\end{pmatrix}\left(\begin{array}{c}B\\X\\\\B\\z\end{array}\right)$
转换公式:基变换
$^BP=_A^BR^AP$
$_A^BR$: 在B的坐标系中描述A
旋转不可交换
刚体变换
$^BP=\frac BAR^AP+^BO_A$
将坐标点旋转到B坐标系,加上加上A坐标系在B坐标系中的偏移量。
从世界坐标到相机坐标的转换: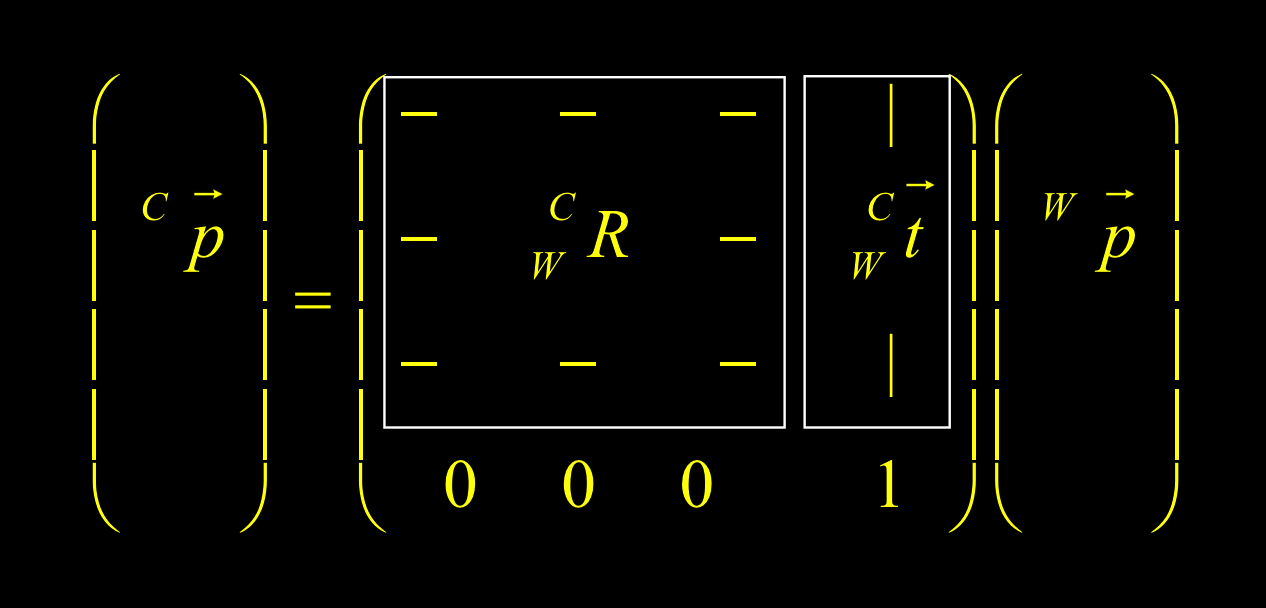
相机内部校准
从3D相机坐标到2D图像坐标
实际的参数
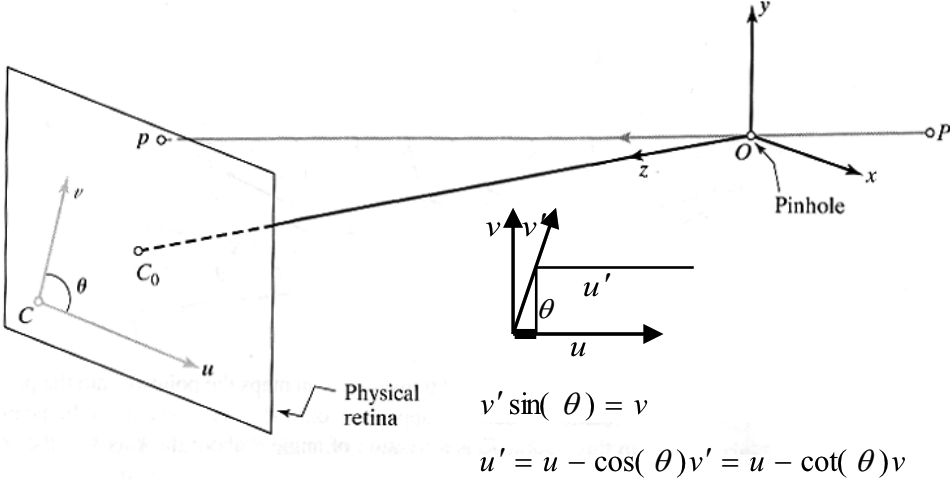
\begin{split}&u = \alpha \frac{x}{z}-\alpha \cot(\theta ) \frac{y}{z}+u_{_0}\\&\nu=\frac\beta{\sin(\theta)}\quad\frac{y}z+\nu_0\end{split}
- 光学中心不在图像中间
- 坐标系不垂直
- 长宽像素缩放比不相同
改善转换方程:
齐次坐标法:
\begin{split}
\begin{pmatrix}z^*u\\\\z^*\\\\nu\\\\z\end{pmatrix}=\begin{pmatrix}\alpha&-\alpha\cot(\theta)&u_0&0\\\\0&\frac{\beta}{\sin(\theta)}&\nu_0&0\\\\0&0&1&0\end{pmatrix}\begin{pmatrix}x\\\\y\\\\z\\\\1\end{pmatrix}\\\vec{p^{\prime}}=K^c\vec{p}
\end{split}
5个自由度: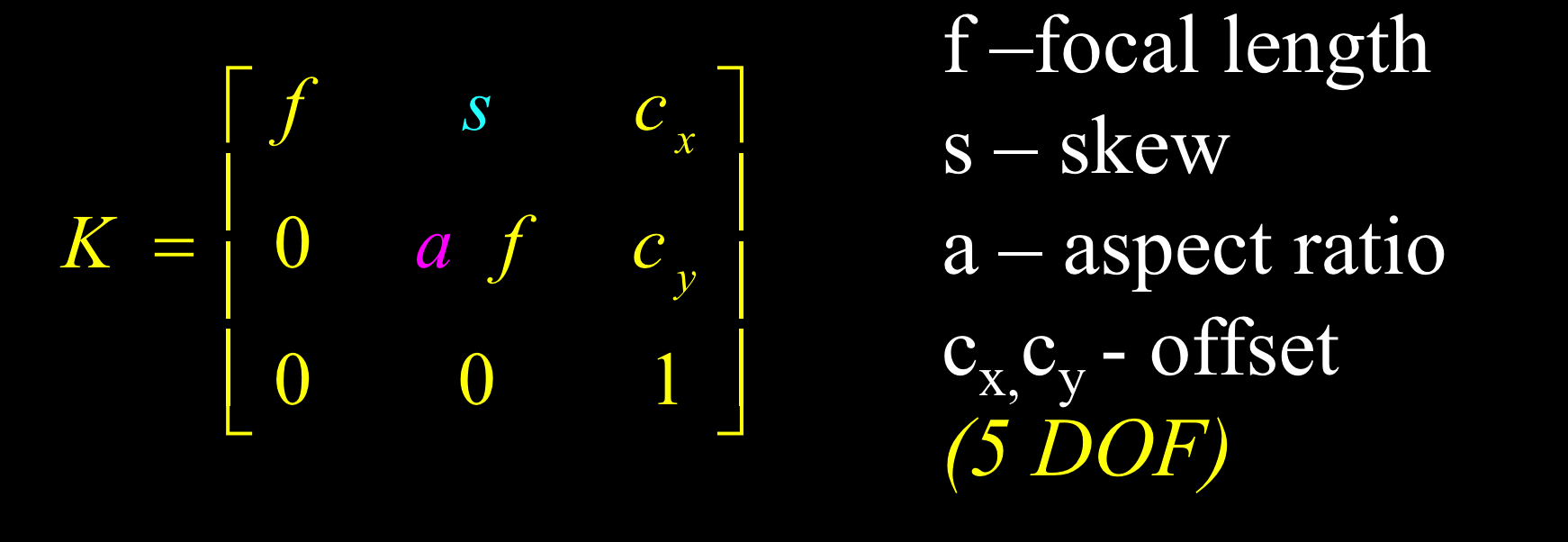
结合内部参数和外部参数
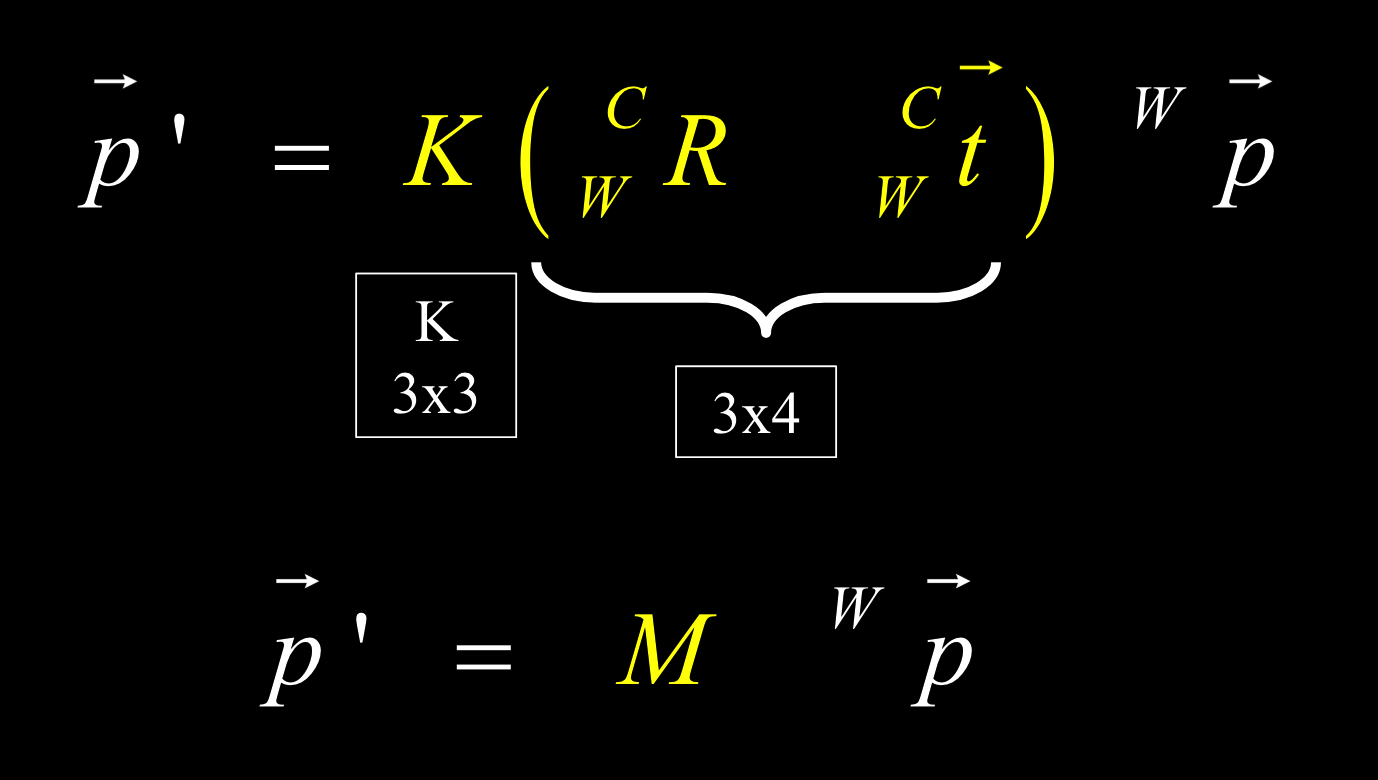
相机的全部参数
11个自由度:
使用光谱校准相机
校准方法
利用已知点进行校准
切割法校准:
获取一些已知点,建立世界坐标系,测量设置点的坐标在世界中的相对位置,然后回恢复校准坐标。
齐次校准
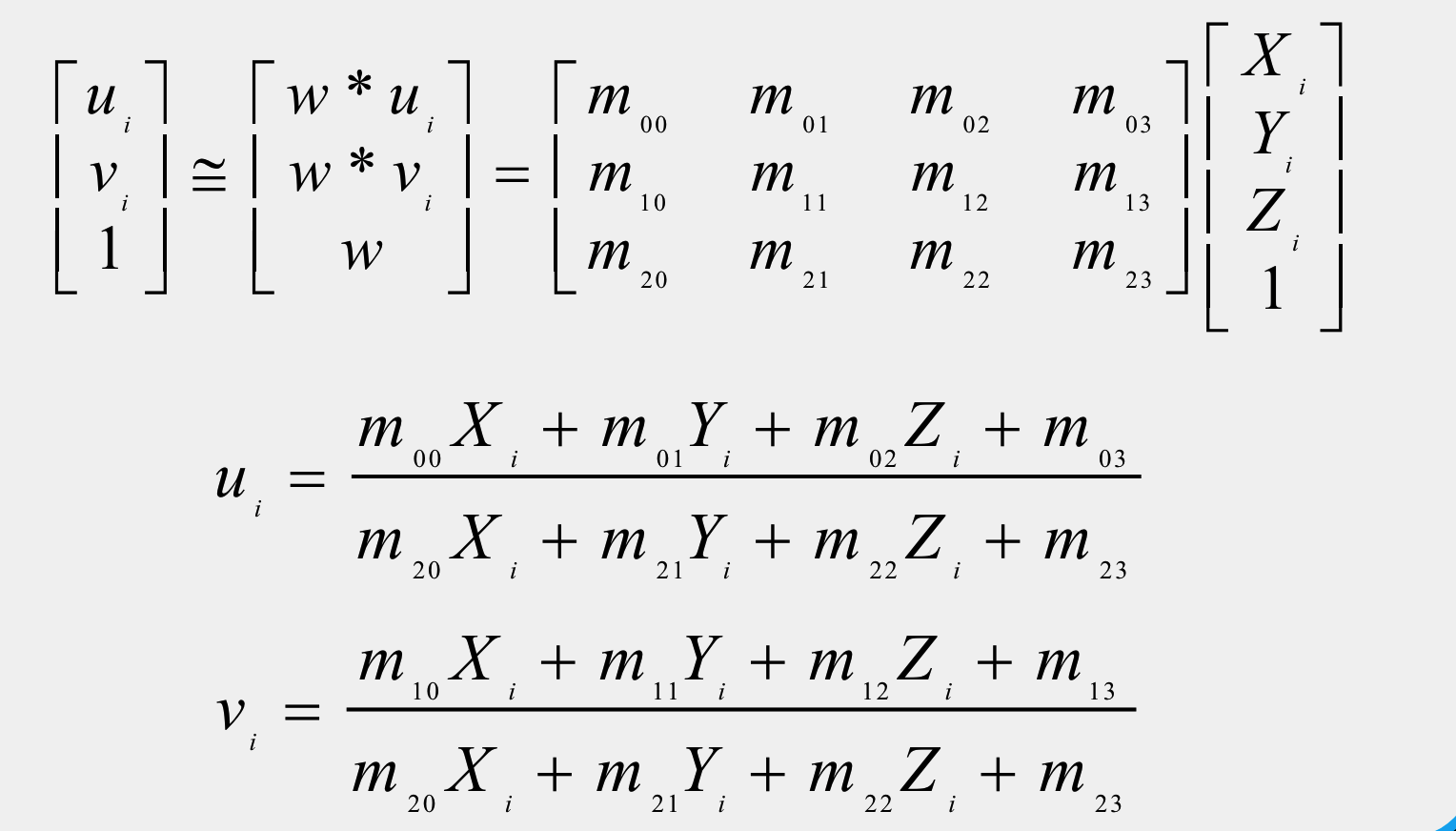
坐标系下的直线校准:
SVD分解:奇异值分解


非齐次方法
误差函数
$\text{minimize }E=\sum_id(x_i^\prime,\hat{x}_i^\prime)$
如果有复杂的映射:
$\min_\mathbf{M}\sum_id(x_i^{\prime},\mathbf{MX}_i)$
用参数$M$修正
黄金标准算法:
标准归一化:
$\tilde{\mathbf{X}}_i=\mathbf{U}\mathbf{X}_i\tilde{\mathbf{x}}_i=\mathbf{T}\mathbf{x}_i$
$\min_\mathbf{M}\sum_id\left(\tilde{\mathbf{x}}_i,\tilde{\mathbf{M}}\tilde{\mathbf{X}}_i\right)$
$\mathbf{M}=\mathbf{T}^{-1}\tilde{\mathbf{M}}\mathbf{U}$
类似特征向量,转换为标准正交基上
从M中找3D相机中心
直接的方法:
如果能找到一个点$C$, 使得$\textbf{M C = 0}$,就是相机中心。
原理:
$\mathbf{X}=\lambda\mathbf{P}+(1-\lambda)\mathbf{C}$
$\mathbf{x}=\mathbf{M}\mathbf{X}=\lambda\mathbf{M}\mathbf{P}+(1-\lambda)\mathbf{M}\mathbf{C}$
简单的方法:
$\mathbf{C}=\begin{pmatrix}-\mathbf{Q}^{-1}\mathbf{b}\\\\1\end{pmatrix}$
多平面校准
目前最常使用的:
优点:
- 只需要一张纸
- 不需要知道相机内部参数
- 代码是公开的
多视角
图像到图像投影
2D变换: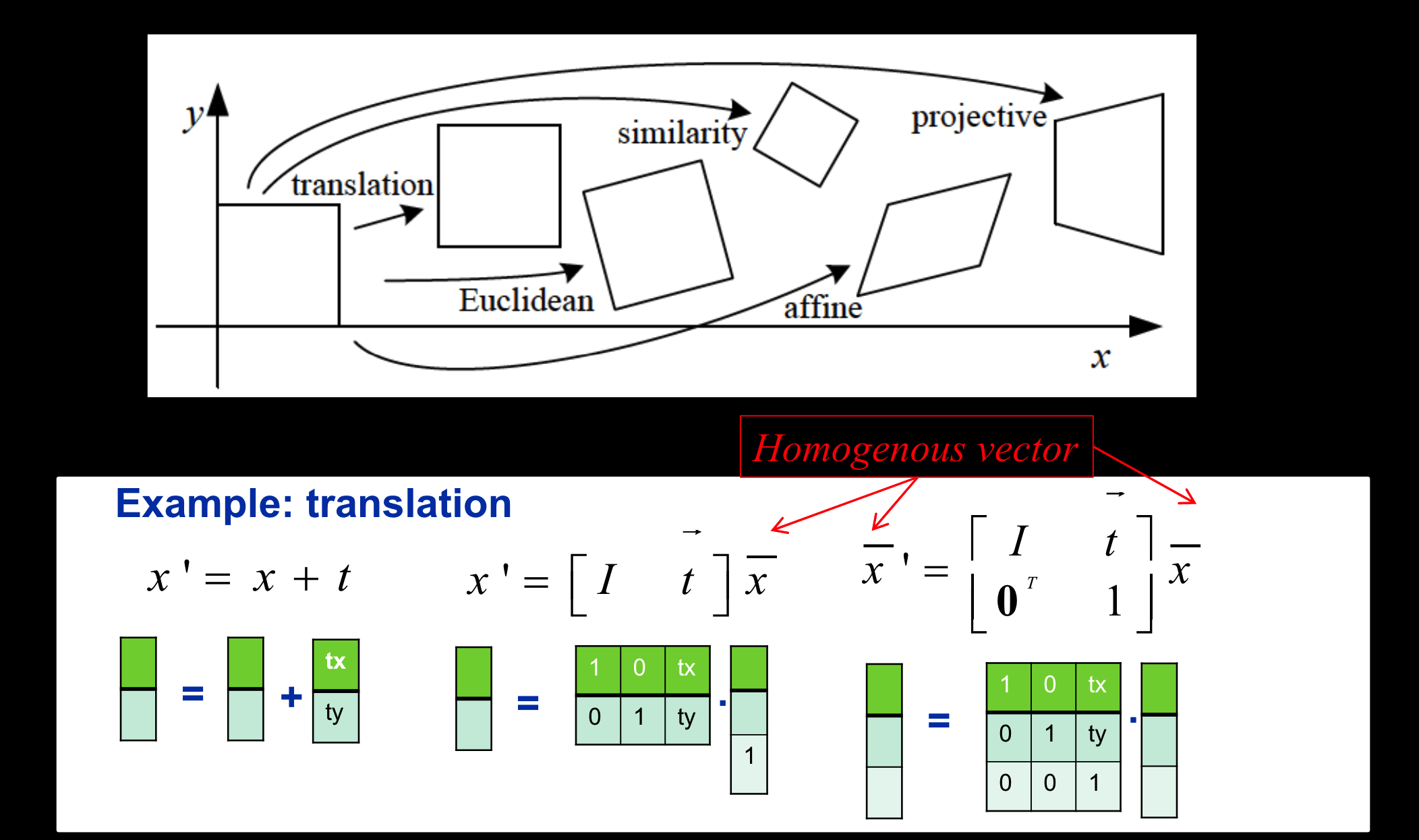
特殊投影变换:
变换: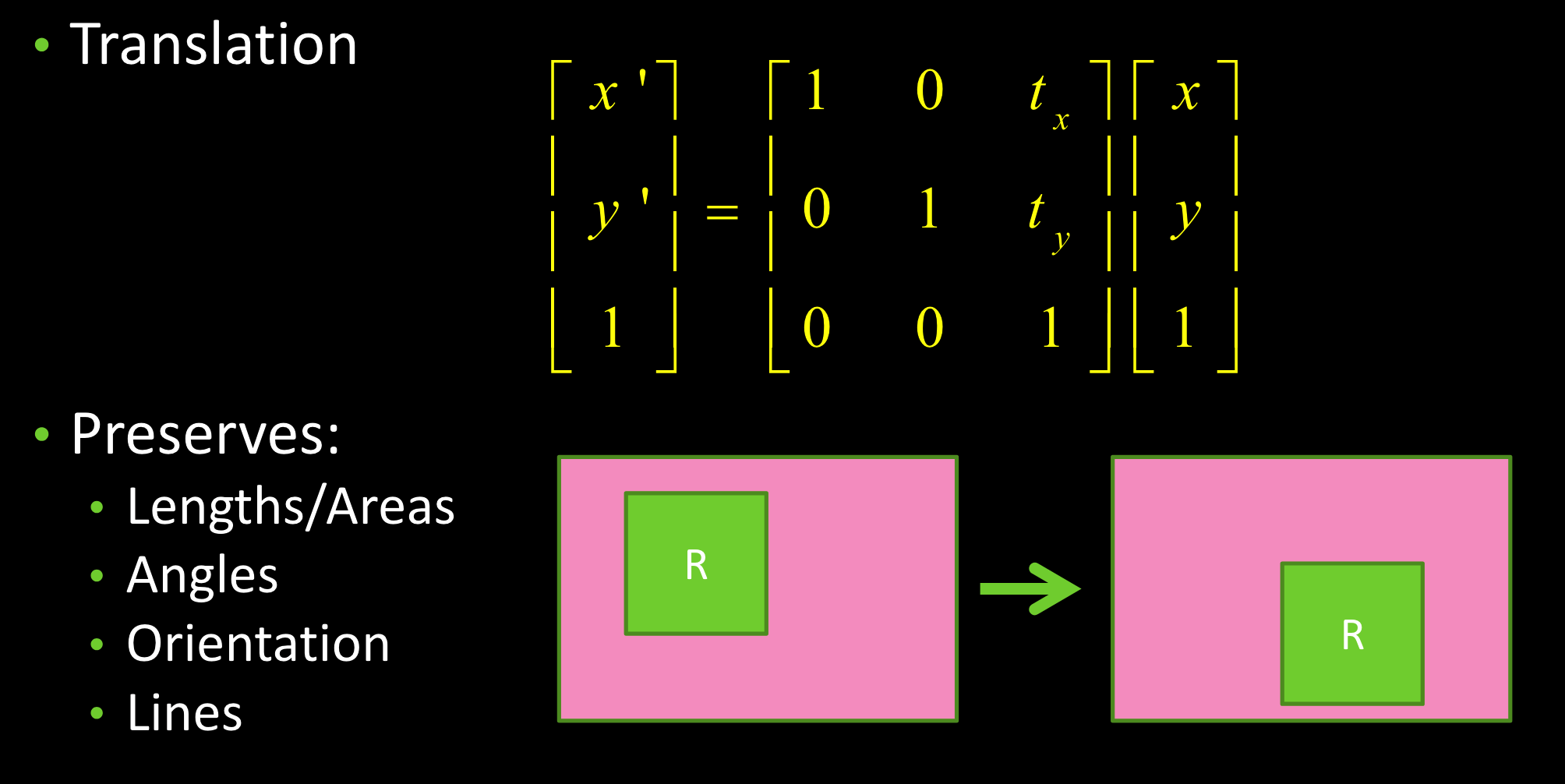
刚体变换: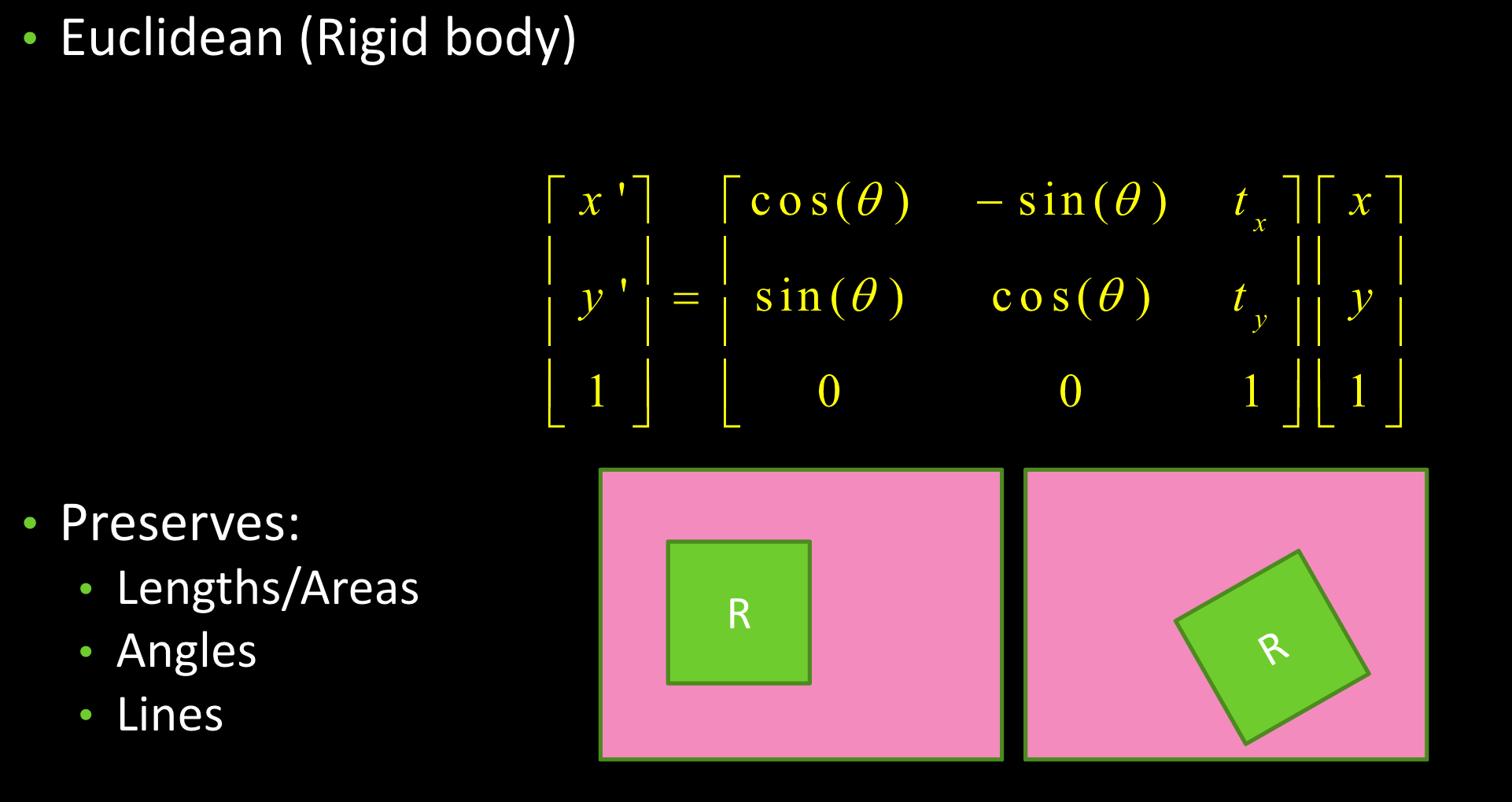
相似变换: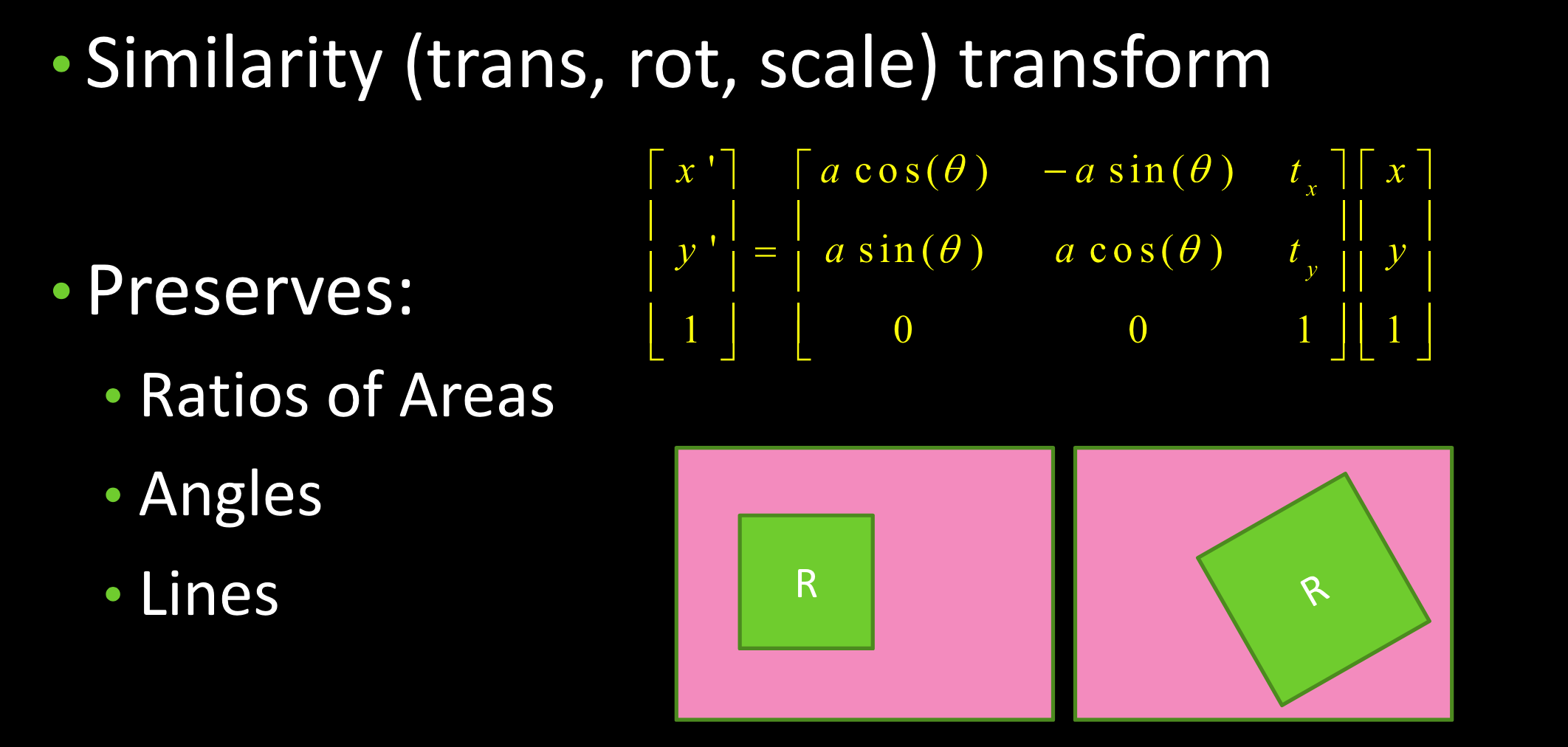
仿射变换:Affine transform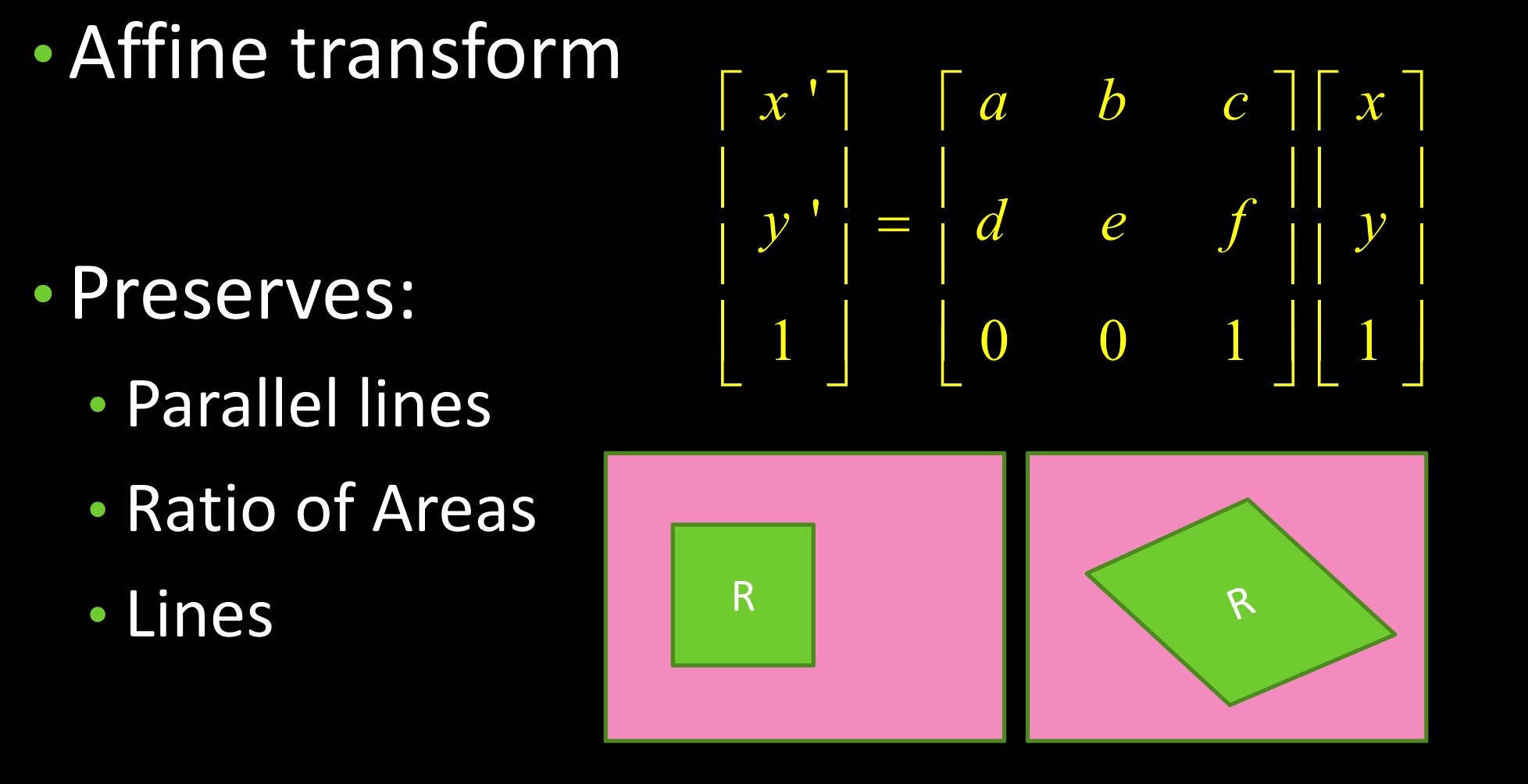
一般投影变换: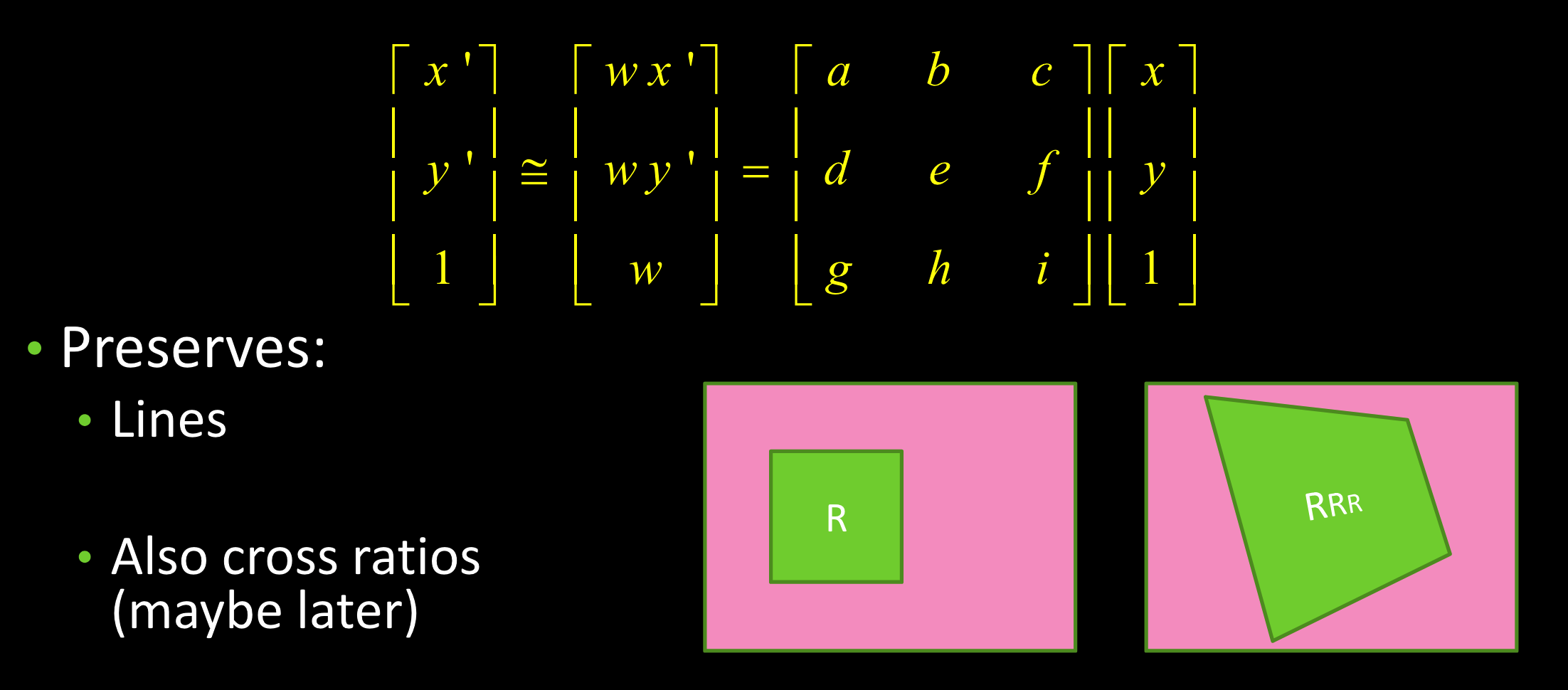
马赛克
平面图: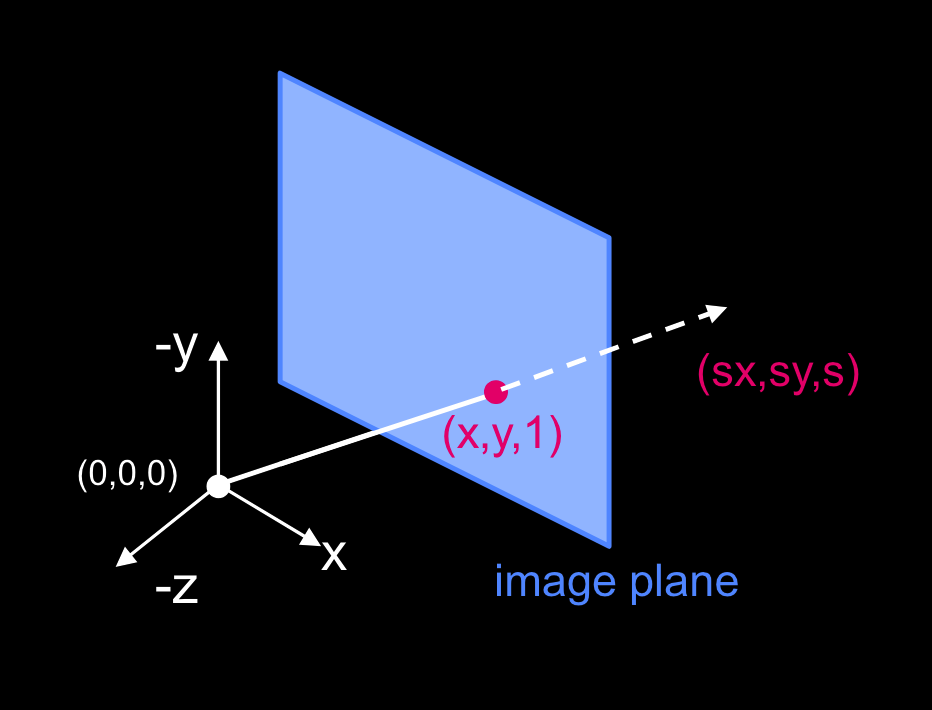
射线上任一点,投影到平面上,都是交点重合。
图像重影
相机中心相同,拍摄了两张照片: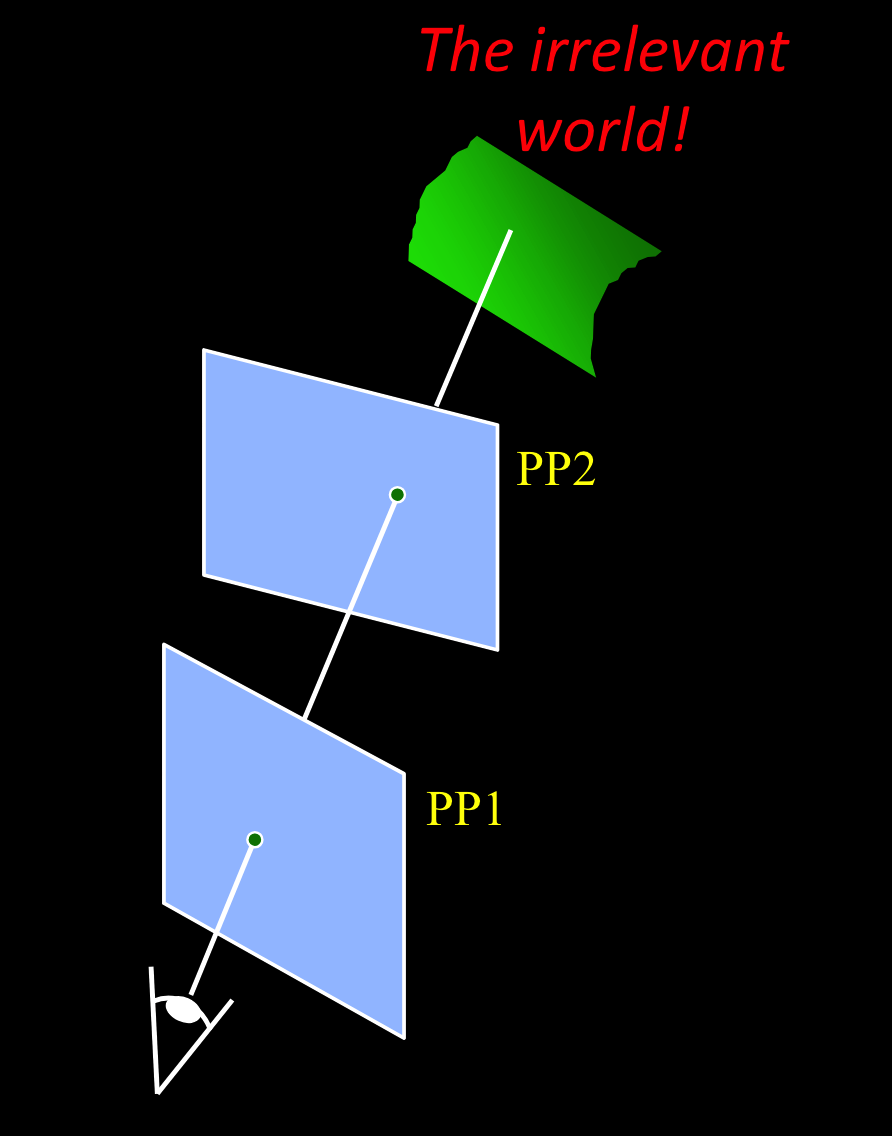
全景图像:
保存相机中心不变,移动水平角度,拍摄照片,重合起来就是全景图像。
自然几何:
将图像投影到大平面上,组成全景图像,重叠部分混合。
相同位置的不同坐标:
关键是求解: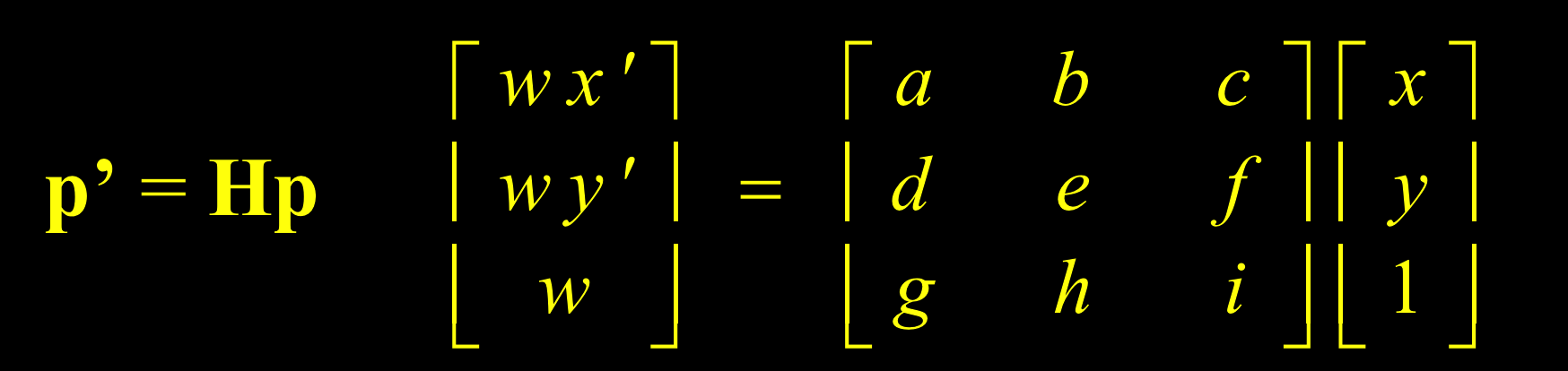
转换图像(图像扭曲):是一种插值
全景图像方法:可以用于去除图像中元素
3D图像
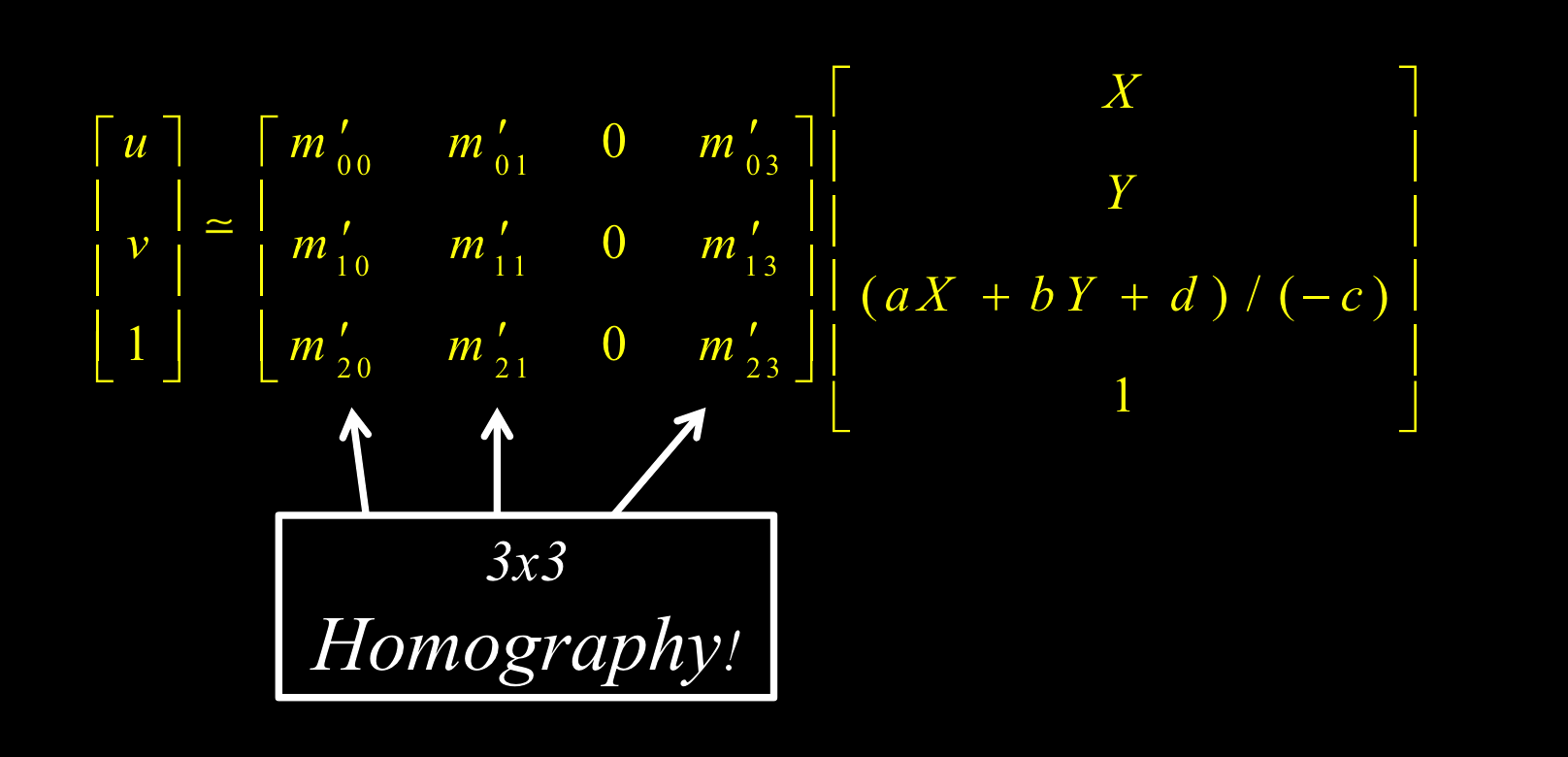
两种图像扭曲方法
向前扭曲:错误方式
像素离散化时,某一点的像素位置移动了,需要分散给其他像素。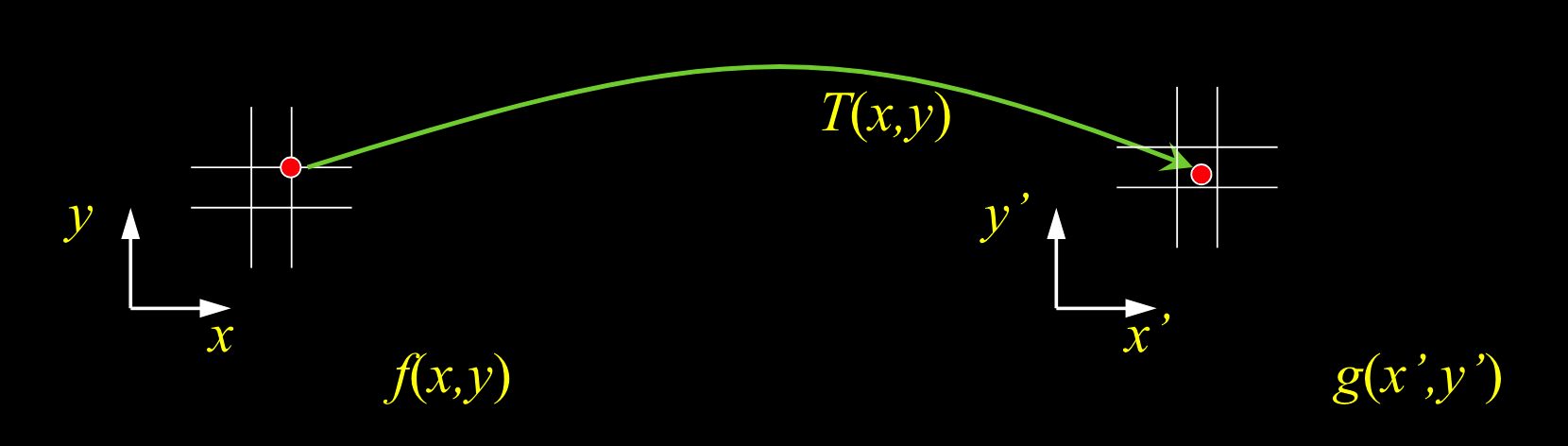
反向扭曲:
中间像素的插值法: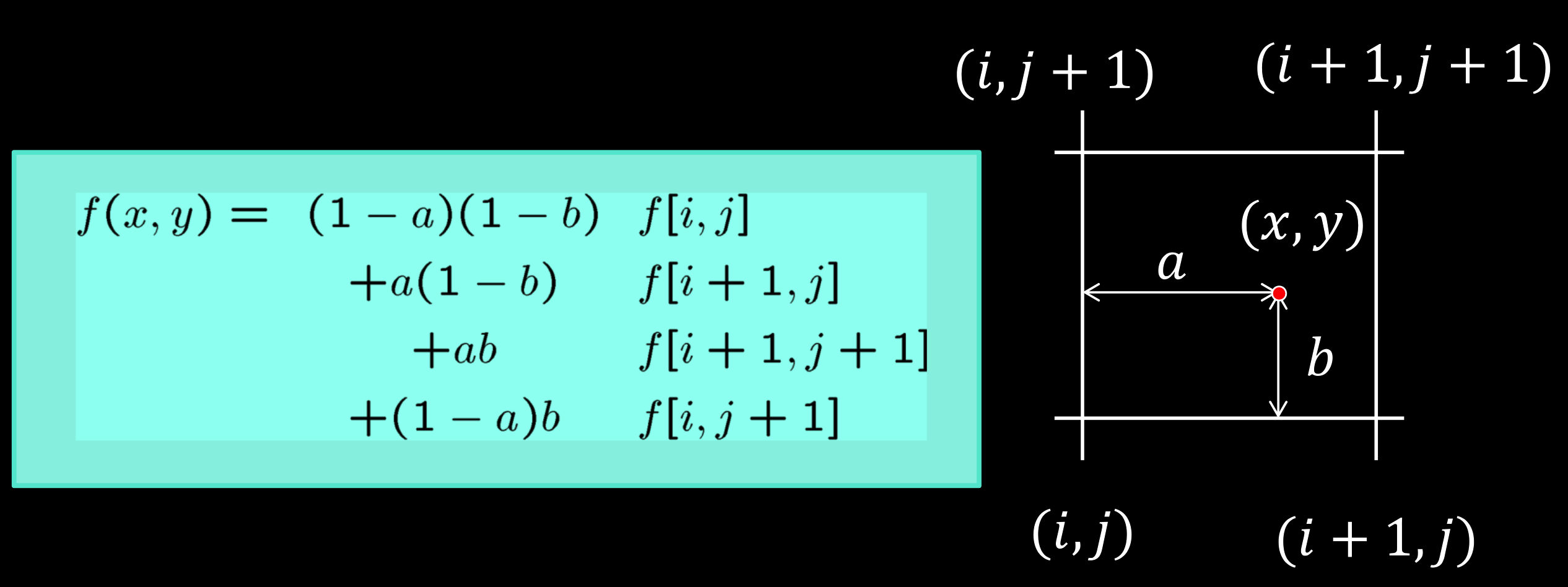
投影几何
基本平面知识
基本矩阵
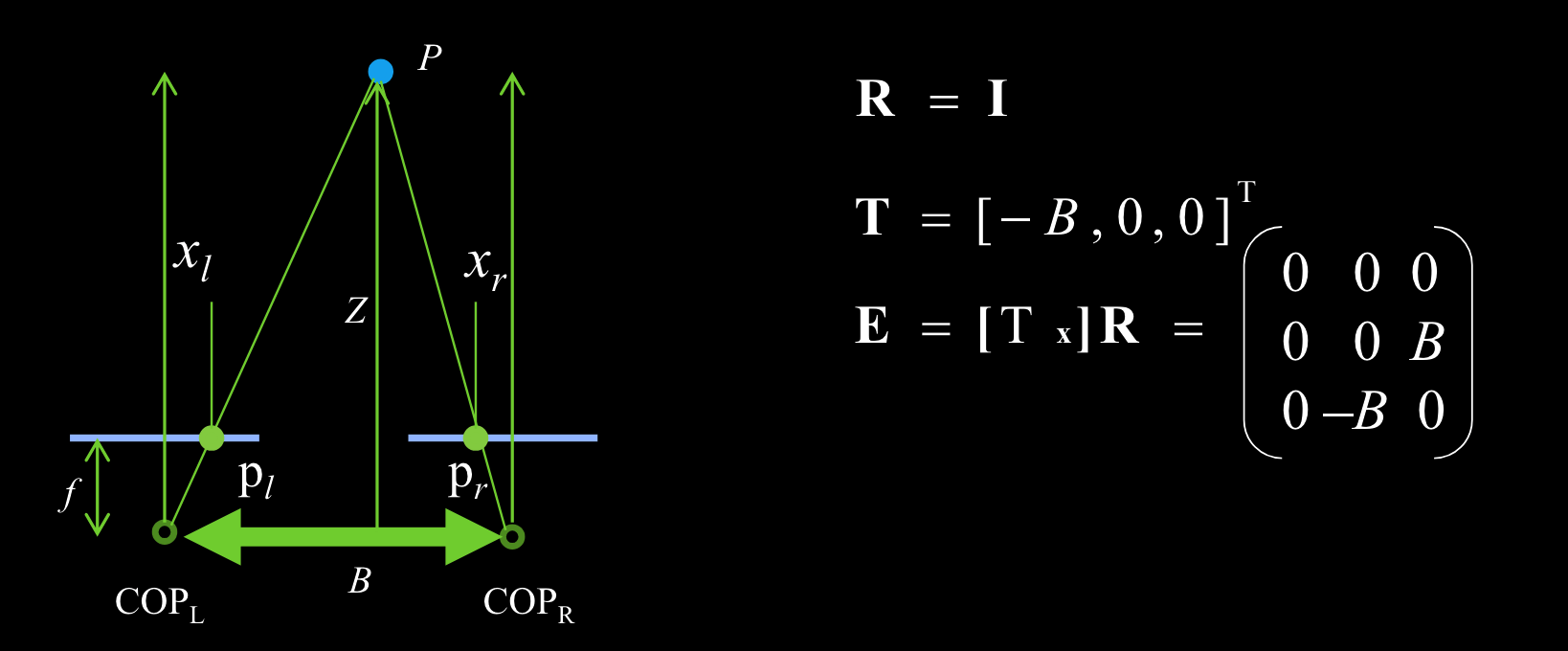
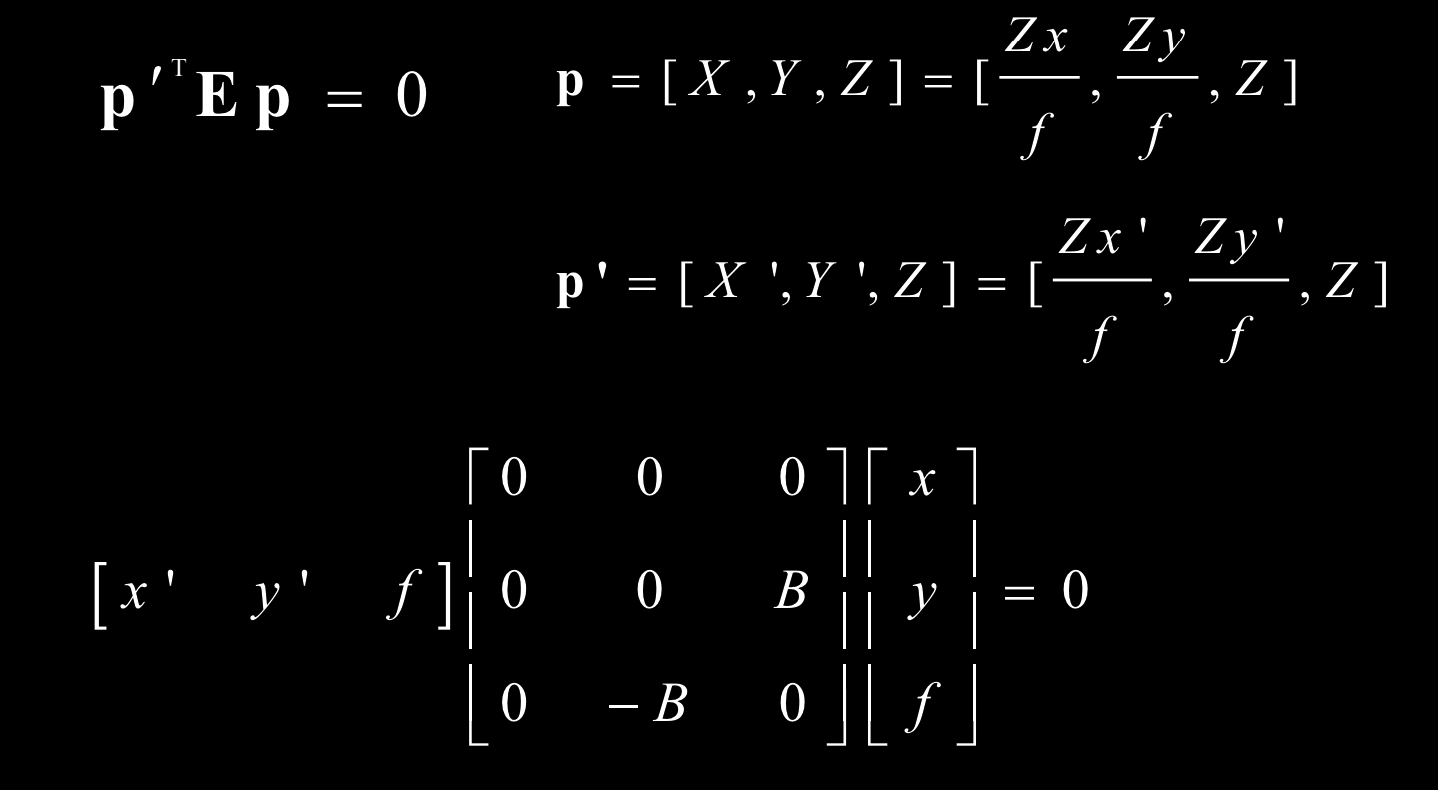

基础矩阵
弱校准