计算机视觉概论 计算机视觉的图像处理
更新历史
- 24.04.27:初稿
系列
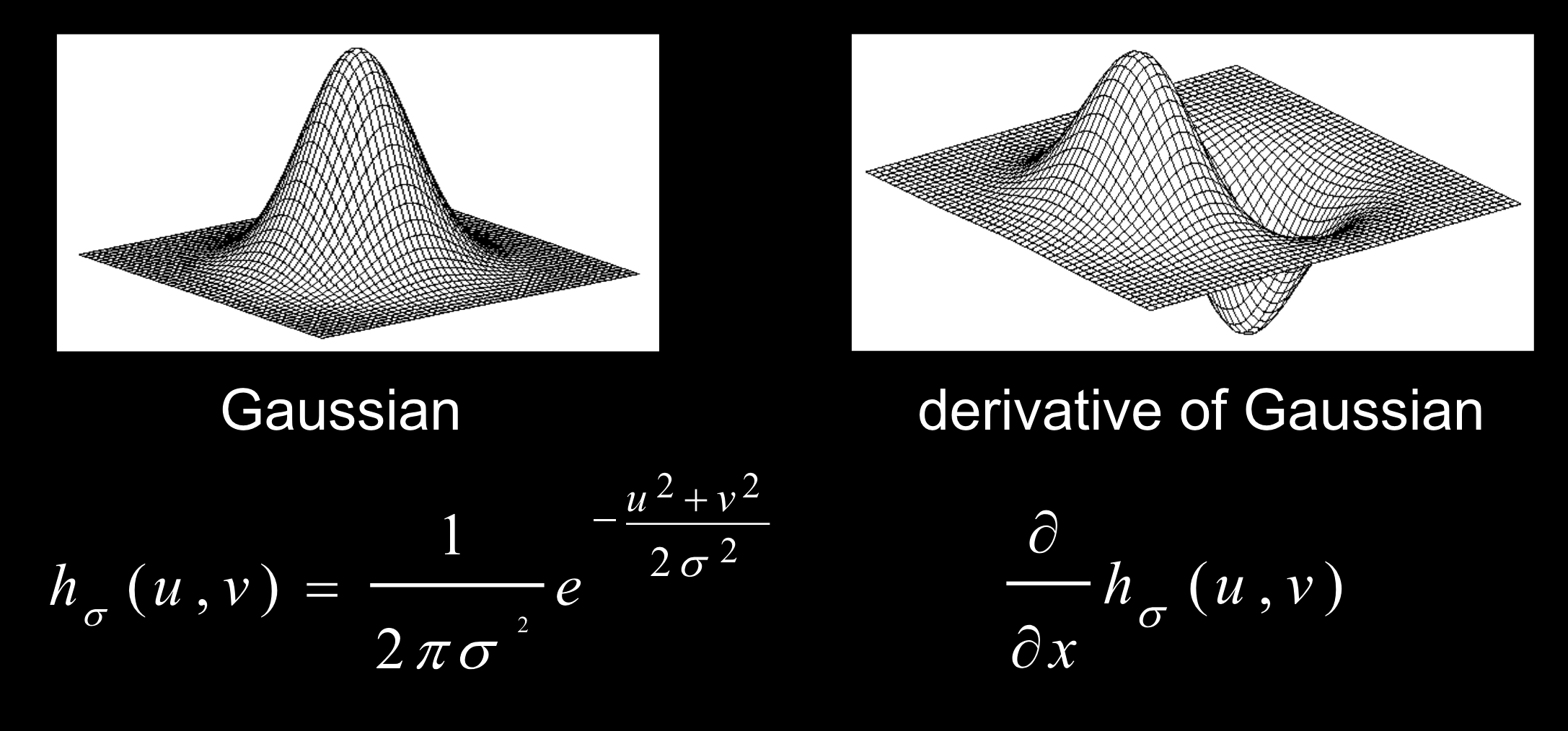
图像作为函数
理解图像函数

通常我们认为图像就是看到的东西,实际上,图像是一个函数$I(x, y)$,值为像素值。
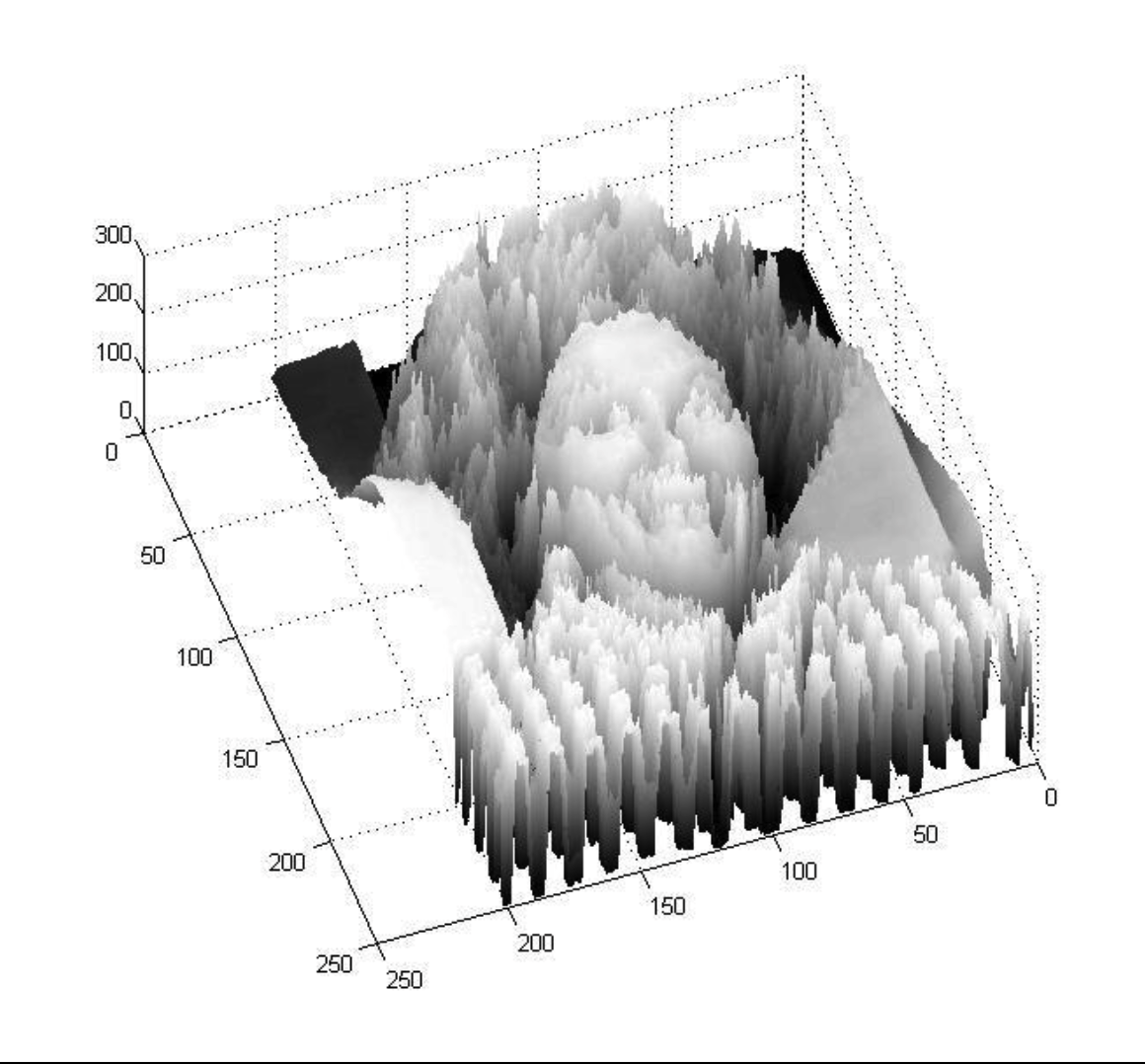
上面两种形式是一个相同的函数,只是展示方式不同。
对图像做平滑处理,函数变为: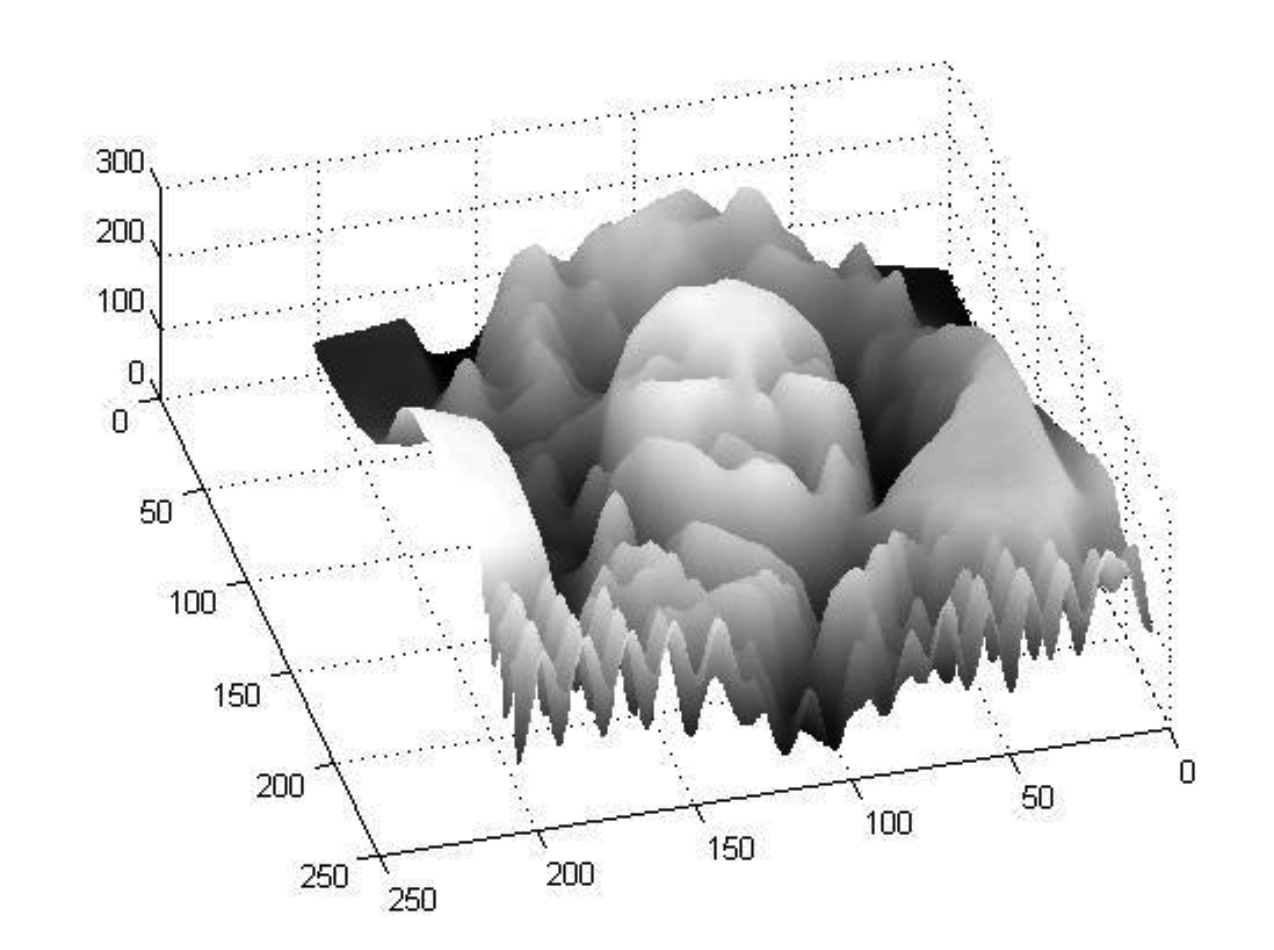
对图像做模糊处理,函数变为: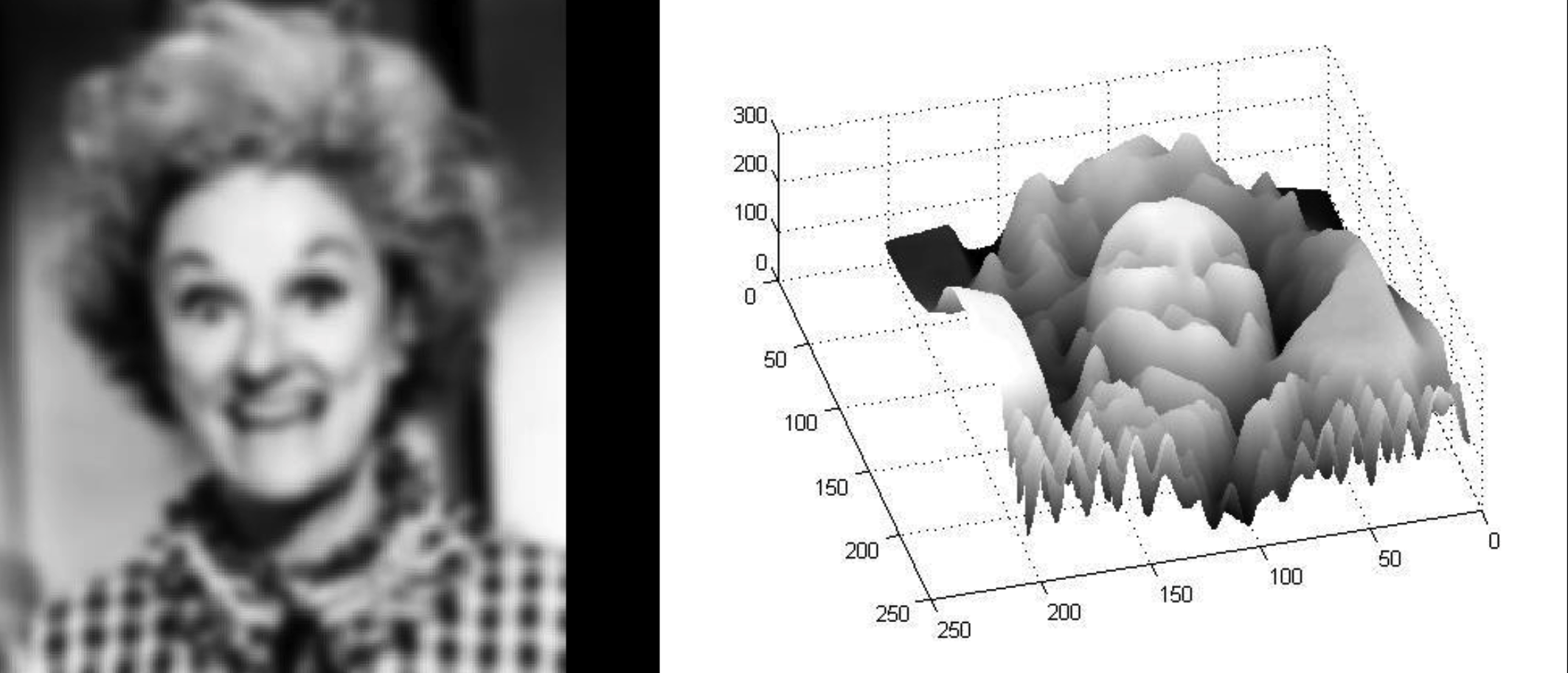
图像函数
$f(x, y)$:是图像在点$(x, y)$处的光强度或值
限制$x$,$y$的范围,以及强度的范围:$f:[a, b] x[c, d] \rightarrow[\min , \max ]$
图像定义:$x$为列,$y$为行, 原点在图像左上角
图像范围不是0-255,而是0-1,0为黑,1为白,最小值为黑色,最大值为白色,甚至可以存在负值图像。
黑白定义来源光的强度,值越大,强度越高,为白色
彩色图像:
\begin{split}
f(x, y)=\left[\begin{array}{l}
r(x, y) \\
g(x, y) \\
b(x, y)
\end{array}\right]
\end{split}
每个像素为一个向量,RGB:值分别为,红,绿,蓝的颜色强度。
真实的菲利斯
这与眼睛看到的图像是相同的函数。
数字图像
Sample:采样,对2D图像进行采样, 即像素
Quantize:量化,用一个有限数量的位数来表示它
量化使用浮点图像?
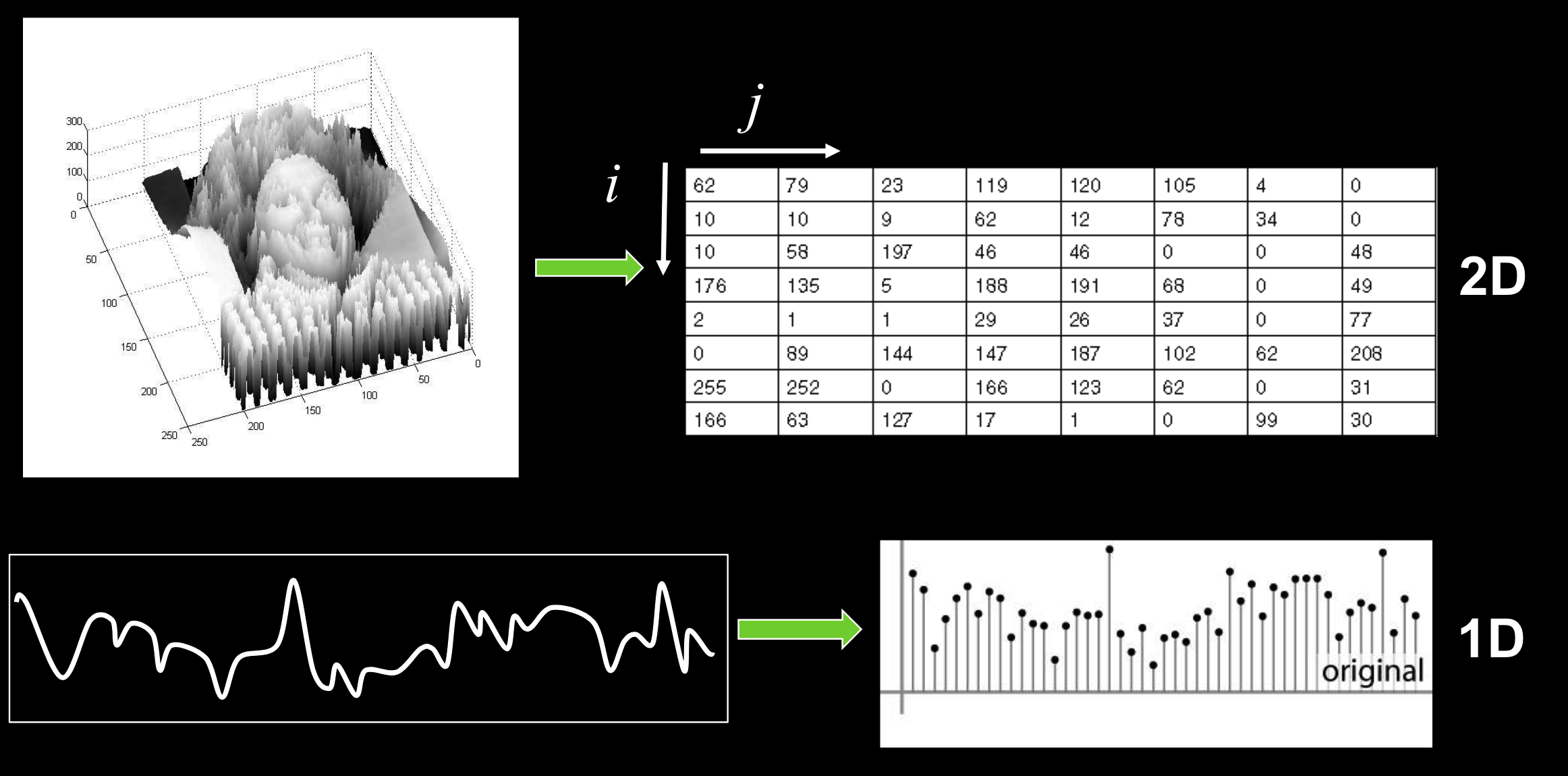
图像由$(x,y)$确定,而计算中的$(i,j)$,为行,列值,与$x$,$y$,相反。
有时图像也可用一维信号表示。
图像是矩阵存储
课程使用的MATLAB,目前多使用OpenCV,所以不记笔记。
图像噪声
$\vec{I}^{\prime}(x, y)=\vec{I}(x, y)+\vec{\eta}(x, y)$

椒盐噪声: 产生黑白像素点

脉冲噪声: 产生白色像素点

高斯噪声或正态分布噪声: 产生某些正态分布或某些高斯分布独立同分布的值
Sigma 对高斯噪声的影响

不同sigma的图像函数。
- 噪声有什么意思?
“零”
对于负值图像,错误的想法是0是黑色,255是白色,黑色白色,只是值范围内的最小值与最大值,0代表的是两者之间,灰色。非常小的sigma,是一个恒灰函数。 - 不同的sigma对应不同的图像值范围,(0-255), sigma5是合理的。
过滤和噪声
如何过滤高斯噪声
采用平滑图像,在一维像素中,周围像素平均值设置为当前像素值,可以消除噪声。
平均值的假设
- 真实像素值可能与周围像素值相近
- 每个像素的噪声相互独立
意味着如果取噪声的平均值,噪声将为0
加权移动平均线
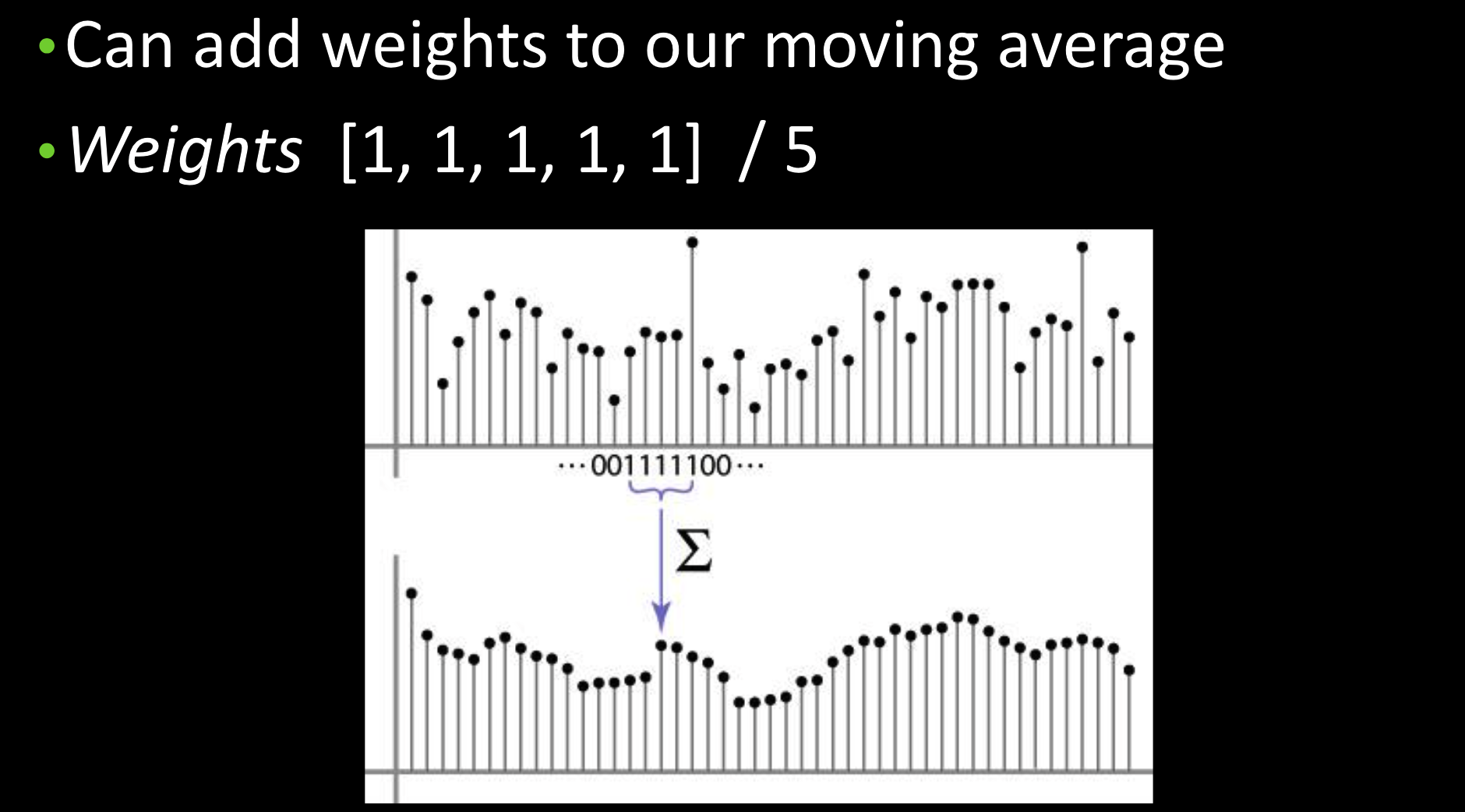
非均匀权重:距离像素越近,权重越大,可以使图像更平滑。
2D 移动平均线
简单的平均权重

移动平均之后的结果
相关过滤
上述过滤为统一权重过滤,公式为:
核的size: 2 * k + 1;
$G[i, j]=\frac{1}{(2 k+1)^2} \sum_{u=-k}^k \sum_{v=-k}^k F[i+u, j+v]$
非均值权重的公式为:
$G[i, j]=\sum_{u=-k}^k \sum_{v=-k}^k H[u, v] F[i+u, j+v]$
平均滤波器
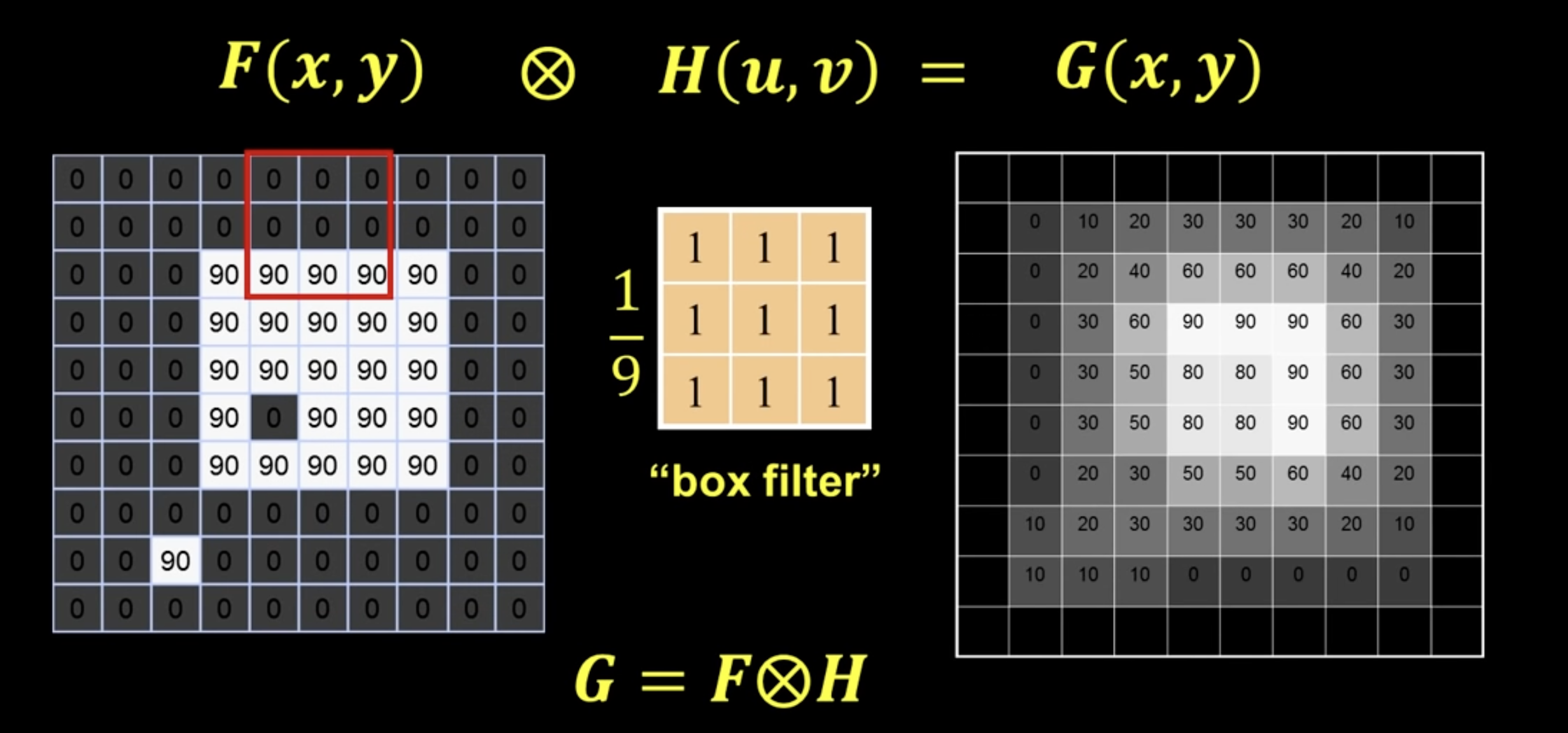
均值平滑后的结果:
效果不好的原因:
如果一个两点失去了焦点,看起来就像是: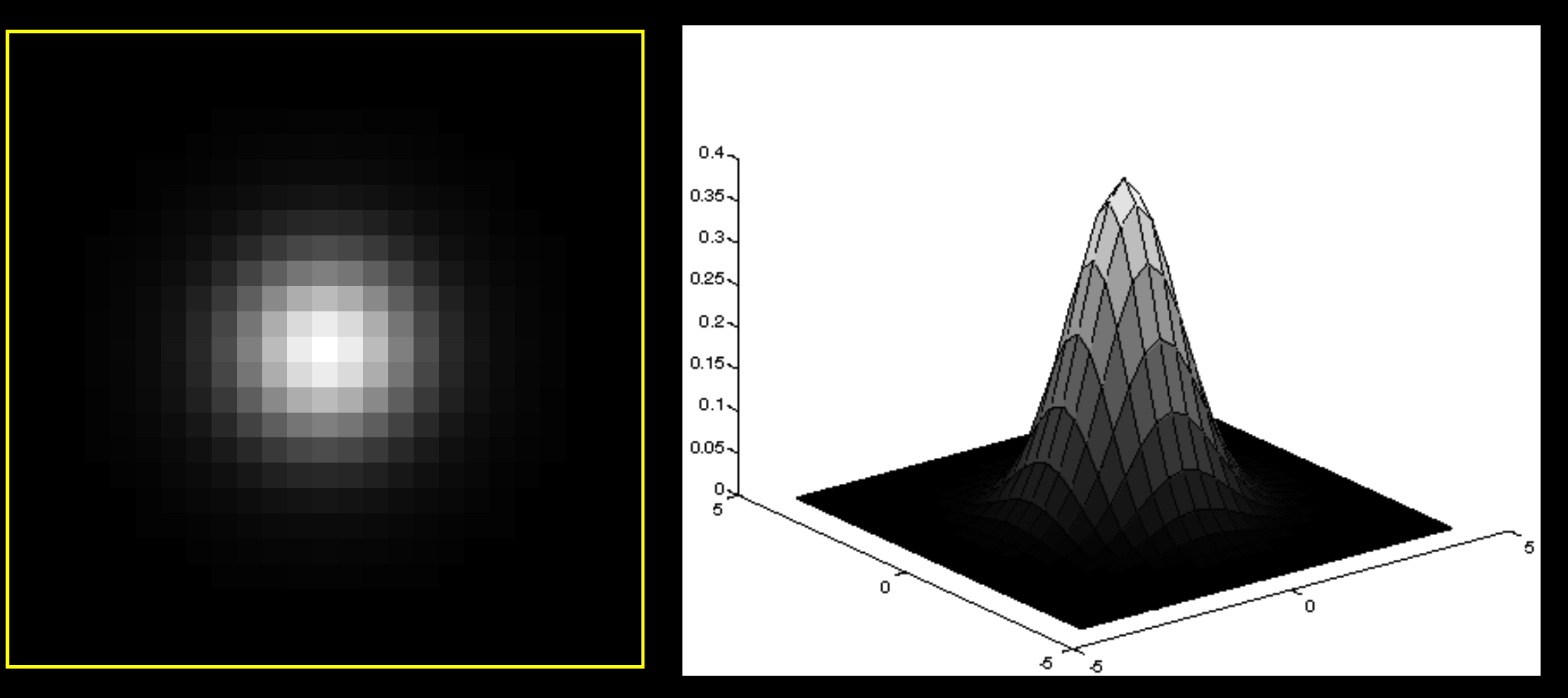
高斯过滤
高斯函数:
高斯过滤后的图像:更加平滑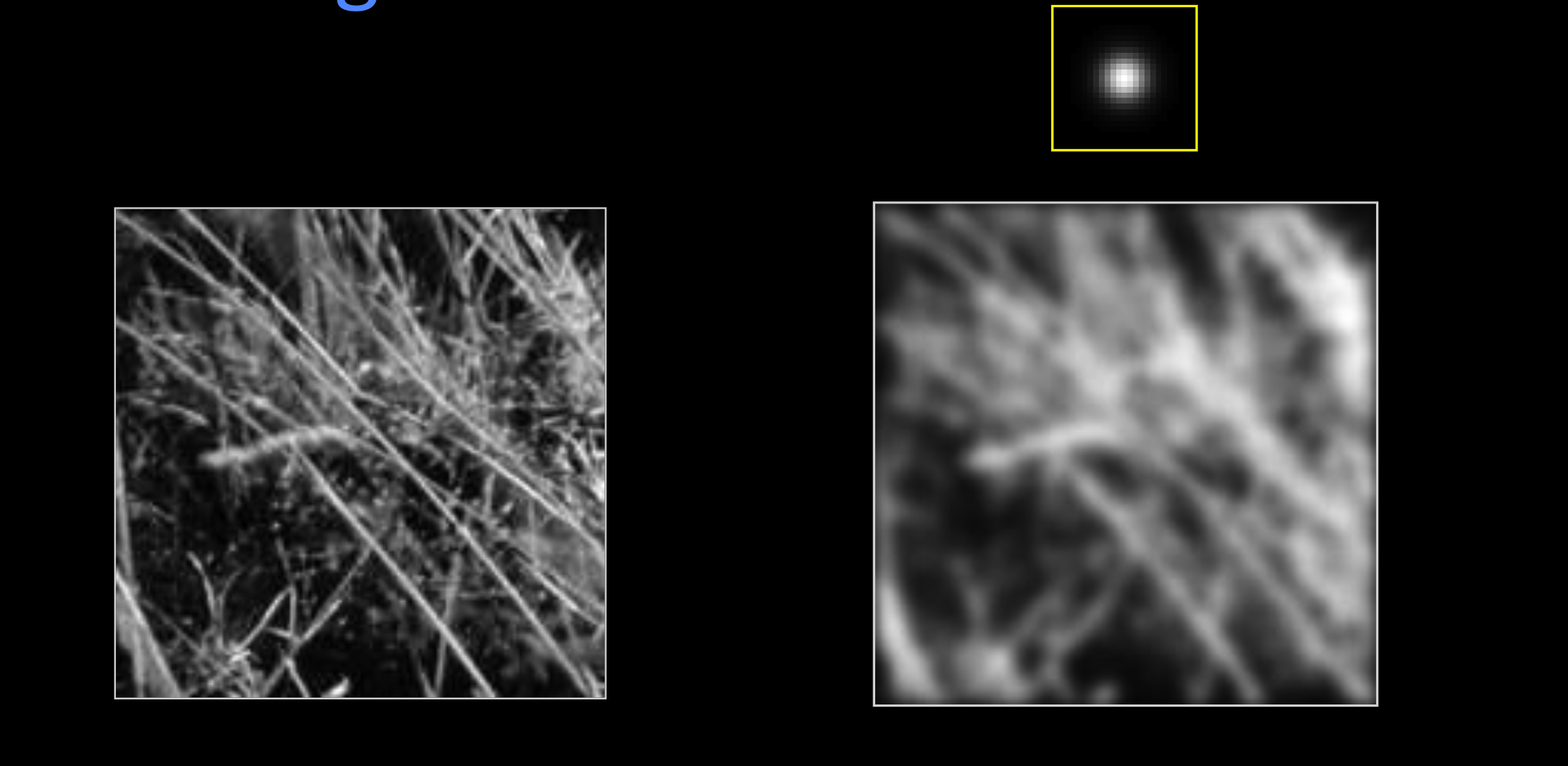
不会出现尖锐的部分
方差与标准差
sigma越大,模糊程度越高, 是高斯的高度,平方是高斯的方差。
关注的有两点,矩阵大小和sigma的值。
高斯过滤:
不同的sigma: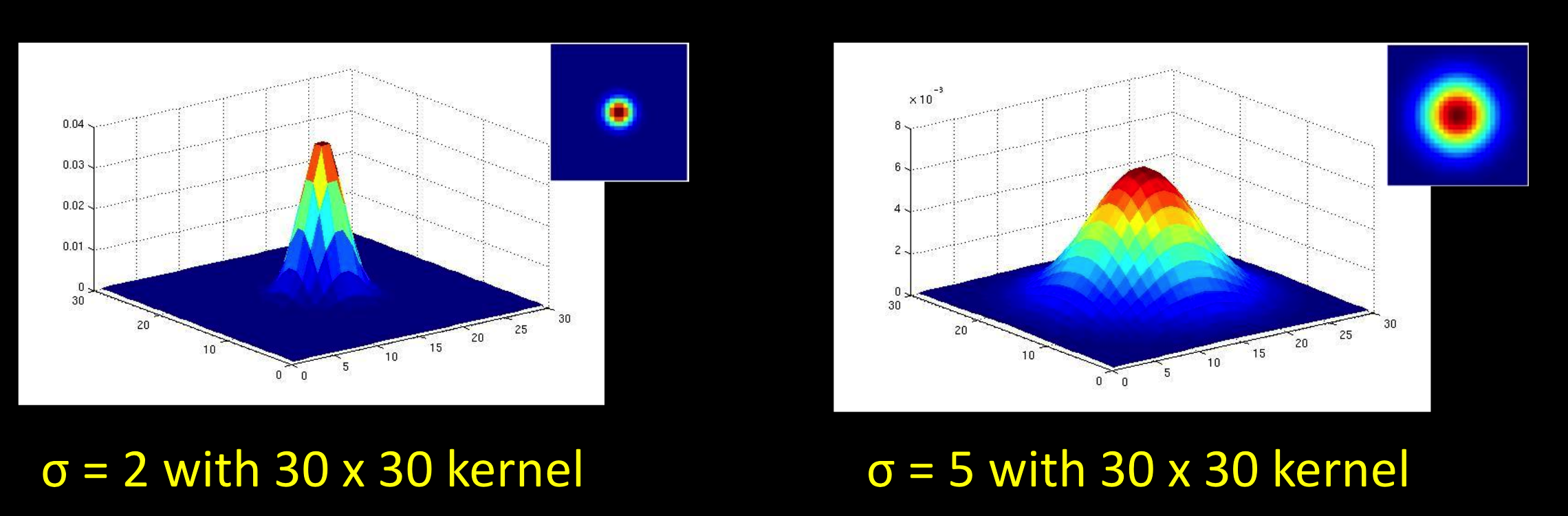
sigma越大,过滤的内容越多。
不同的内核大小: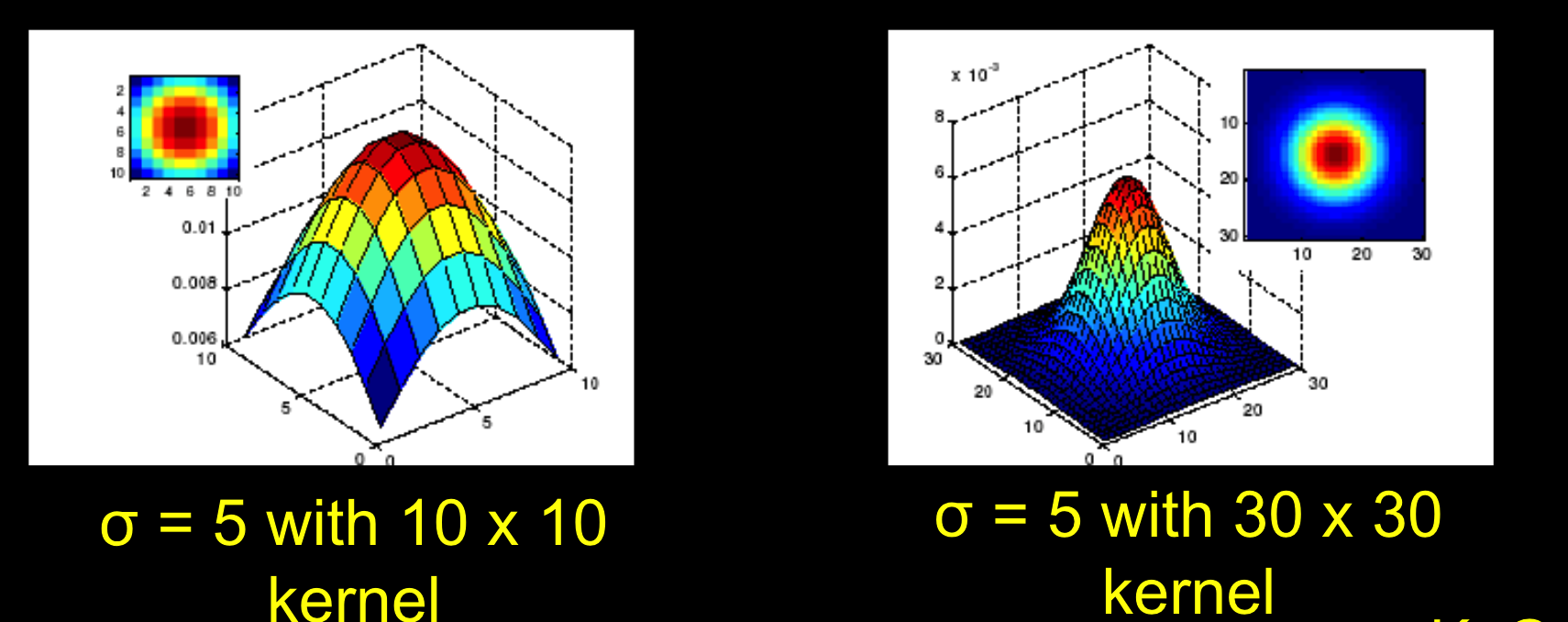
内核更大,平滑效果越好,
两种高斯直线

- sigma越大,噪音越大
- 高斯过滤,相同平滑量的噪声量较小的会更加平滑
两个sigma对应不同阶段的参数
线性算子和卷积
线性变换特点:可加性, 倍乘性
线性算子如何影响整个图像?
脉冲函数: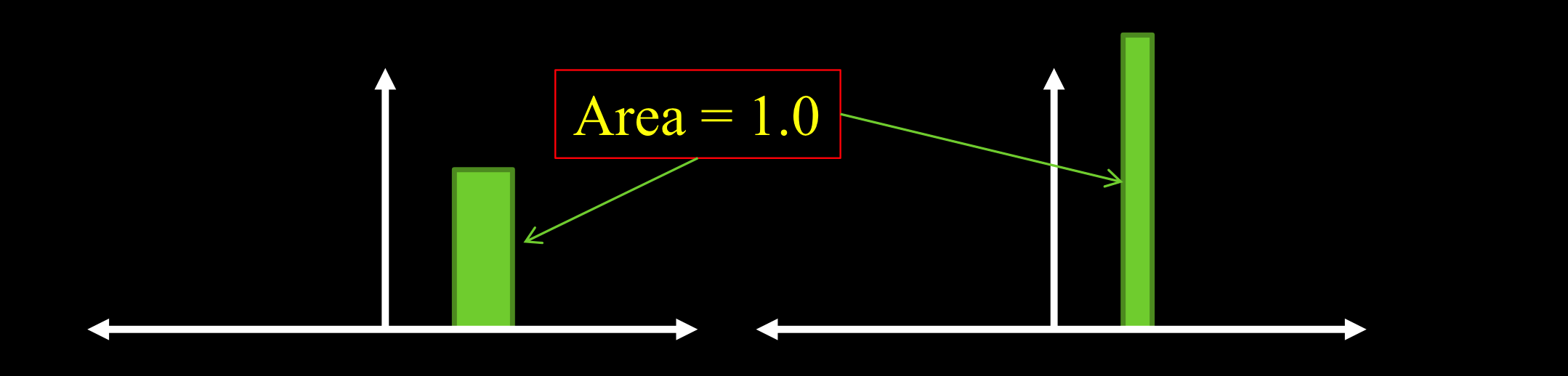
脉冲是一个很小的信号,体积为1。
输入一个脉冲,在黑盒中输出一个响应。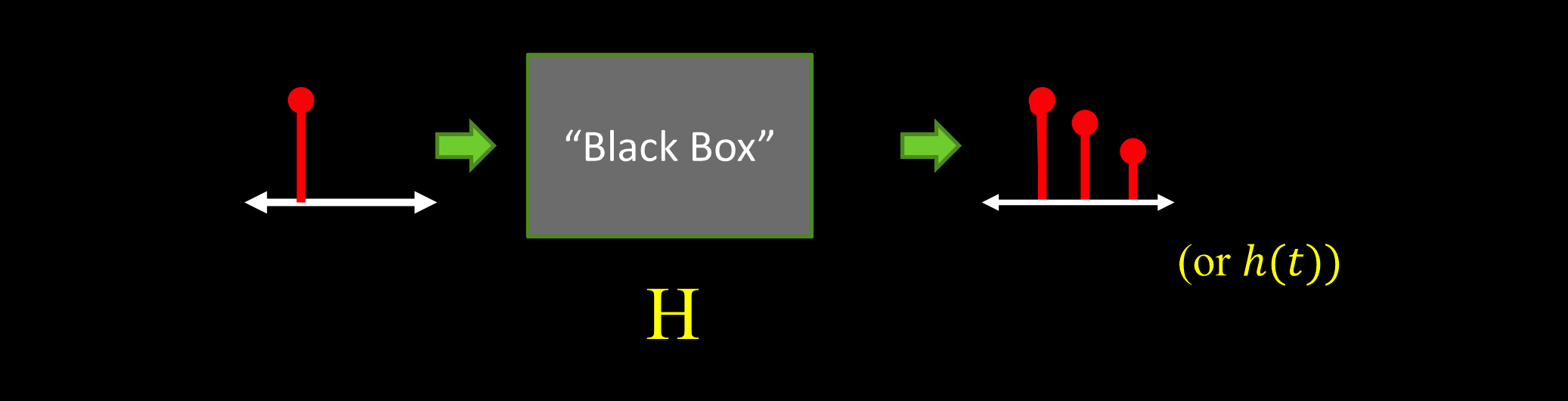
如果知道黑盒如何影响单个脉冲,就可以解释影响整个图像。
过滤脉冲信号
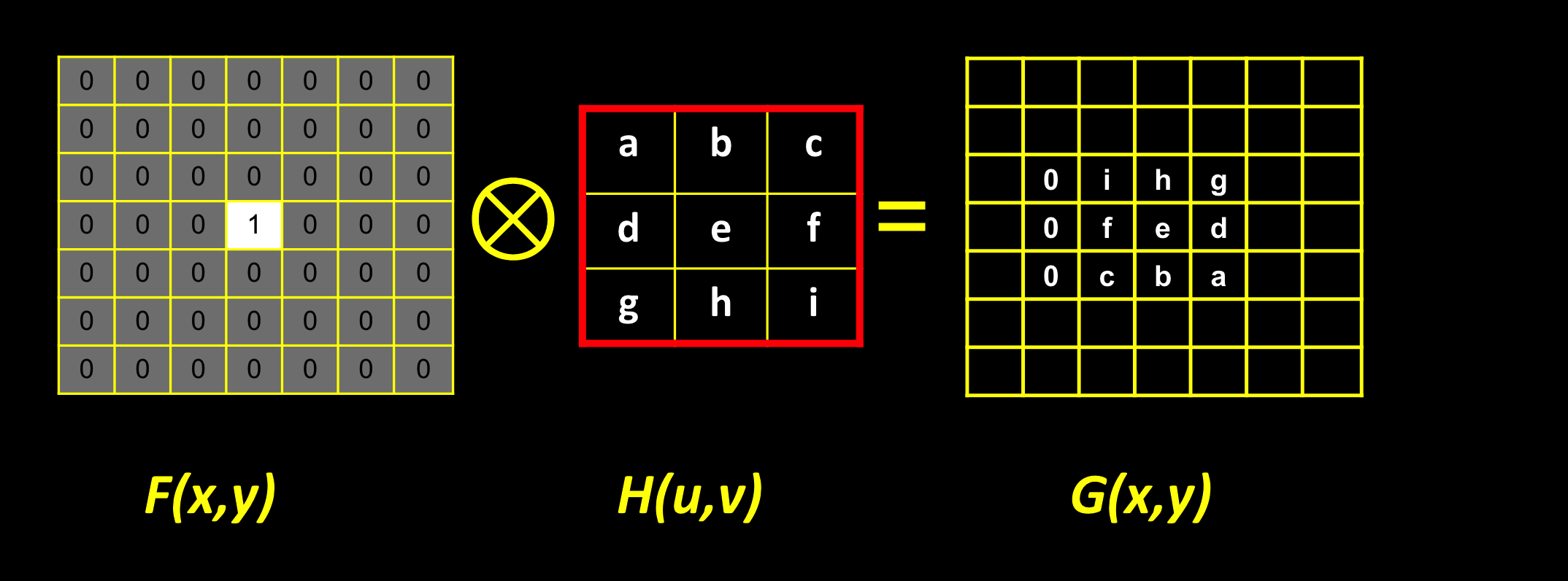
展示了脉冲过滤的翻转情况,假设中心元素为脉冲元素e。
互相关和卷积
互相关
直接应用过滤器:
$G[i, j]=\sum_{u=-k}^k \sum_{v=-k}^k H[u, v] F[i+u, j+v]$
$G=H \otimes F$
卷积
翻转上下,左右:
相当于先把核进行上下左右翻转,然后在应用过滤器:
$G[i, j]=\sum_{u=-k}^k \sum_{v=-k}^k H[u, v] F[i-u, j-v]$
$G=H \star F$
翻转过程为:(*为了方便看到翻转效果)

卷积实际是一种物理学
- 在对称滤波器中,两种操作都是结果都是相同的
- 只有在非对称滤波器中,才能看到区别
卷积的性质
- 线性运算
- 结合律
- 交换律
- 单位脉冲和整个脉冲操作相同
- 微分性质
卷积的导数等于第一个元素的导数与第二个元素的卷积
$\frac\partial{\partial x}(f*g)=\frac{\partial f}{\partial x}*g$
边缘检测和梯度查找会用到
计算的复杂性和可分离性
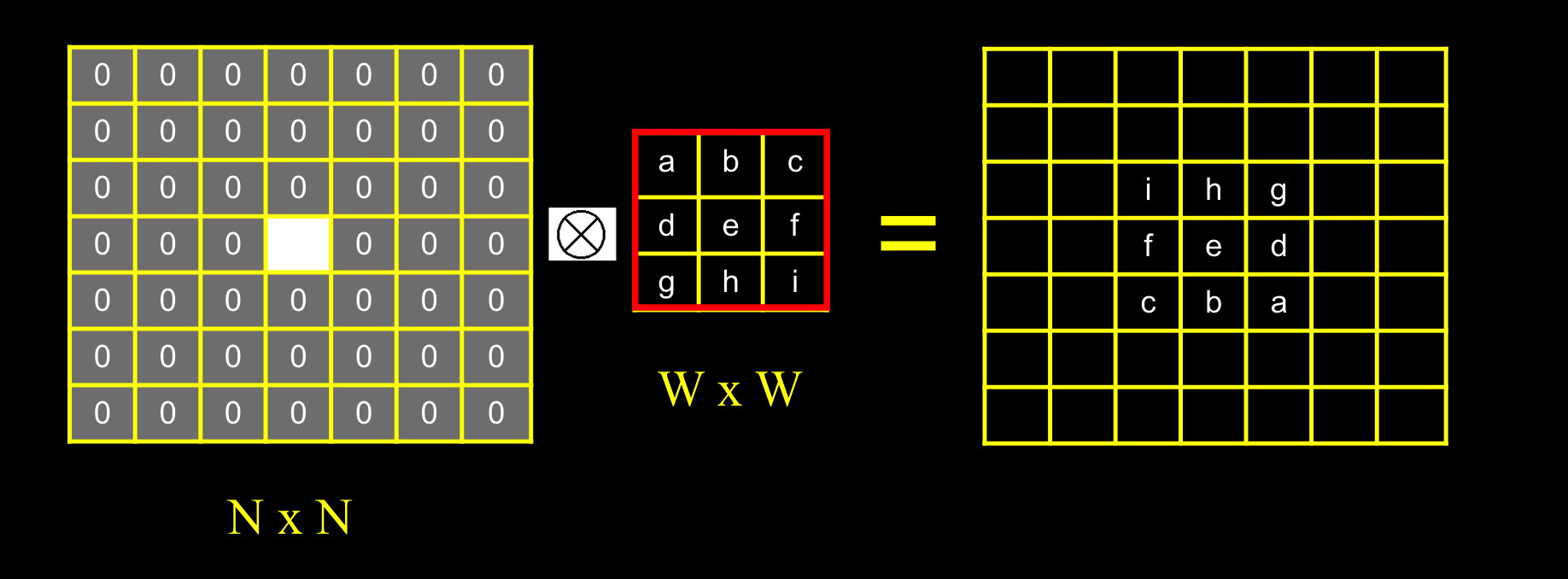
乘法的操作次数需要:$NNW*W$
线性可分离核: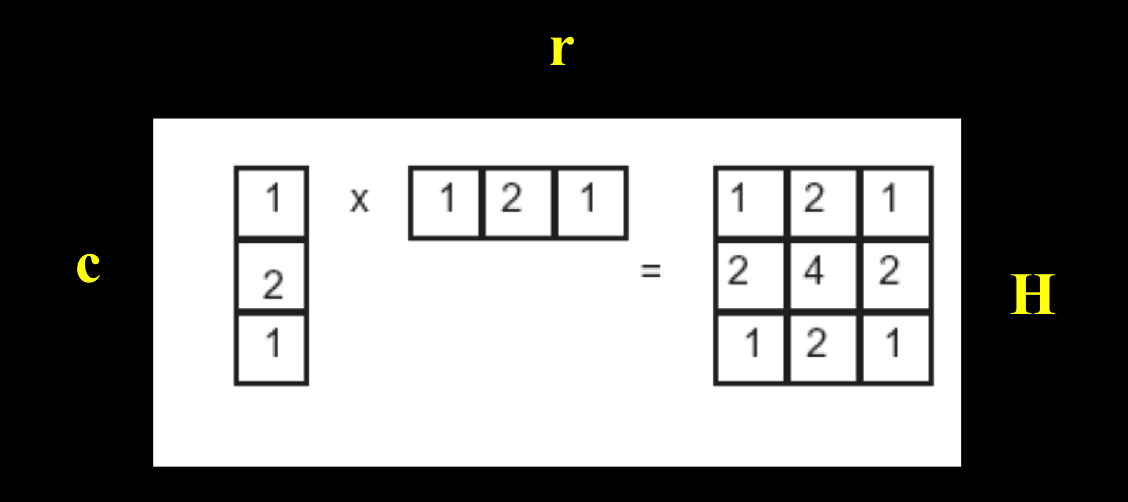
假设其他位置元素为0,结果为一列向量乘行向量。
可分离卷积操作:
$G=H*F=(C*R)*F=C*(R*F)$
乘法操作次数为:$2{\cdot}W{\cdot}N^2<<W^2{\cdot}N^2$
边界问题
过滤器会不会从边界掉下去?
一共有三种边界处理方式: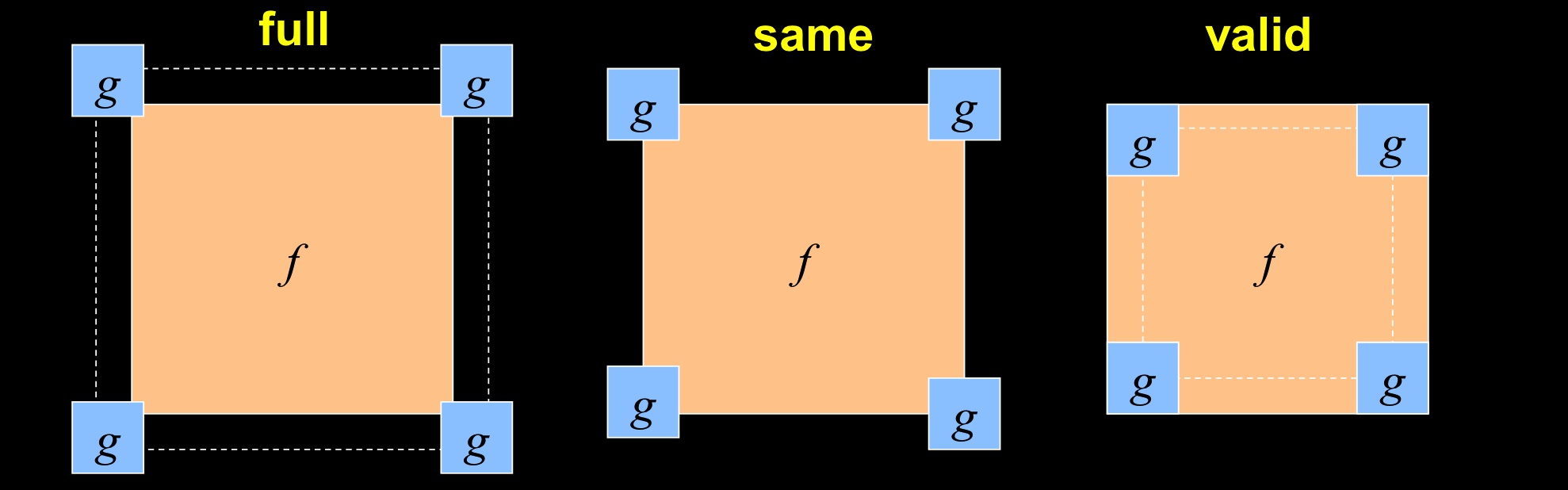
具体的方法:
剪辑-clip filter
假设边缘是黑的,结果会让边缘变暗,因为黑色渗入了
环绕法-wrap around
与傅里叶分析有关
假设图片一周围绕的像素与图像边缘有关:右边填充为左边的图像,上边填充为下边的图像
过滤效果:

图像的上边缘会泛红,来源于下边
类似一种周期性信号,但是在图像过滤中效果不好
边缘复制法-copy edge
填充复制图像边缘
效果: 图像基本保持不变,是一个合理的结果

反射法-reflect across edge
填充的是边缘的反射
效果也是很好:

联联系线性滤波器
用脉冲对图像过滤,得到的还是原图像: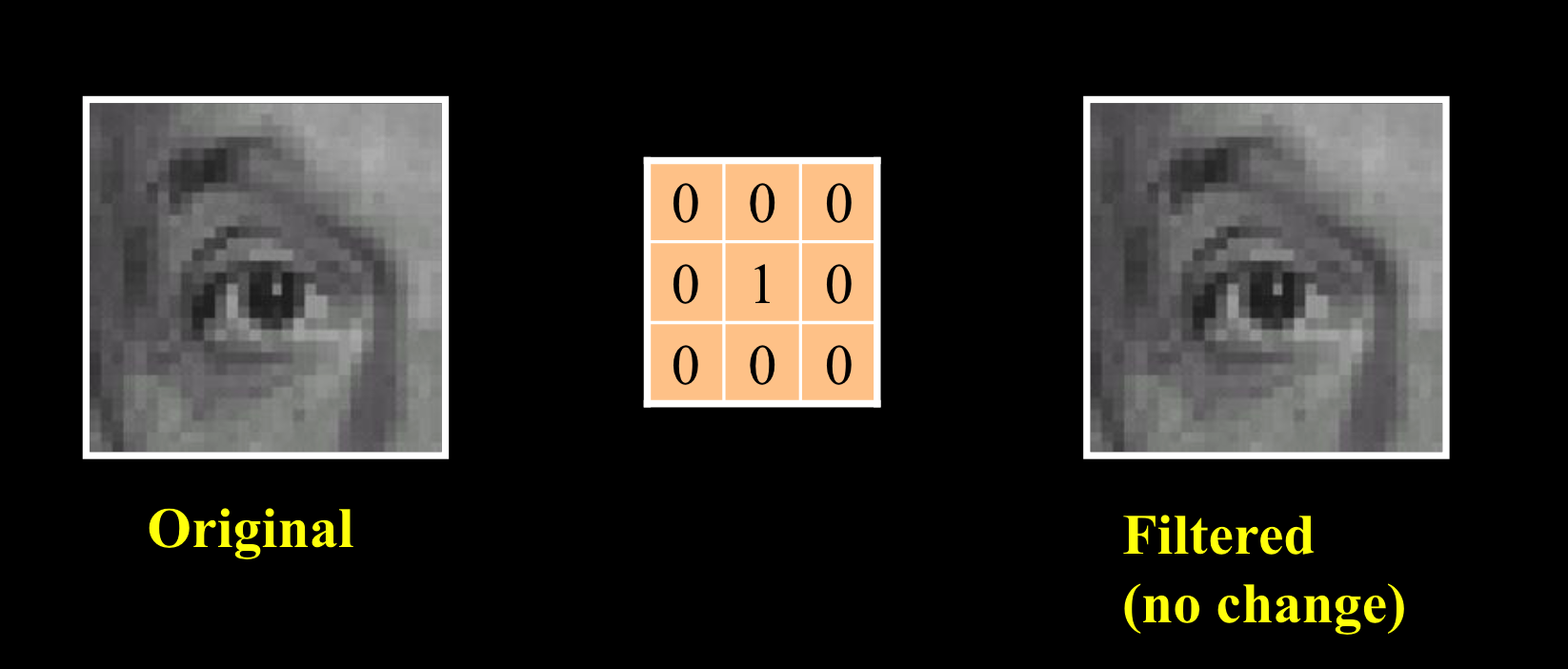
使用向右移动了一位的脉冲,过滤结果:图中进行的是相关操作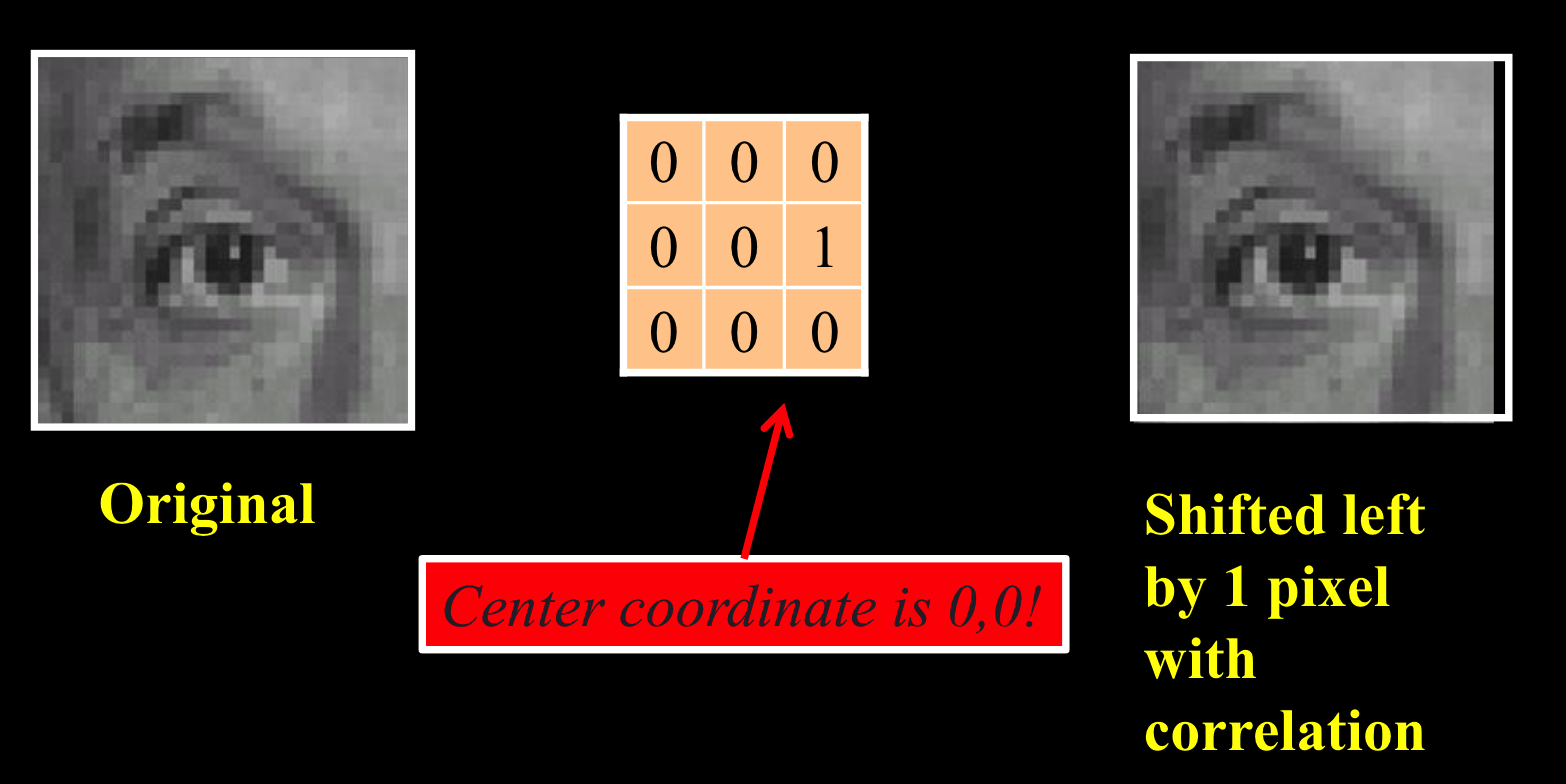
取向左还是向右,取决于做相关还是卷积操作:
模糊的平滑滤镜: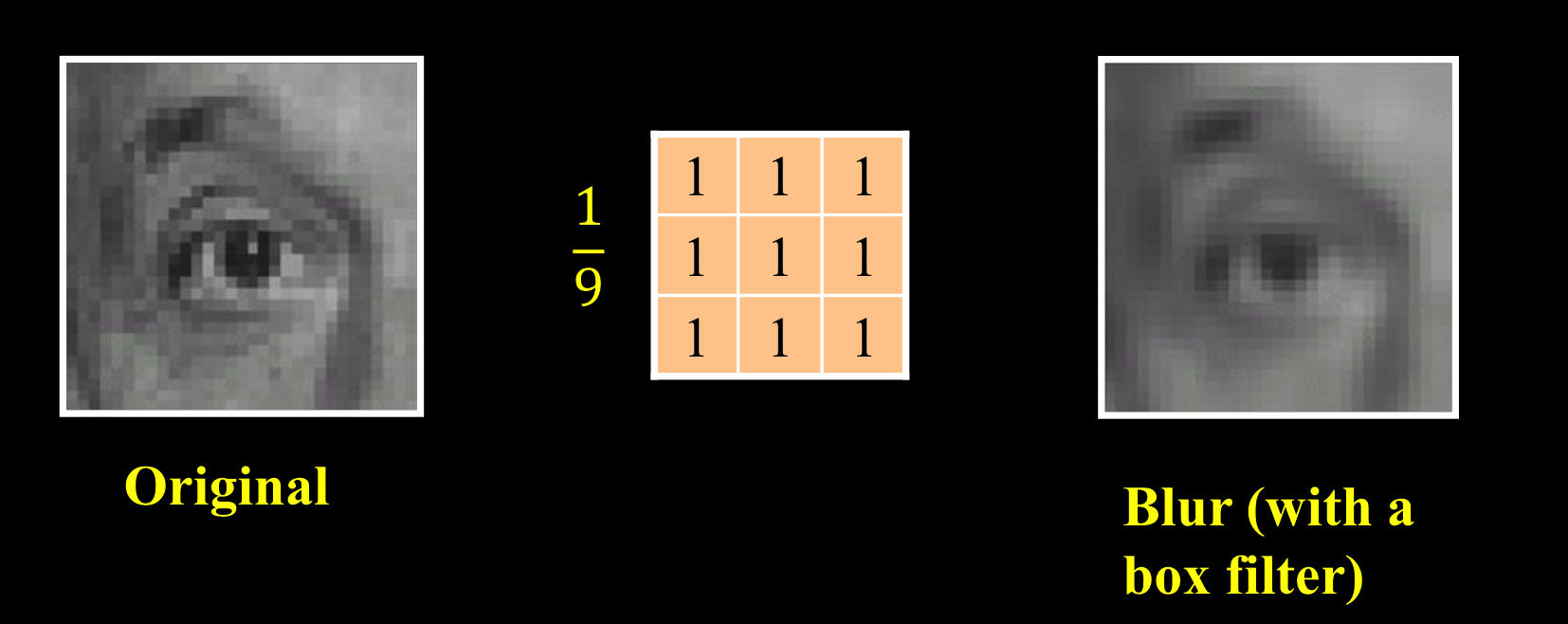
特殊的过滤器:(脉冲的两倍,减去模糊)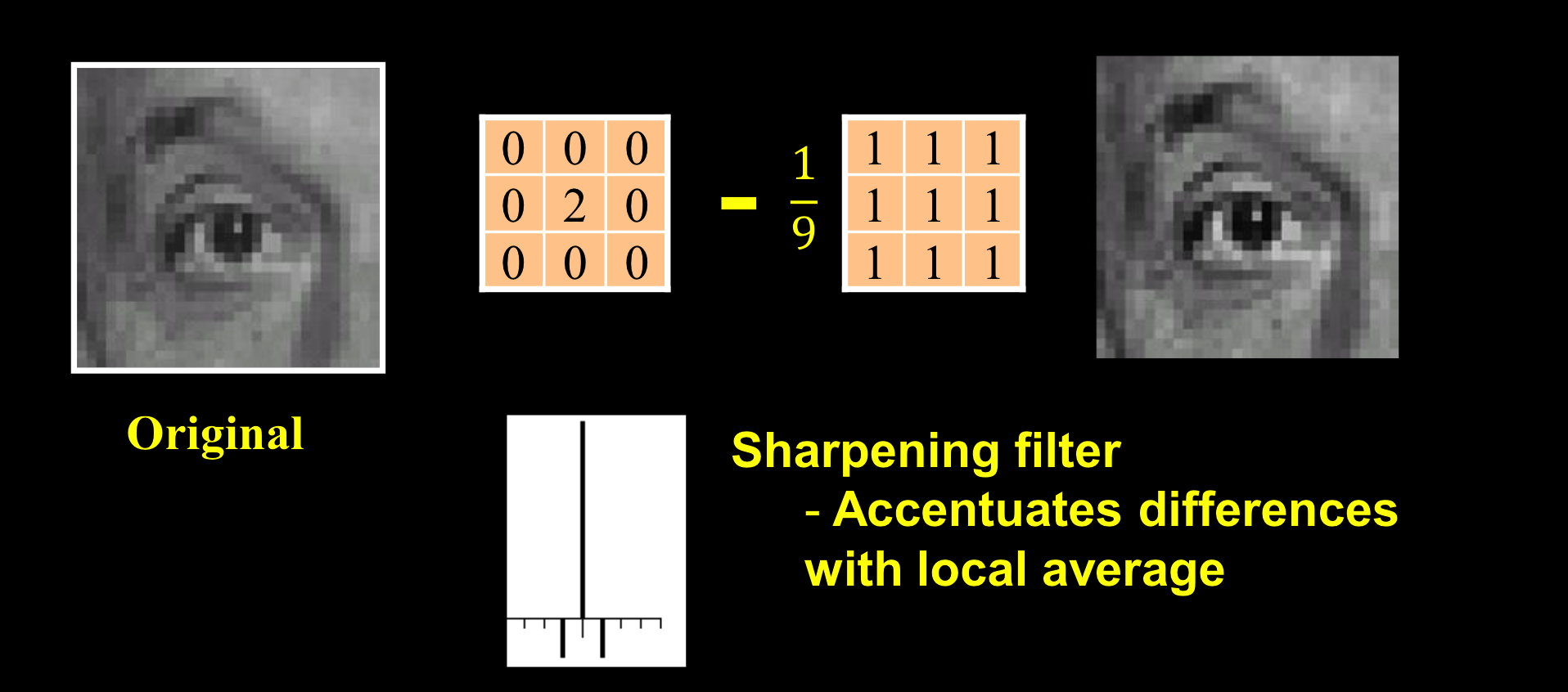
锐化图像,强调差异
应用:

非锐化滤镜:(unsharp mask)
类似冲洗胶片,将白光照射,得到底片的负片。
对应上图的锐化:底片的负片减去模糊的部分,得到的是更清晰的图片。
模糊的部分是不清晰的蒙版,加入图像后得到了更清晰的图像。
其他类型的噪音与对应的非线性过滤器
高斯噪音与椒盐噪音
过滤的本质是从周围的像素点找一个局部平均值替换。
当噪音趋于0时,可以很好的过滤噪音,如果把完全随机的值加入图像,就需要其他过滤方法,比如中值过滤器。
中值过滤器:(median filter)
将中间的白色像素90,替换为中值,非线性的,不可以复原.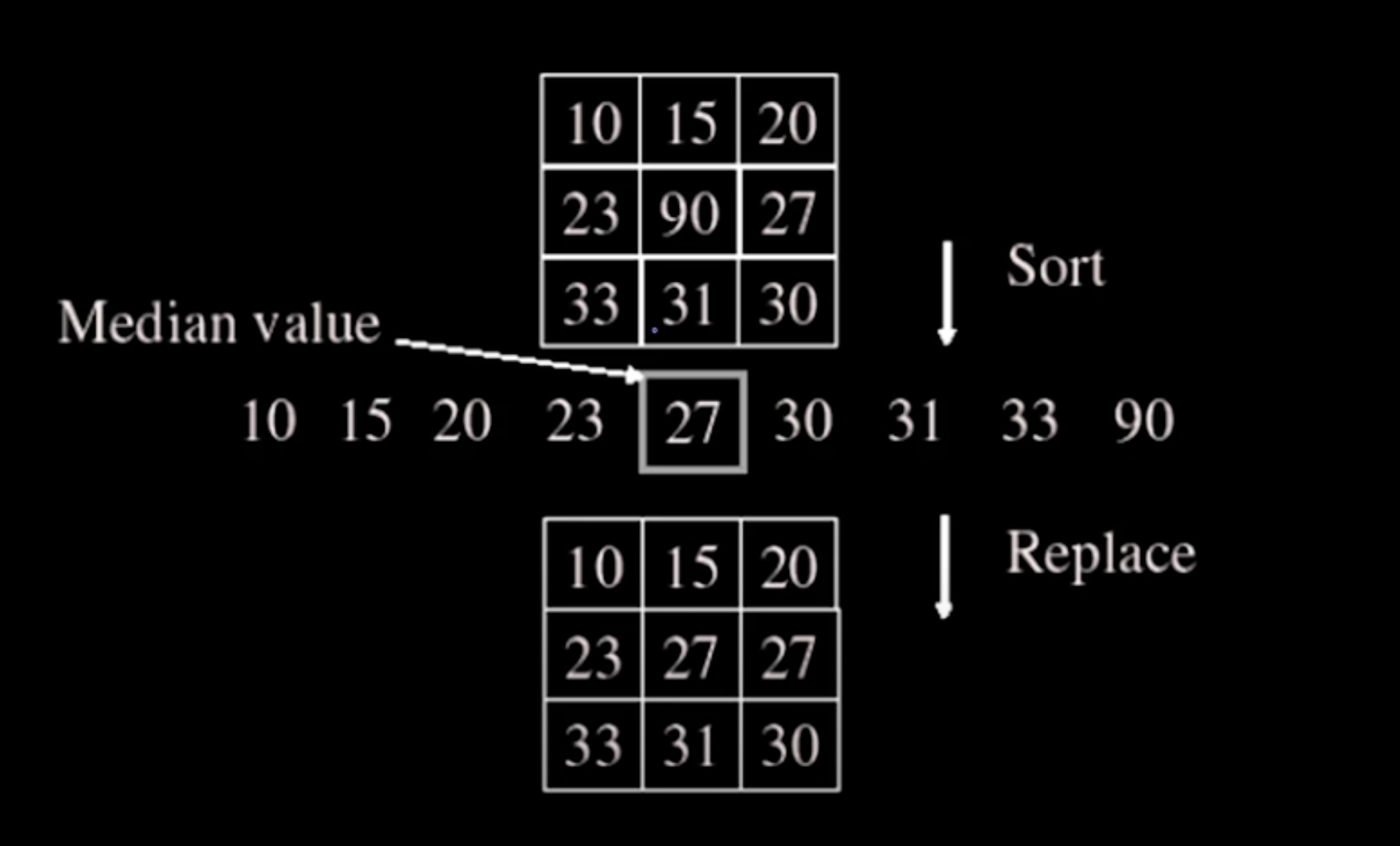
对椒盐噪音效果很好: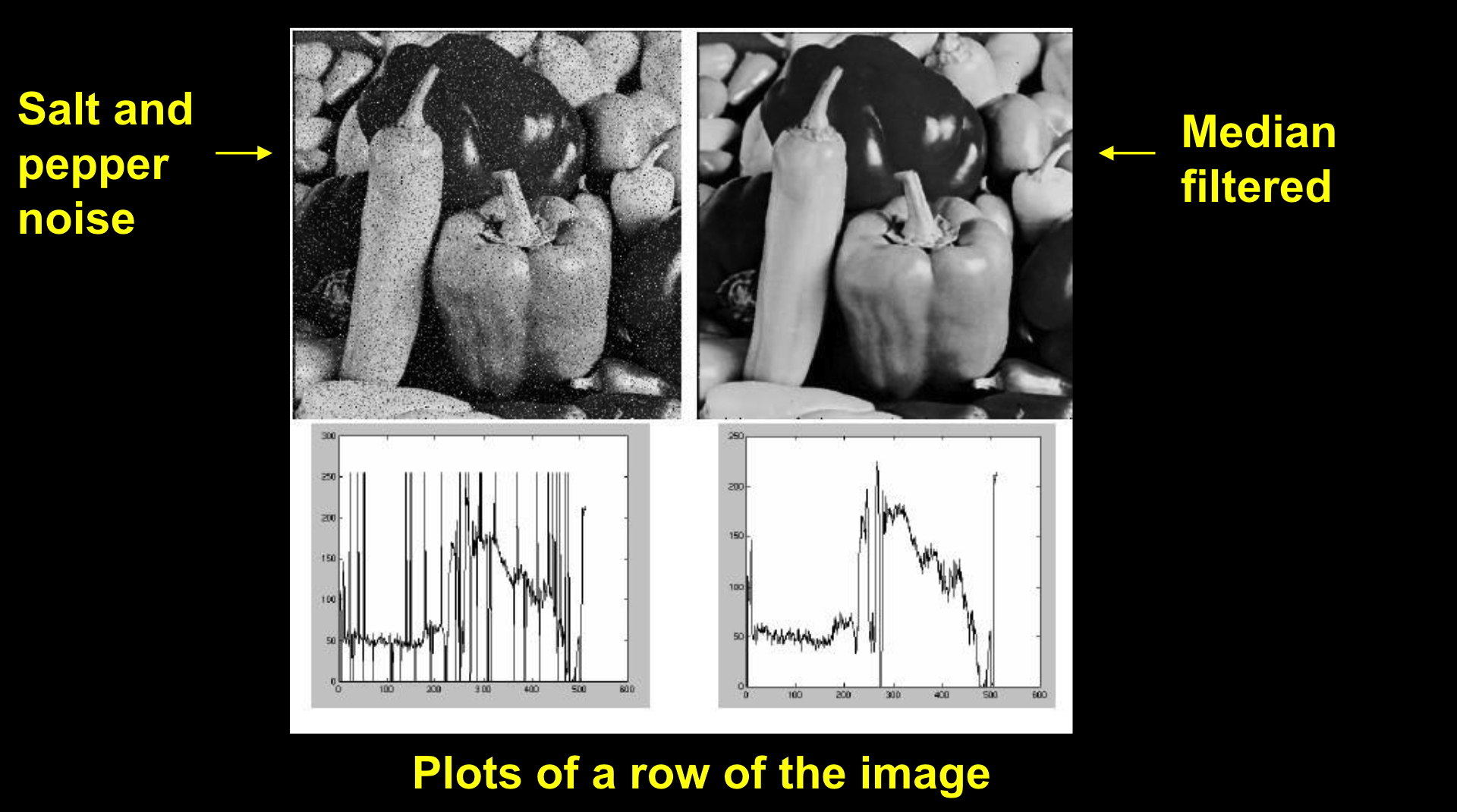
非线性的过滤: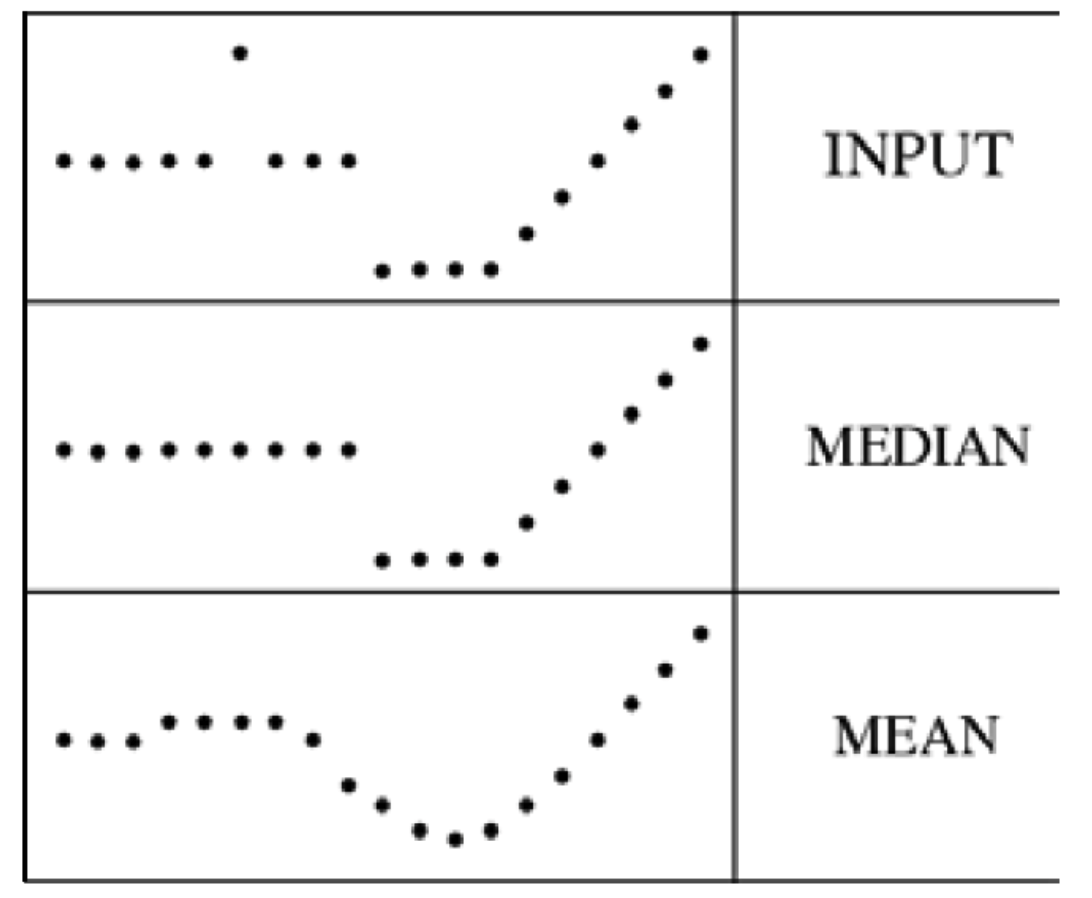
有时也称为边缘保留
相对于均值过滤,它保留了图像像素边缘非平滑。
过滤用作模式匹配
归一化相关性
两件事:1. 对过滤器进行标准化。2.用过滤器将box内的像素变为标准差为1。
1D 信号
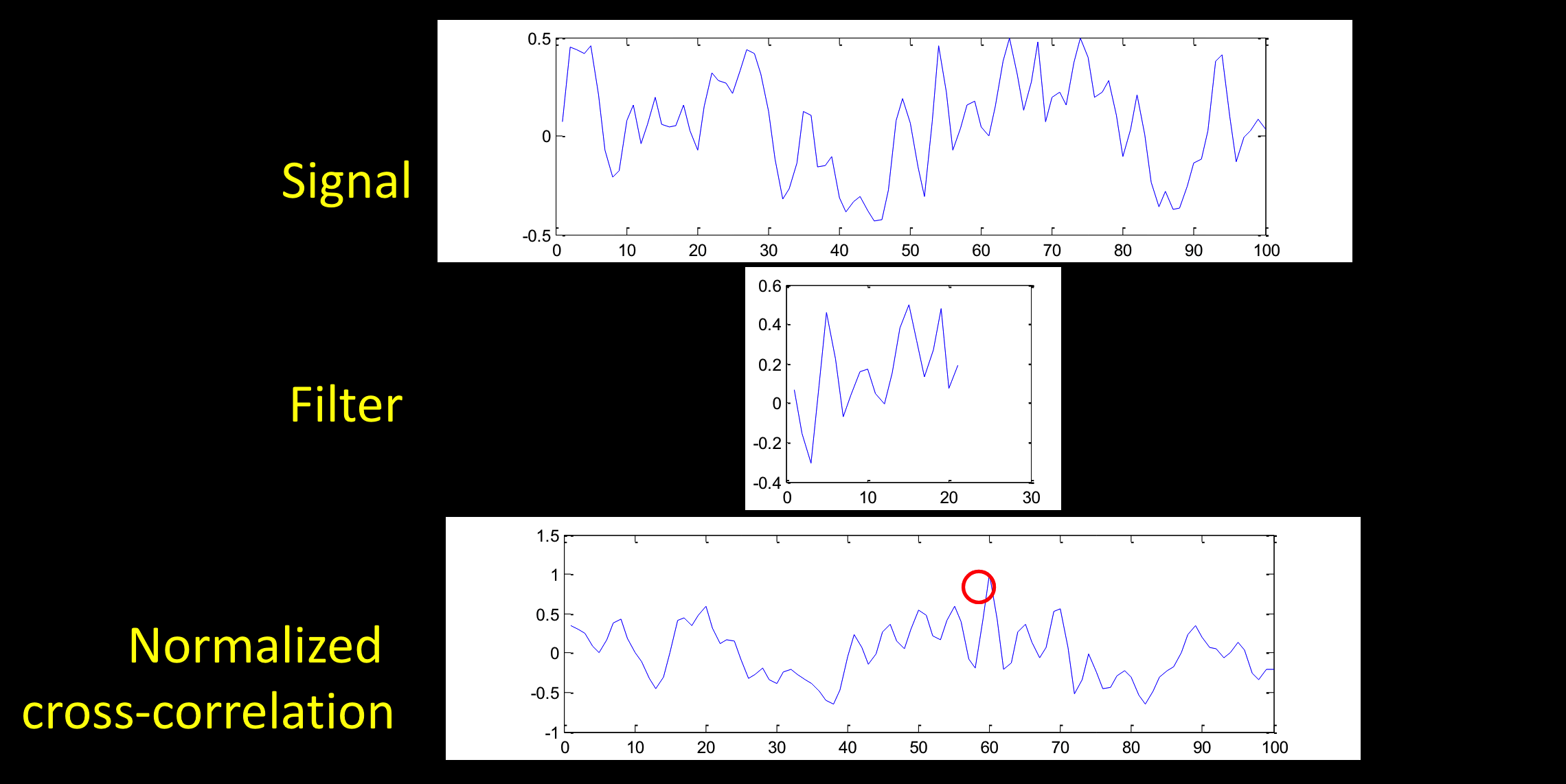
用所示的滤波器,对信号进行归一化相关:
滤波器来源于信号的某一段,在此处,归一化相关后得到峰值。
原理,在归一化处理后的正负图像中,乘一个自己相同的滤波器,得到的值最大,负负为正。峰值处:正值与正值对齐,负值与负值对齐。
对应于图像: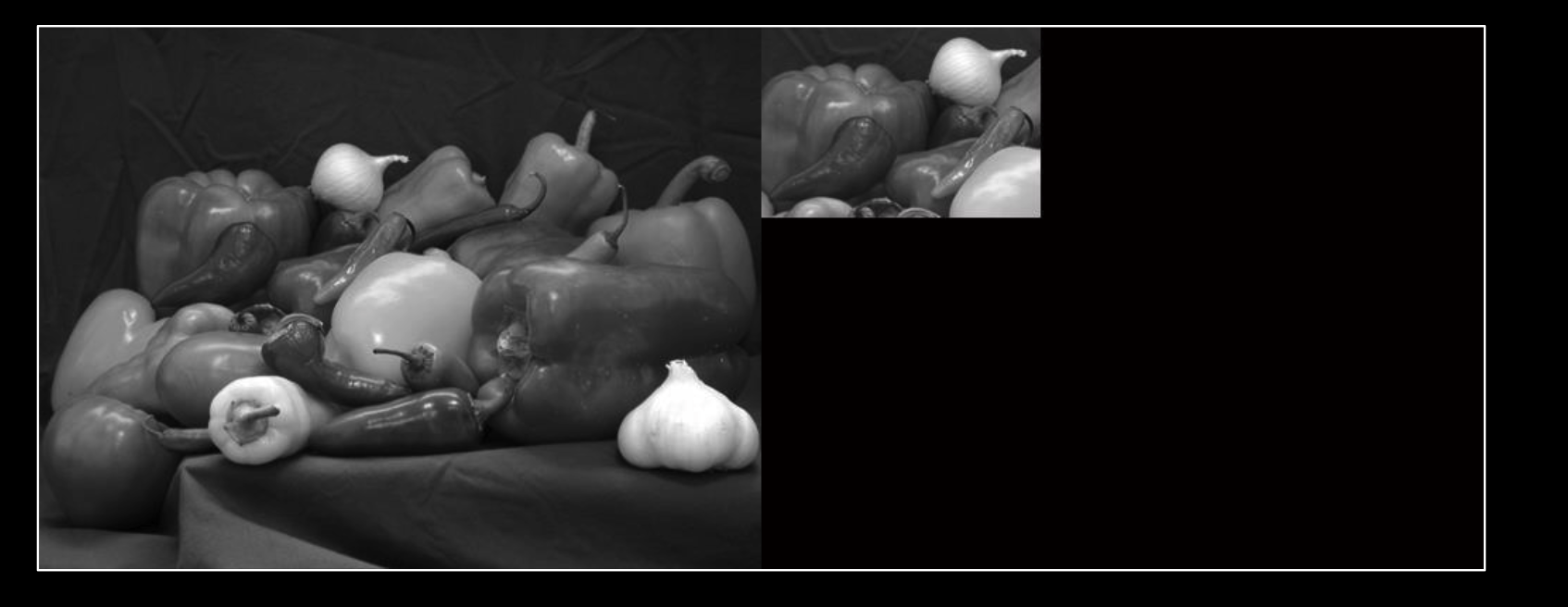
相关后的图像函数图,在相似位置的值为峰值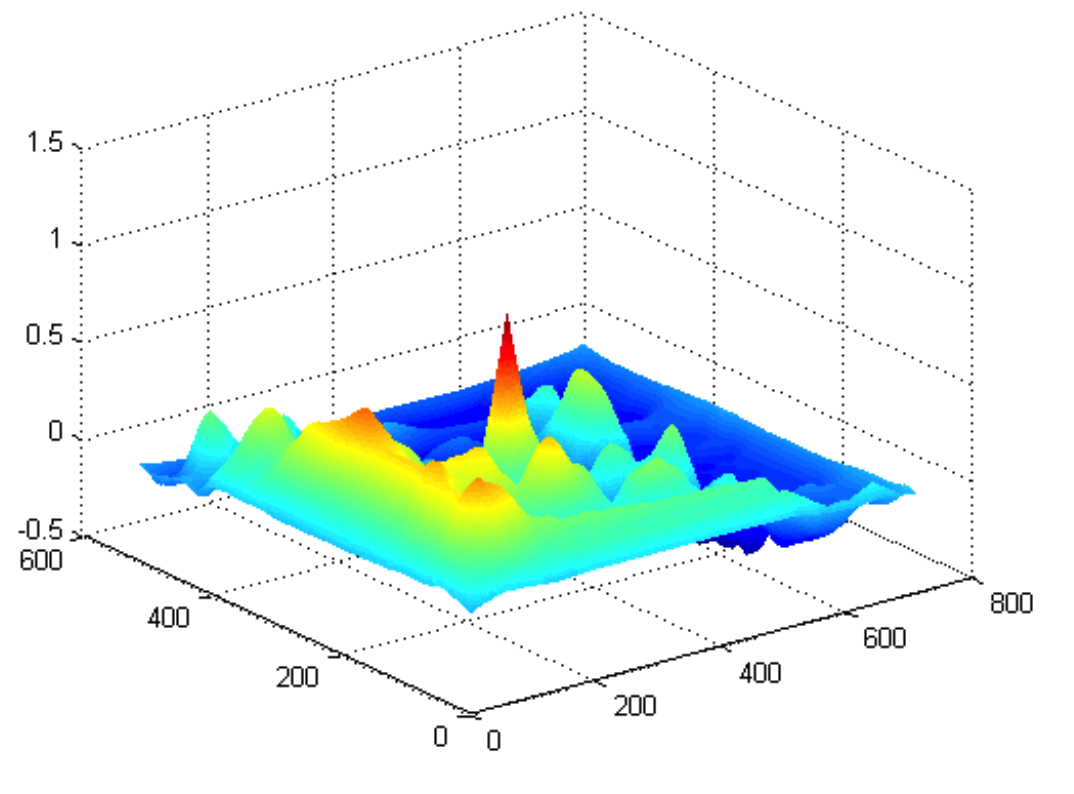
解释了过滤器如何用作模式匹配。
模式识别
简单的例子: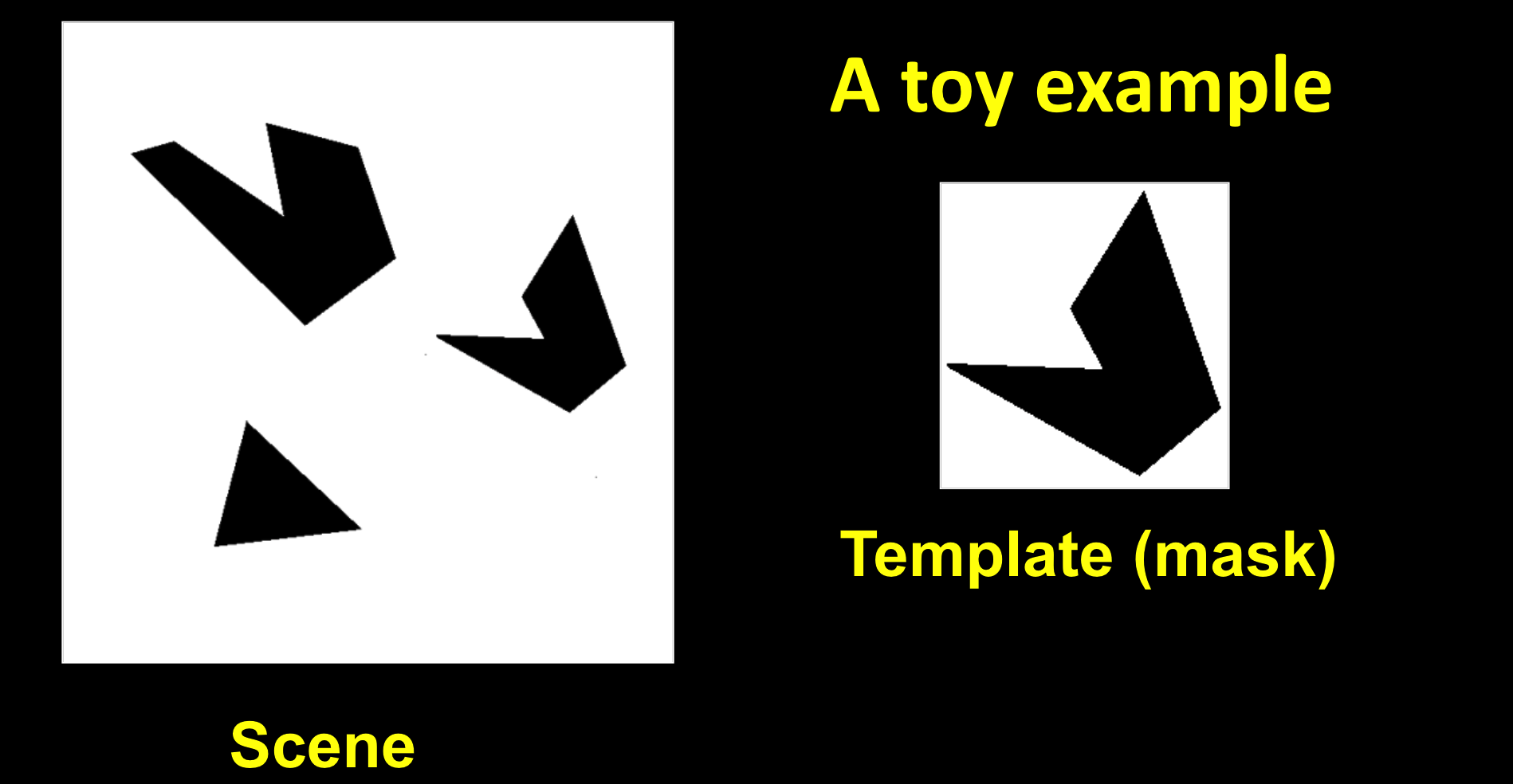
使用相关性进行检测:
最亮的点就是检测到的位置。
沃尔多在哪里?

相同的结果:找到最亮的点。
图像不同的情况:

匹配错误。
边缘检测:梯度
如果事先不知道要找的图像模板,如何在图像中找到有用的信息,图像的特征。
简化图像:
图中的所有信息大多来源于边缘。
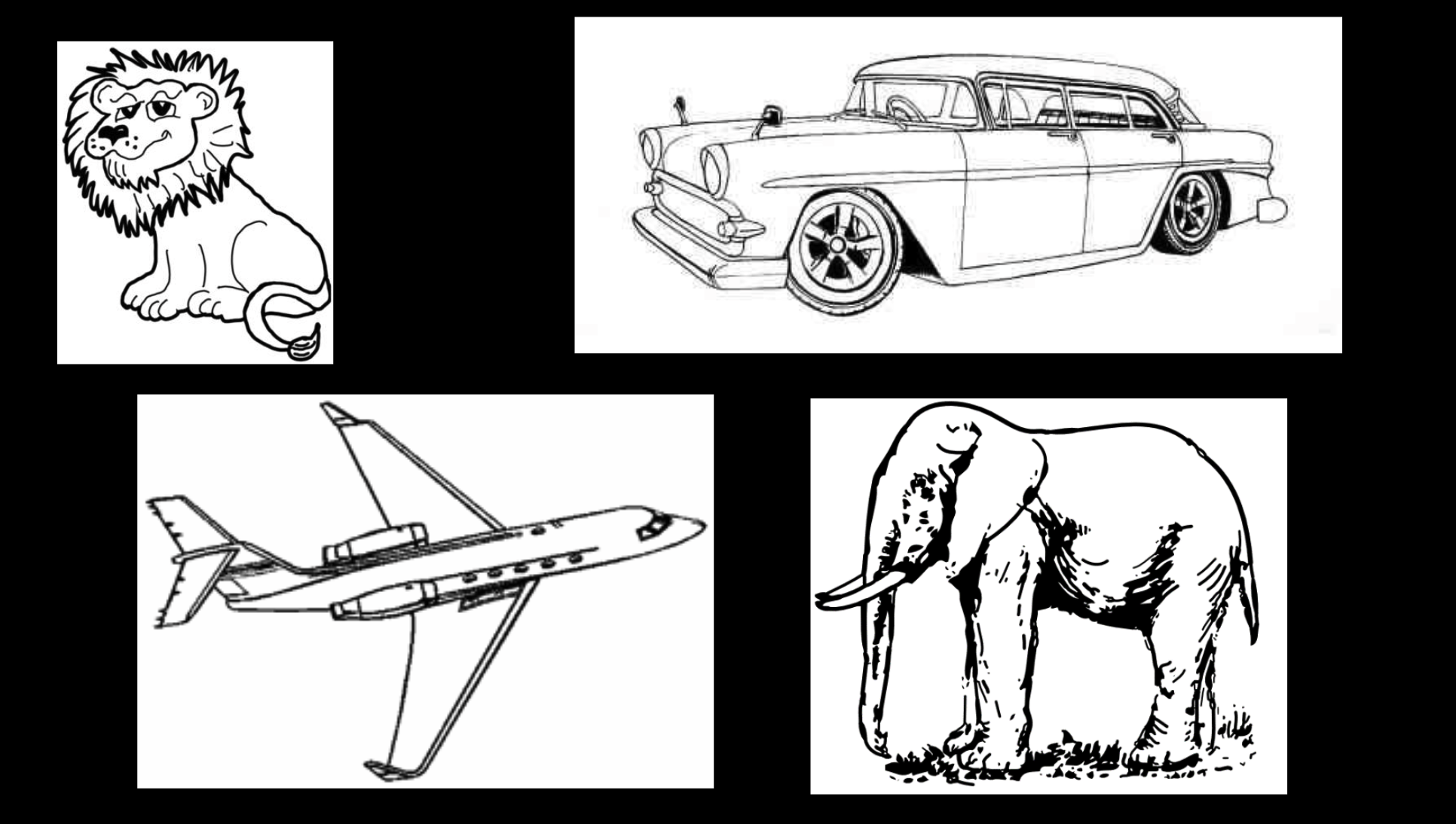
边缘:
上图中分别有深度边缘,阴影边缘,颜色的边缘,形状的边缘。

图中包含了纹理边缘。
边缘检测:
找出图像函数的边缘像素: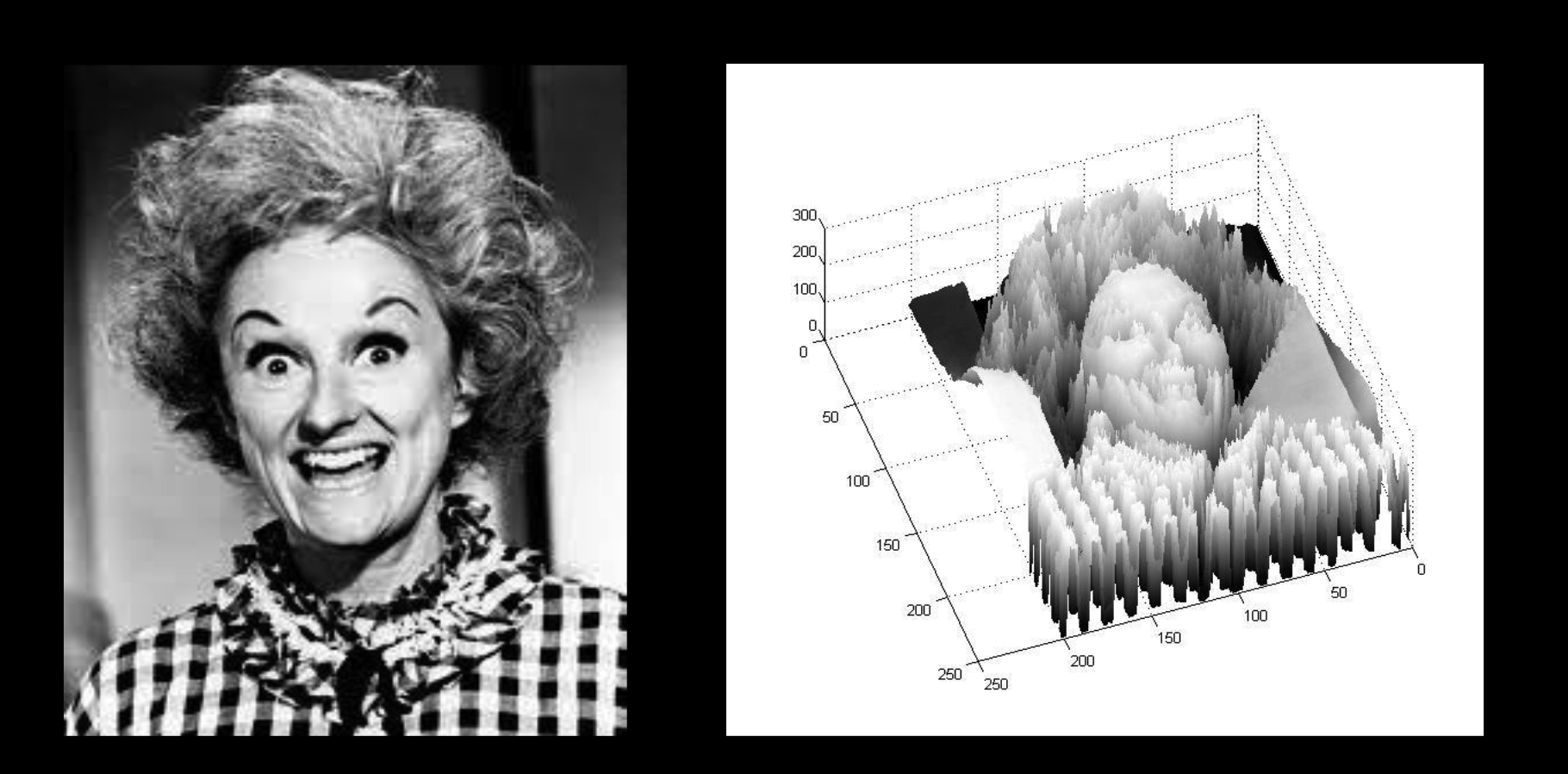
从高度函数中可以看到,急剧变化的位置就是边缘像素。
边缘检测的问题:
- 边缘有多大
- 变化的范围是多少
导数和边缘
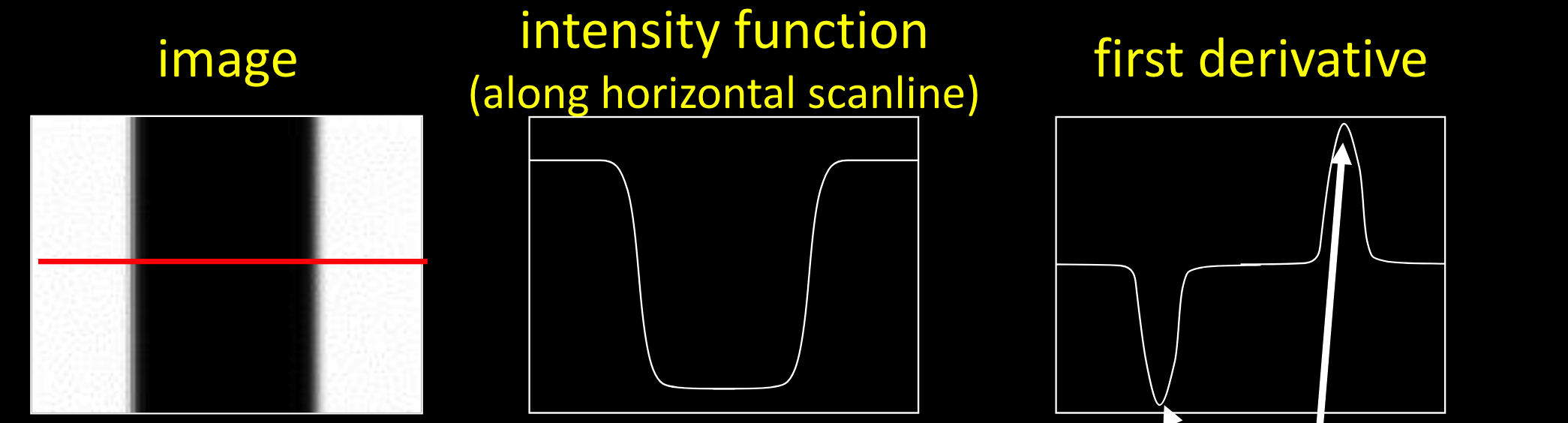
右图中的一阶导数函数图,极值点对应的就是图像边缘像素。
什么是梯度

梯度是:图像变化最快的方向。大小是单位长度上变化的强度。
图像的梯度:$\nabla f = [\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}]$
梯度的方向:$\theta^2=\tan^{-1}(\frac{\partial f}{\partial y}/\frac{\partial f}{\partial x})$
边缘变化的强度:$\left\|\nabla f\right\|=\sqrt{(\frac{\partial f}{\partial x})^2+(\frac{\partial f}{\partial y})^2}$
幅度检测:
离散梯度:(在离散数中,极限无法靠近,只能使用有限差分)
定义为:
\begin{split}
\frac{\partial f\left(x,y\right)}{\partial x}&\approx\frac{f\left(x+1,y\right)-f\left(x,y\right)}1\\&\approx f\left(x+1,y\right)-f\left(x,y\right)
\end{split}
梯度是对$x$,还是$y$做偏导?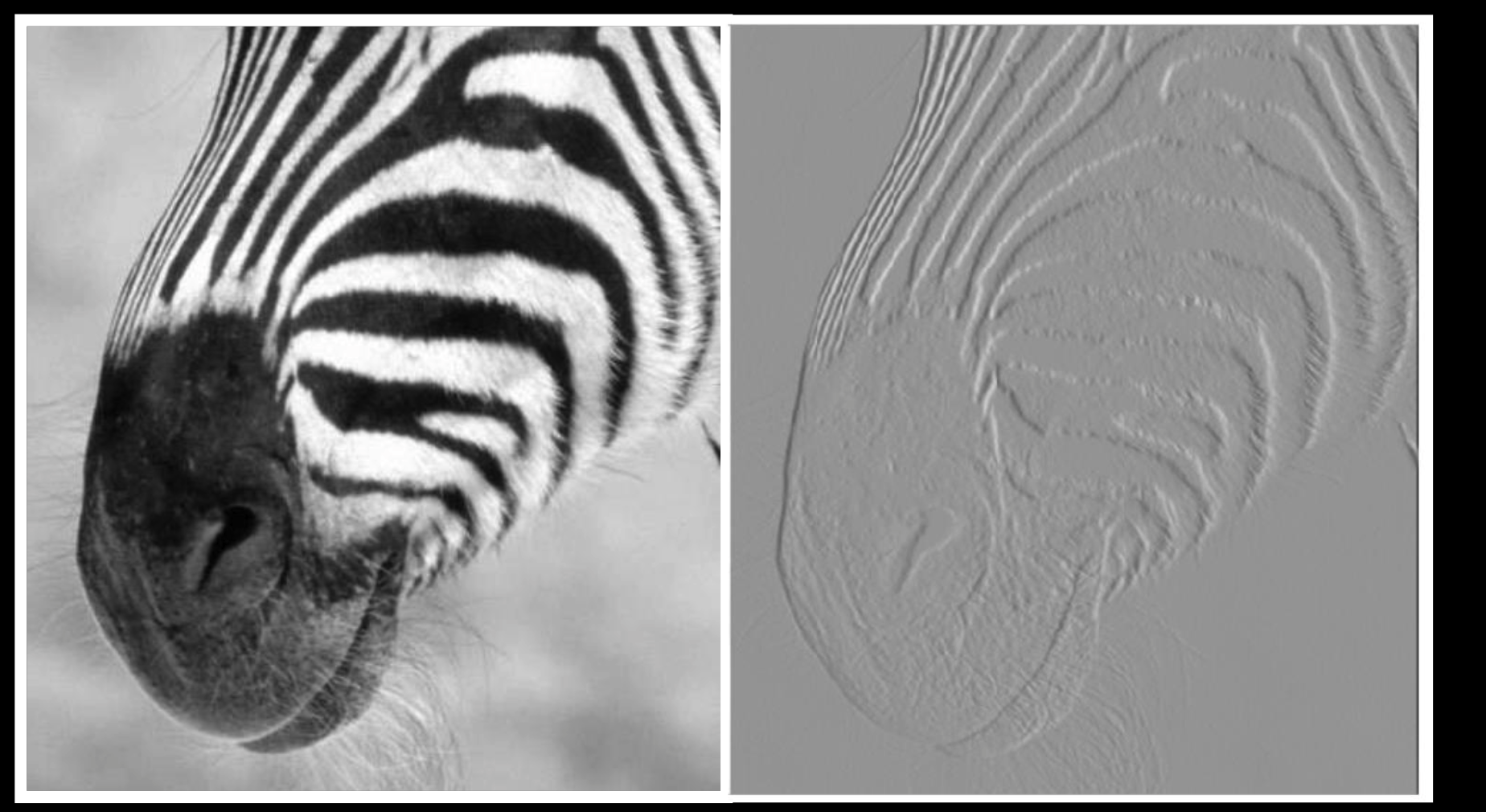
上图中可以看出,在垂直方向对x的梯度可以求出边缘像素,但是在水平方向的边缘像素效果不好。上图是一个对x的有限差分
上图也是一个正负图,负数为黑色,正数为白色,零是灰色。
图像的偏导数
很容易可以看出:左边是对x的偏导图,右边是对y的偏导图。
使用的相关过滤器:
- 对x:将右边的像素减去左边的像素,增强对比。
- 对y:有两种,取决于想让y上升还是下降
离散梯度:使用运算符$H$实现
由公式可以得出,梯度为左边的像素减去自己的像素。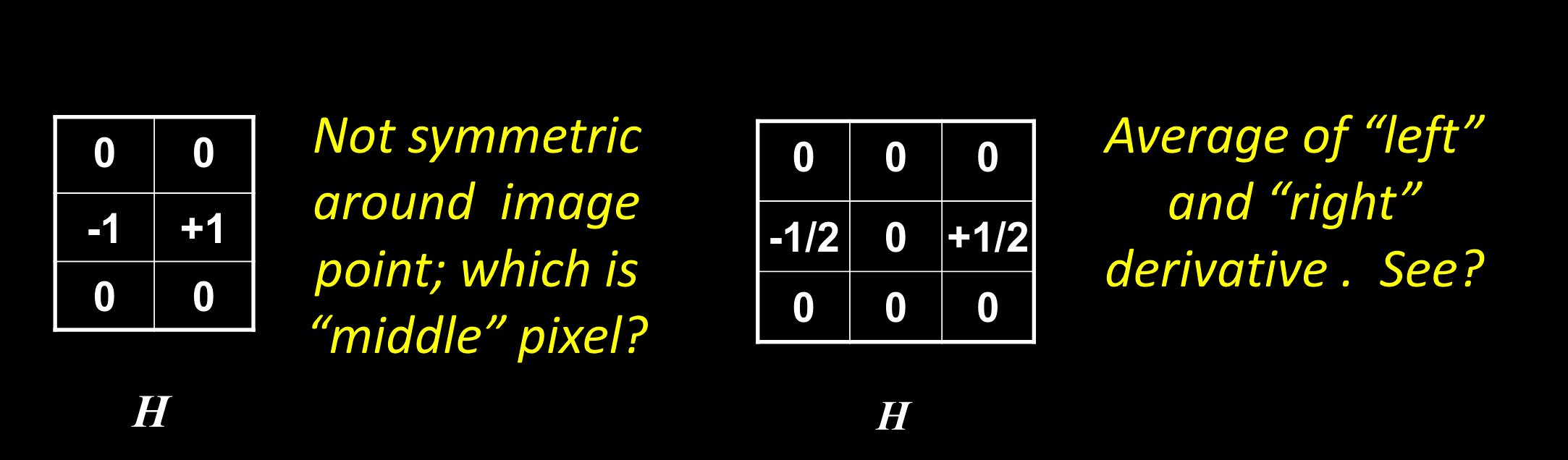
- 第一种运算符:没有中间元素,且只输出了右边的梯度
- 第二种运算符:输出左边和右边的梯度平均值
公式推导:
\begin{split}
\frac{\partial f\left(x,y\right)}{\partial x} \\
&\approx\frac{1}{2}\{(f\left(x+1,y\right)-f\left(x,y\right) + f\left(x,y\right)-f\left(x - 1,y\right)\}\\
&\approx\frac{1}{2}\{f\left(x+1,y\right)-f\left(x - 1,y\right)\}
\end{split}
经典的边缘算法:Sobel算子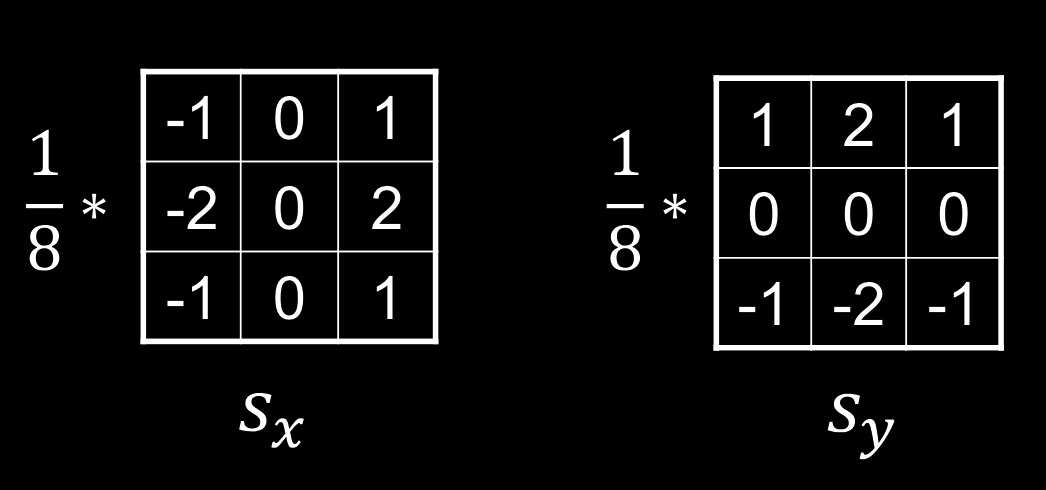
- $S_x$:左右和左上右上,左下右下的方向导数。
- $S_y$:同理
梯度:$\nabla\mathbf{I}=[\mathbf{g}_\mathbf{X}\quad\mathbf{g}_\mathbf{y}]^\mathbf{T}$
强度:$\mathrm{g=(g_X^2+g_y^2)^{1/2}}$
方向:$\theta=\operatorname{atan2}(\mathfrak{g}_\mathrm{y},\mathfrak{g}_\mathrm{x})$
Sobel古老的例子:X windows

右边的图像是做了阀值化thresholded
著名的边缘算子: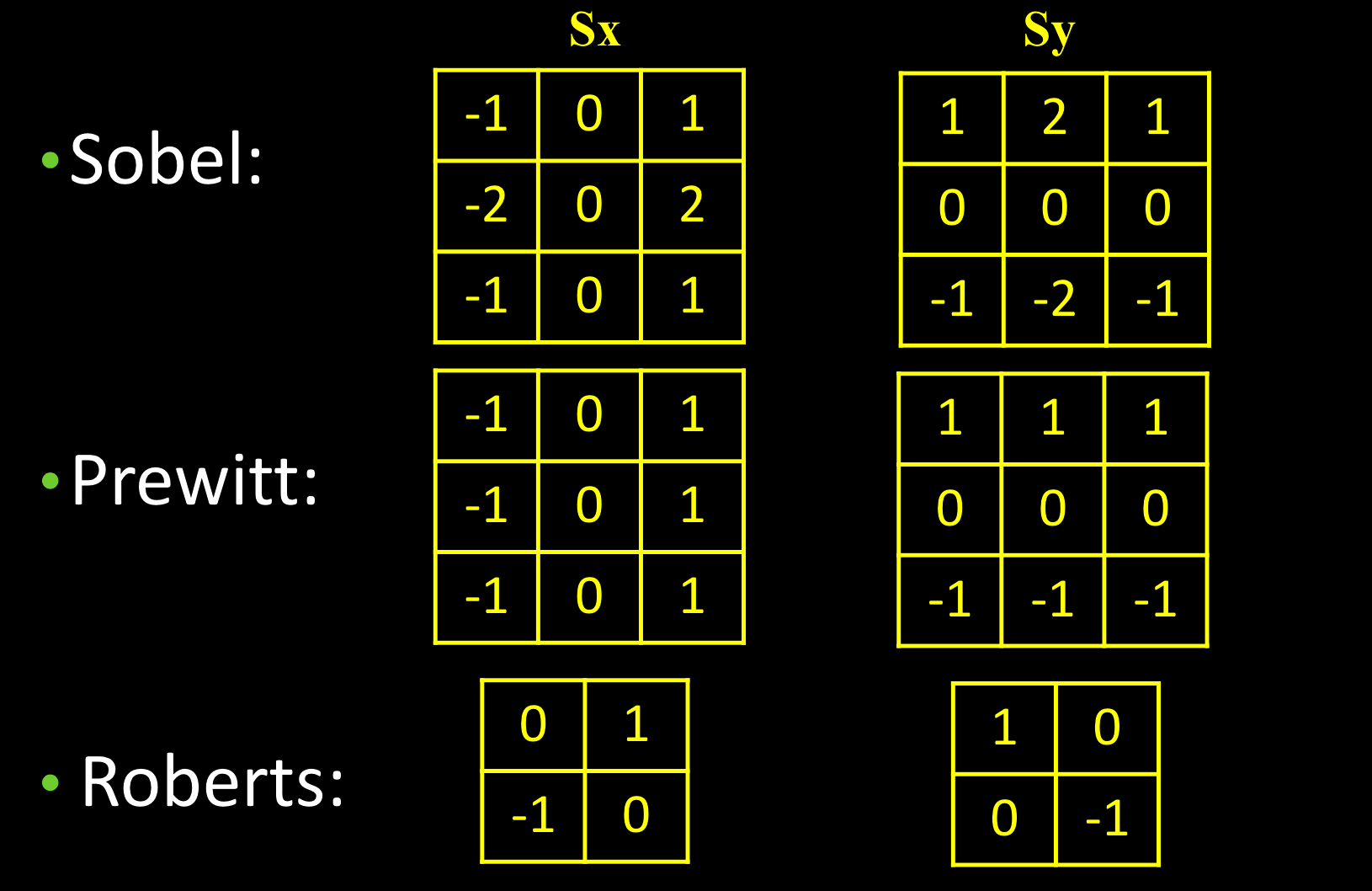
现实世界
上述算子在现实中不会起作用,噪声太多。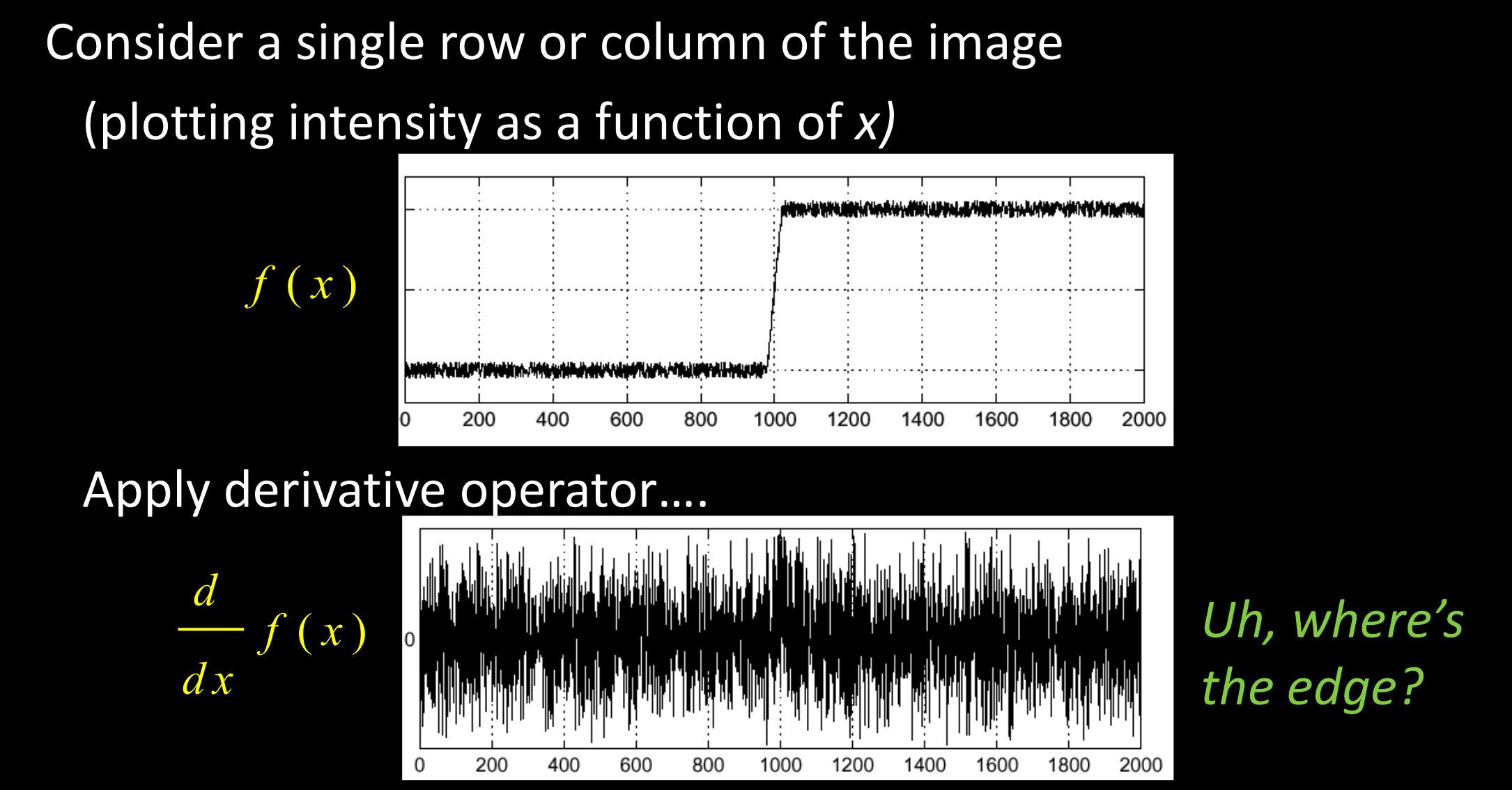
所以必须先处理噪音,在边缘化。
解决方案:平滑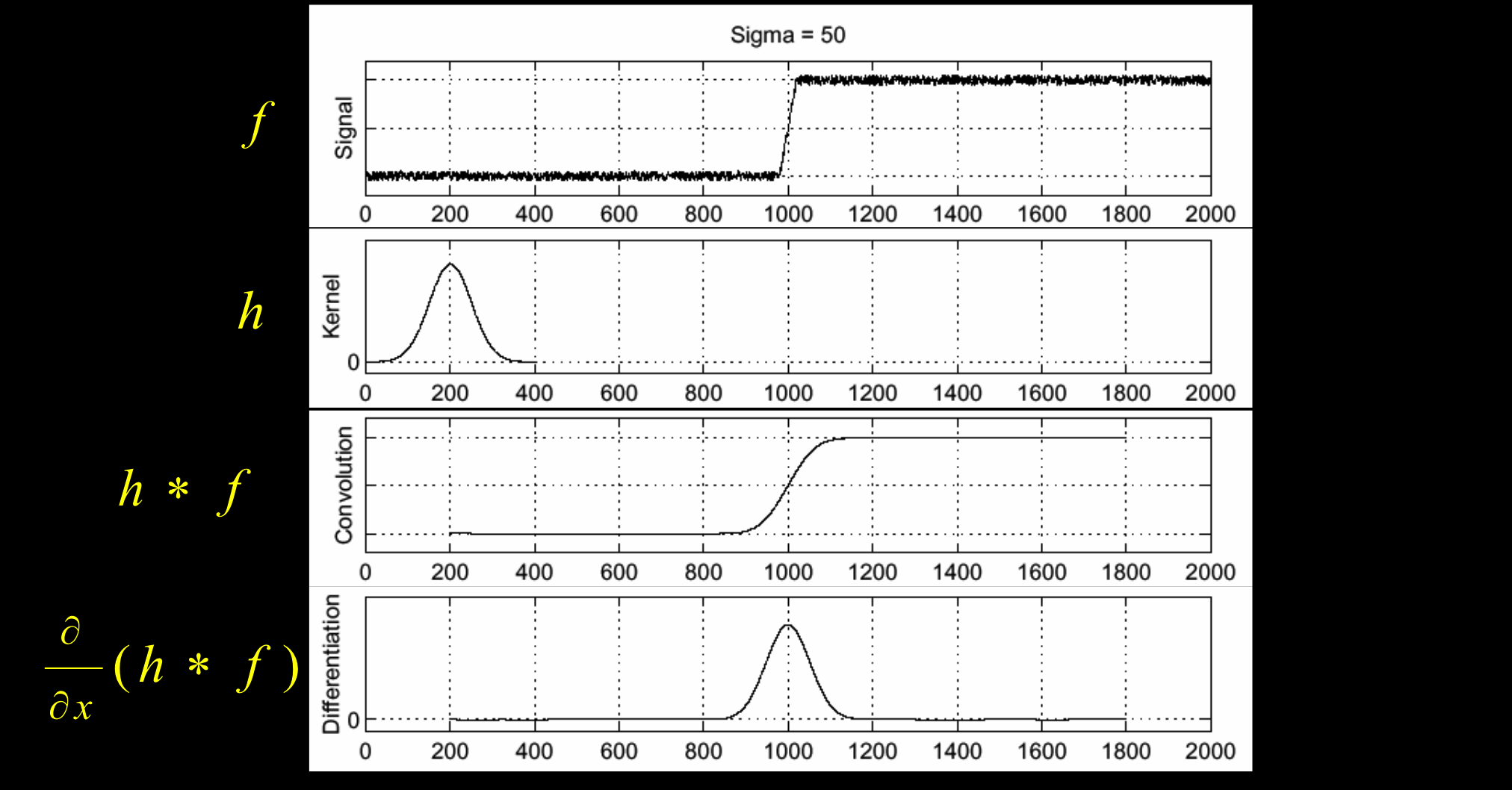
山峰就是边缘像素。
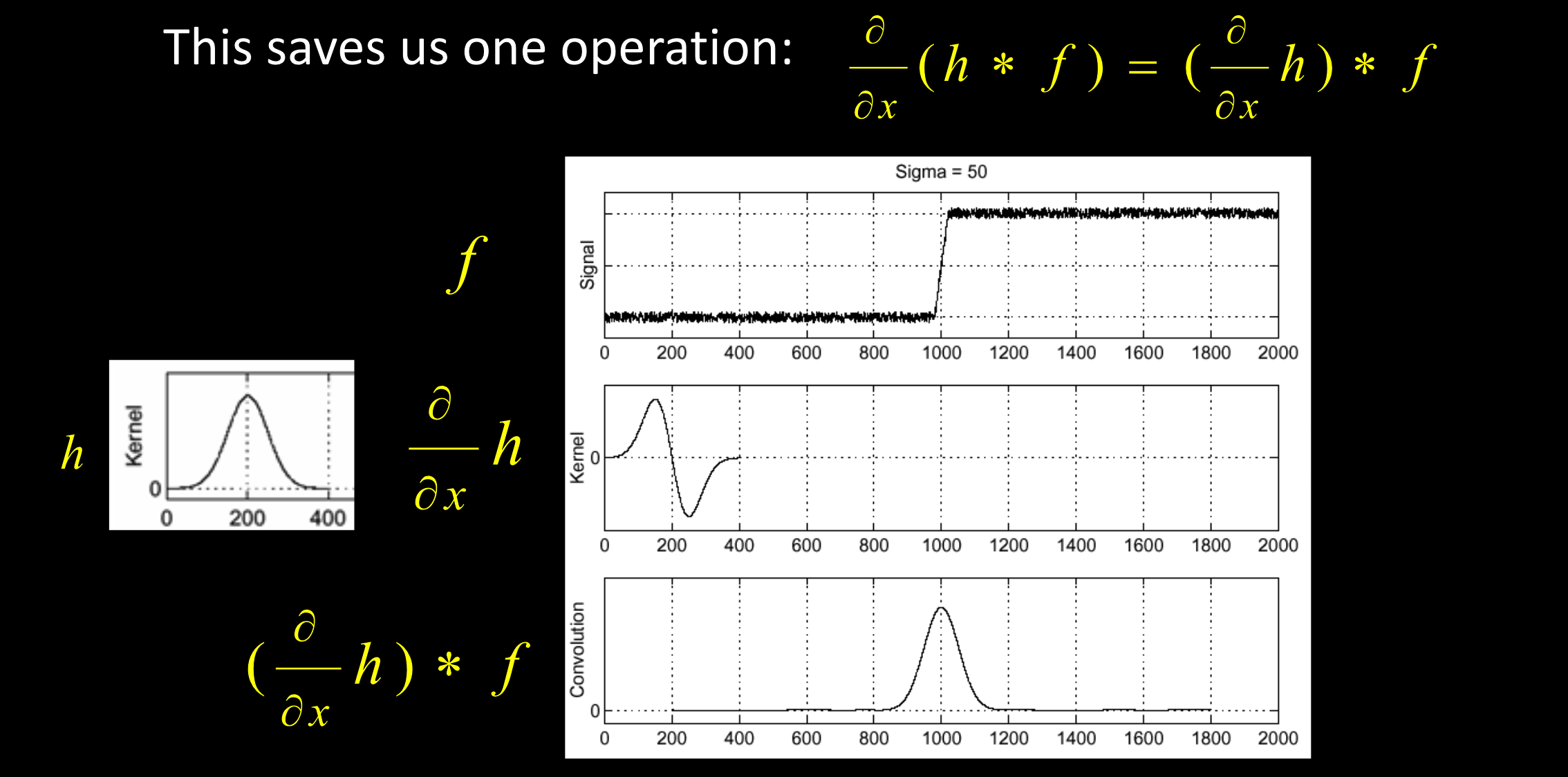
算子的线性结合性
利用卷积的求导公式: $\frac\partial{\partial x}(f*g)=\frac{\partial f}{\partial x}*g$
二阶导数
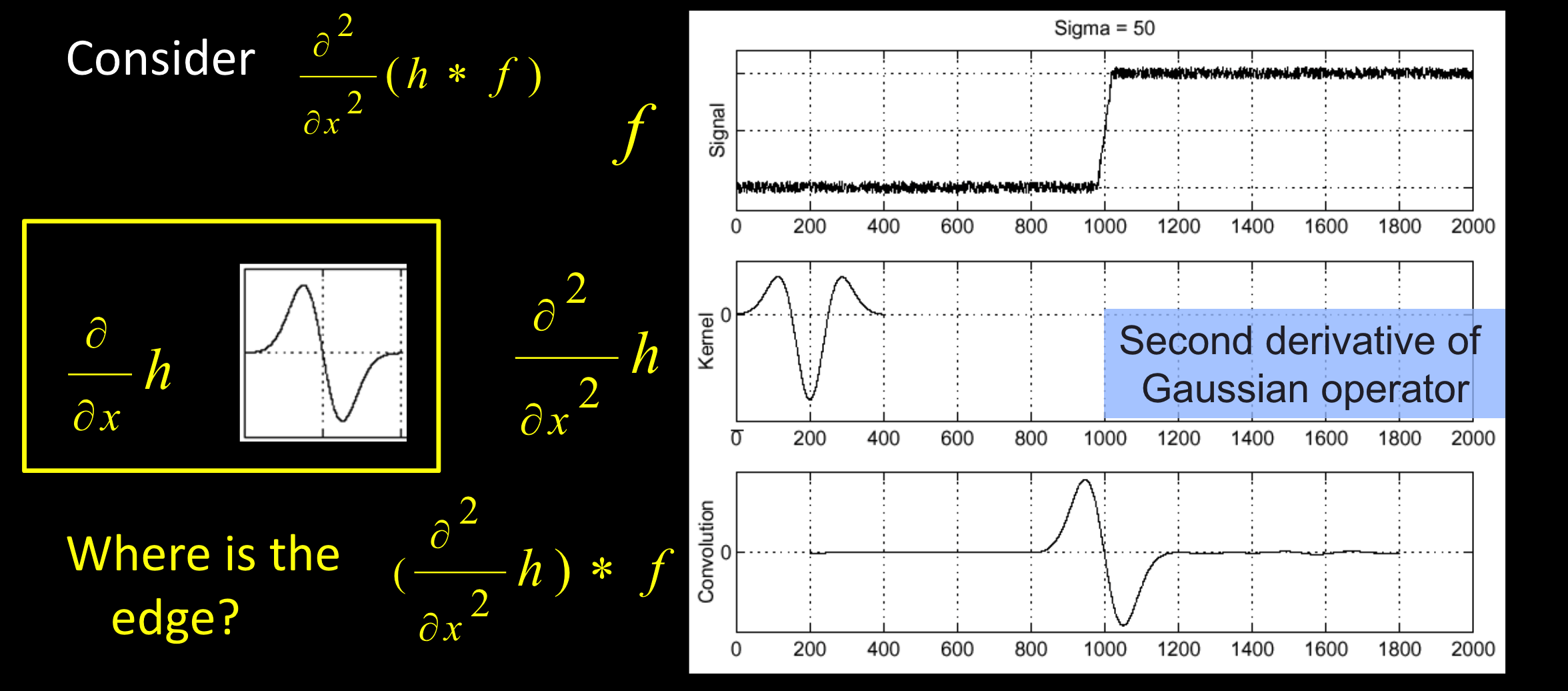
零强度的位置就是边缘像素,不需要再找峰值了
2D边缘检测
二维高斯滤波器的导数
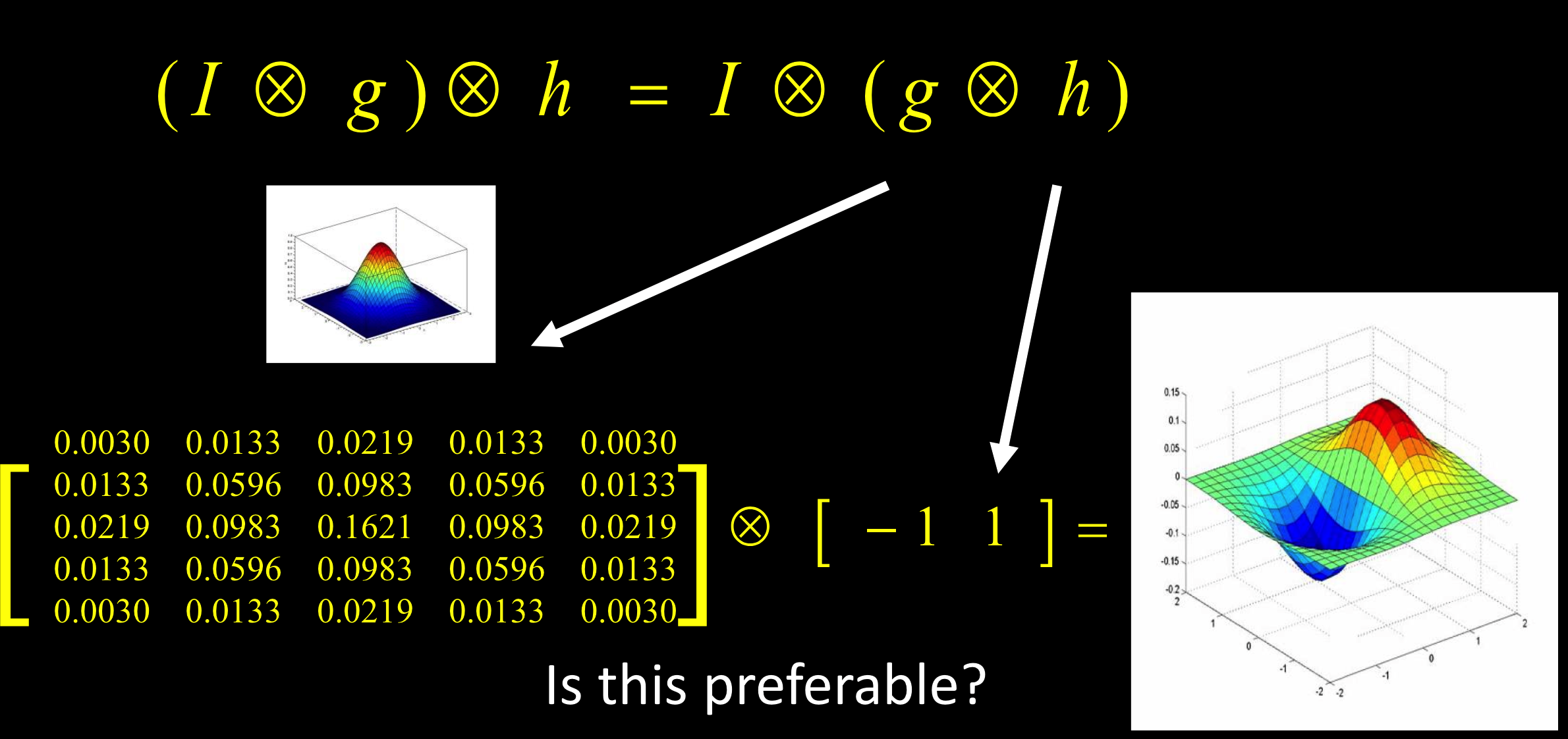
- 公式:$(I\otimes g)\otimes h=I\otimes(g\otimes h)$
根据结合性 - $h$: 只对x求导
- $g$: 高斯平滑
高斯滤波器的导数: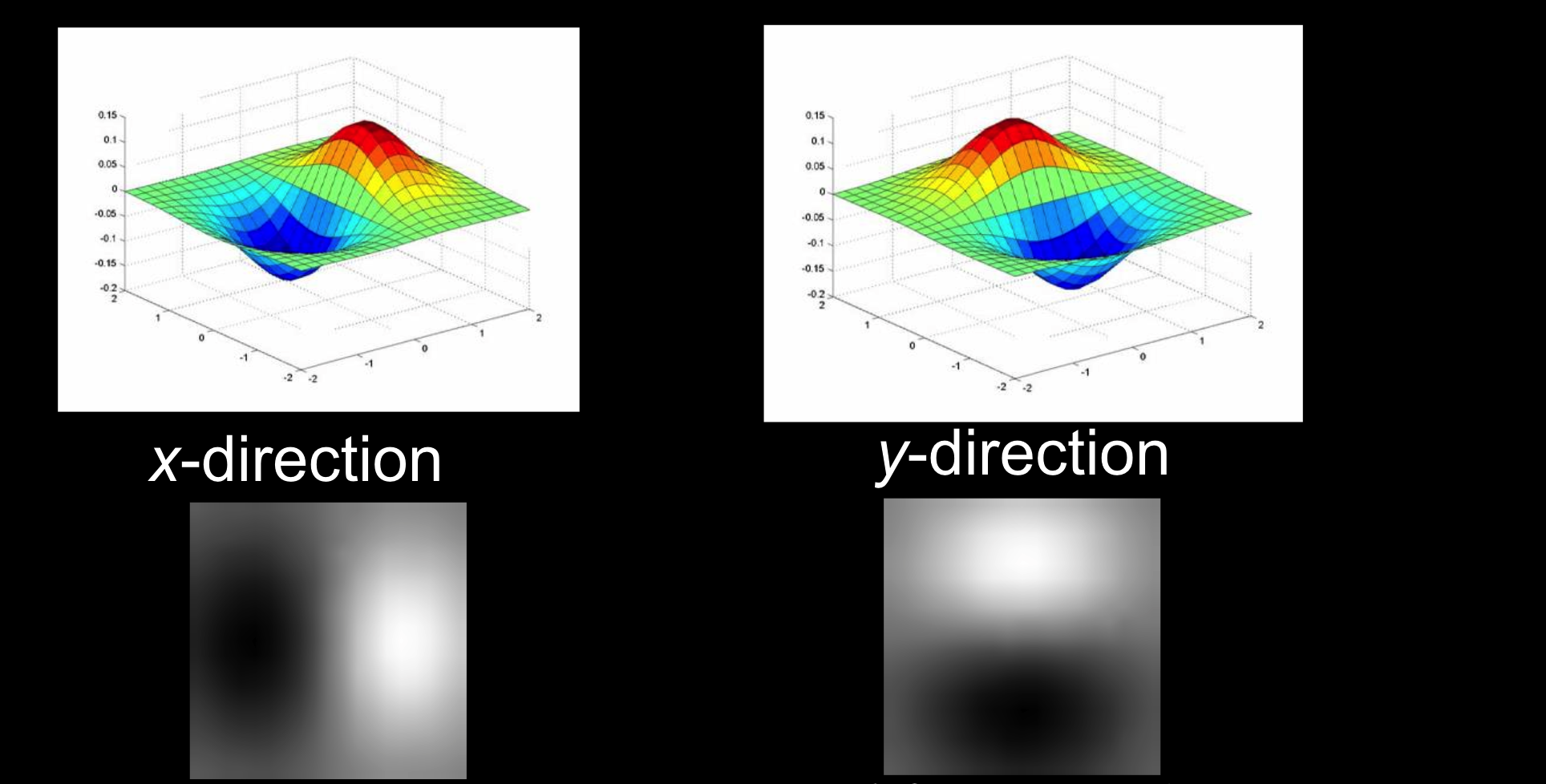
- 左图:可以看出是一个相关操作,因为往右增为正方向。
- 右图:
sigma的大小:
不同的sigma对于图像边缘的影响:较小的值,有精细的特征,而较大的值仅仅检测到较大尺度的边缘。
如何找到边缘?
Canny算子:
- 对高斯图像进行滤波
- 找幅度最大的方向,进行非极大值抑制,即细化操作
- 连接操作,将边缘连接起来
定义了两个阀值:极大阀值和极小阀值
原图:
梯度图:
阀值处理图:消除一部分梯度够高的像素
细化处理:(非极大值抑制)
做法:某个局部有很多梯度点,只保留极值最高的点,抑制非极大值
为什么要进行细化操作: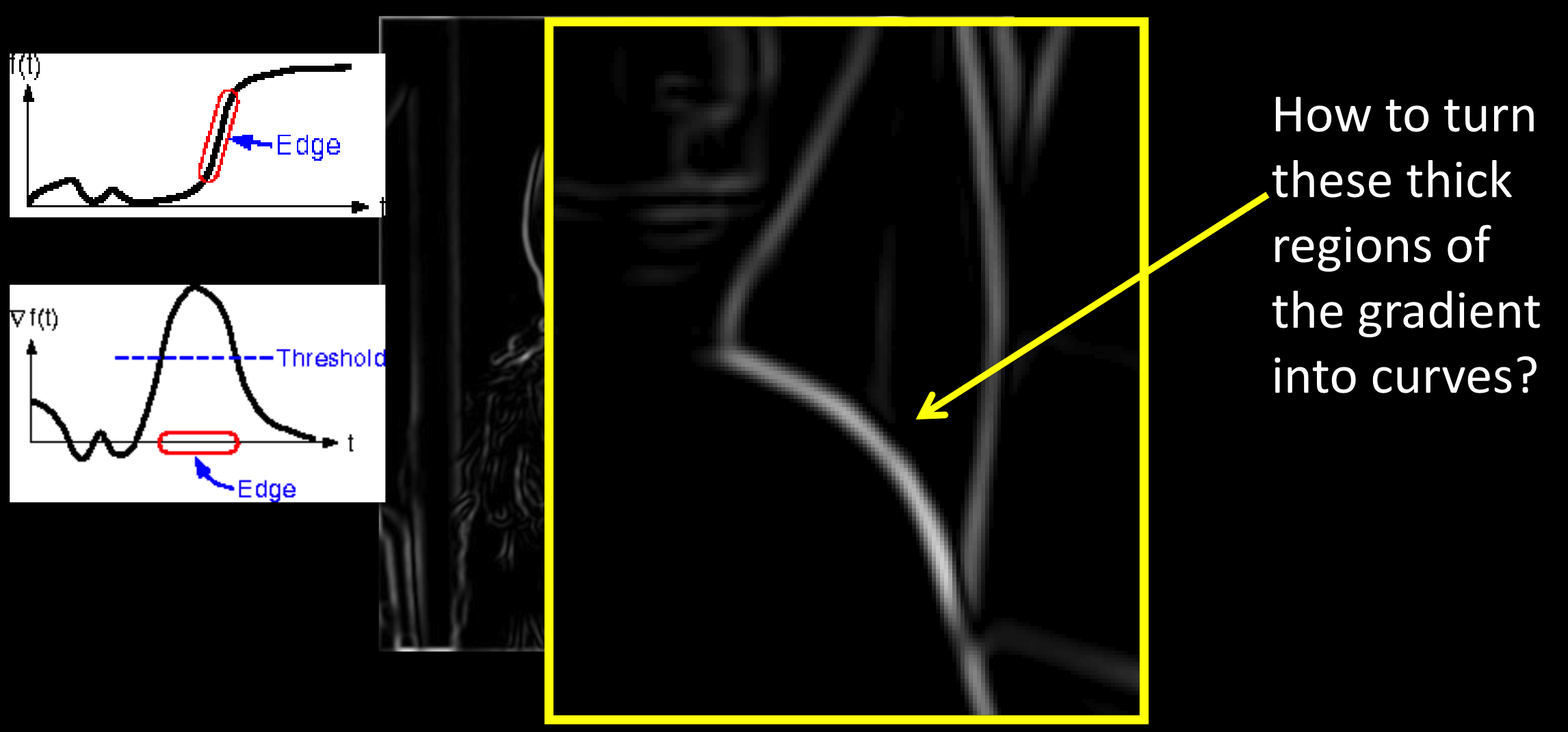
超过阀值的粗部分,只保留极大值,细化为一条直线。
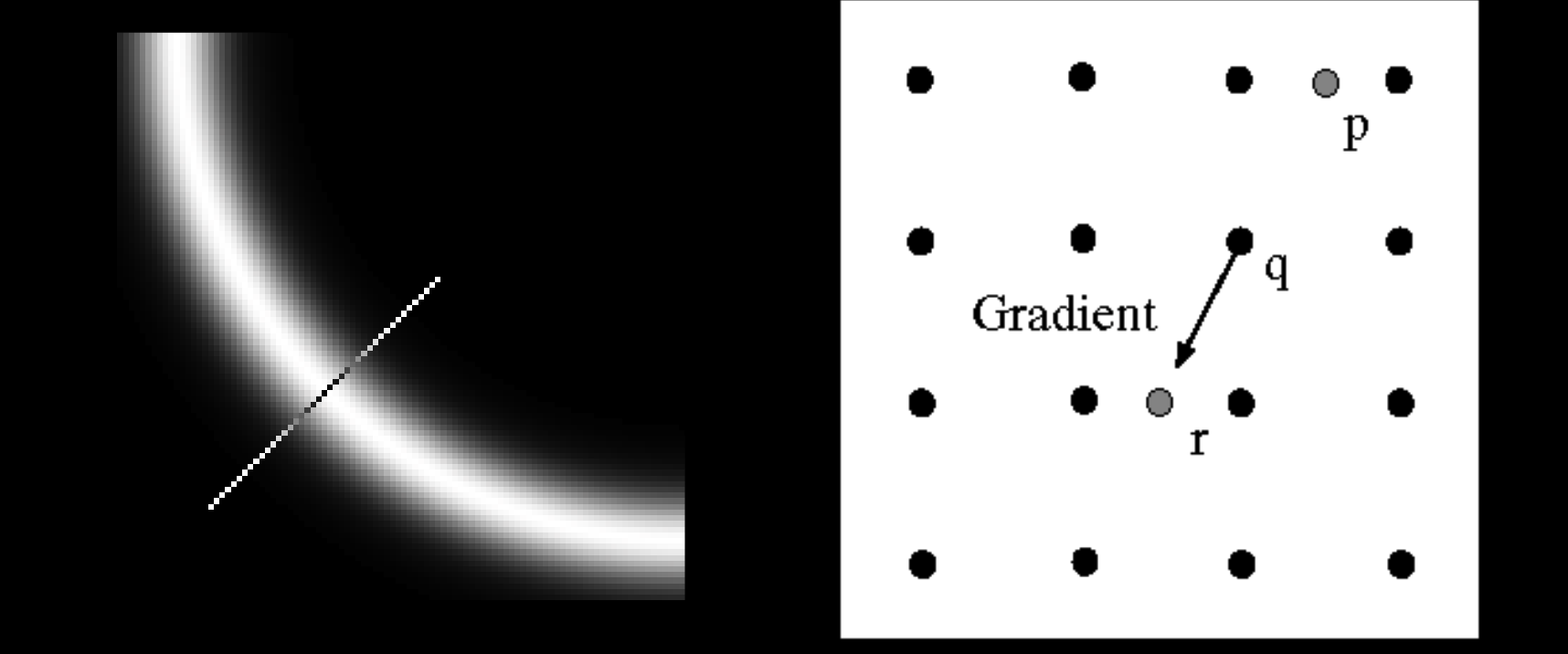
在梯度方向找到极大值
另一个问题:下巴的边缘没有检测出来?
阀值太高,下巴的梯度没有通过阀值。
Canny阀值滞后:
- 用高阀值检测边缘,找出强边缘像素
- 连接成强边缘
- 应用低阀值找出弱边缘像素
- 把强边缘延长到弱像素上
如果一条边缘上只有弱边缘像素,就不是一个需要的边缘
强边缘可能会穿过一些弱边缘像素
Canny 算子的结果:
什么样的边缘图是好的?取决于你想用什么样的边缘图。
简单的二维边缘检测滤波器
偏导有多种顺序
拉普拉斯算子用于求二阶偏导
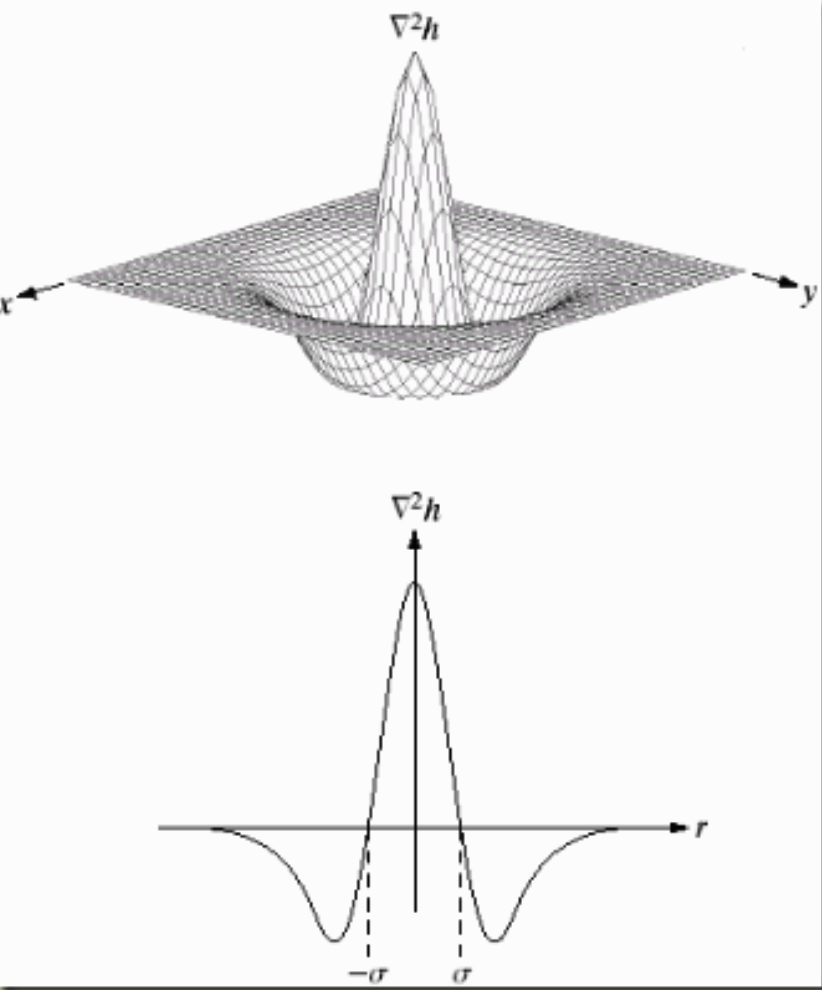
公式:$\nabla^2h^2=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2}$
- $\nabla^2$: 拉普拉斯算子
- 0为边缘像素
霍夫变换(Hough transform):直线
如何找到任意形状?
参数模型(Parametric model)
参数模型是一个类
直线匹配:
边缘图: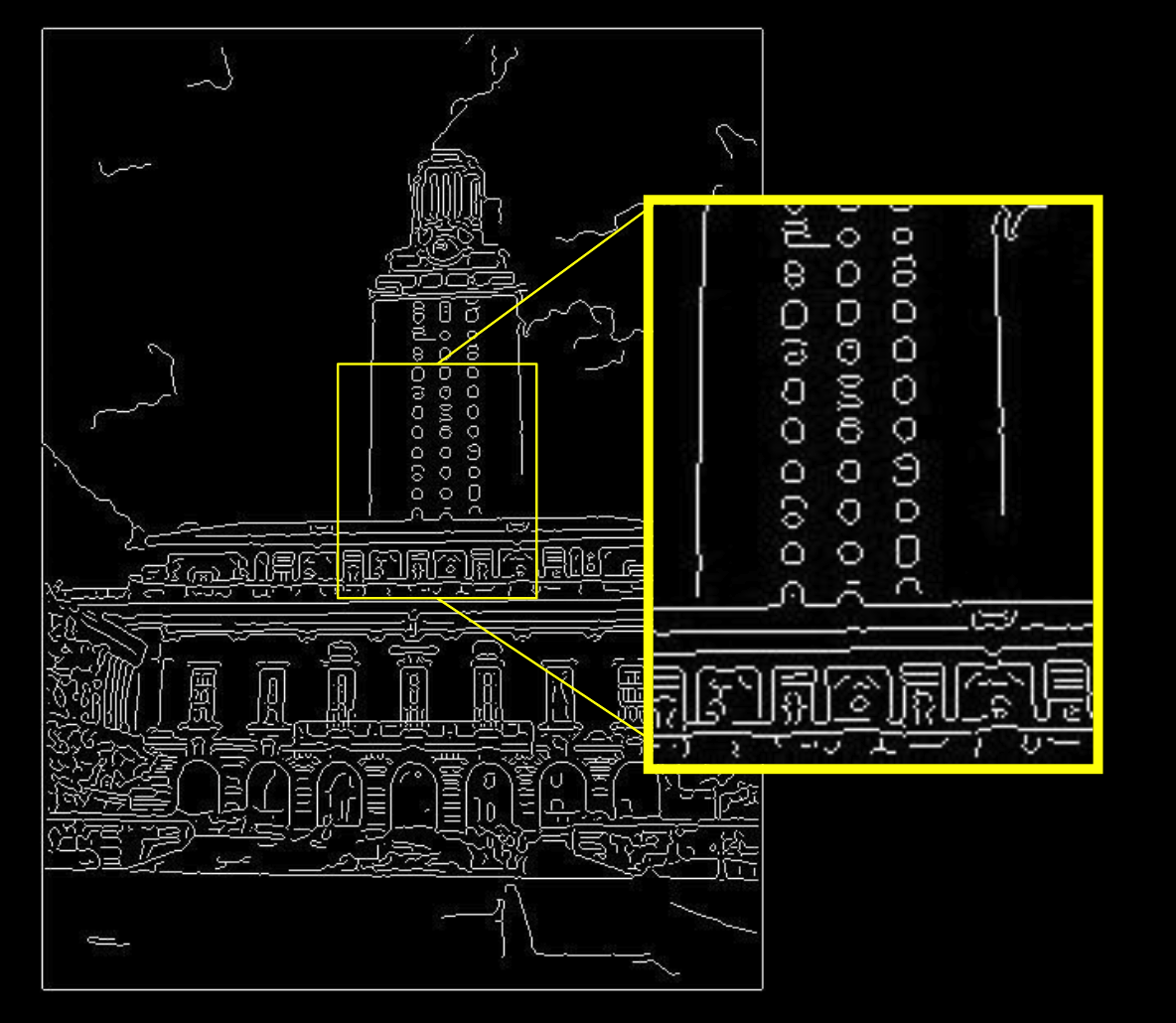
困难:
- 有很其他形状,多种模型
- 线不连续
- 噪音
投票:
- 每个像素点对有用模型投票
- 找出最高的模型
原因:有很多无效的像素点,但只要有真正的像素点投票是有效的,选出匹配的模型,就可以淘汰掉噪音。
拟合直线的几个问题?
- 给定一些点,哪些是一条线
- 有多少条线
- 有哪些点是属于线的
霍夫变换:一种投票技术,可以解决上面的问题
- 每个边缘点都会投票给兼容的线
- 找票数最多线
- 追踪票,可以找到属于线的点有哪些
霍夫空间Hough (parameter) space
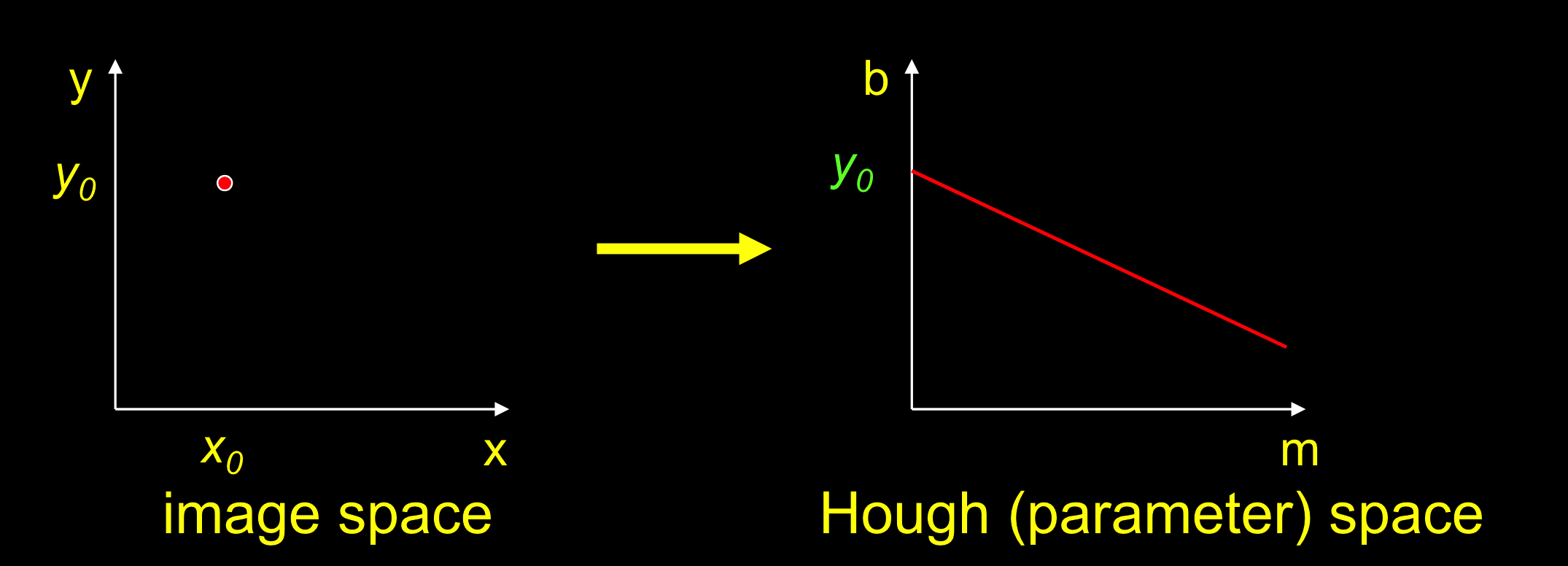
对于一个点$(x,y)$,穿过这个点的直线为:$y_0=mx_0+b$,$m$,$b$为任意值。
所以对应霍夫空间的函数为:$b^2=-x_0m^2+y_0$
将空间中的一点,对应到霍夫空间中的一条直线
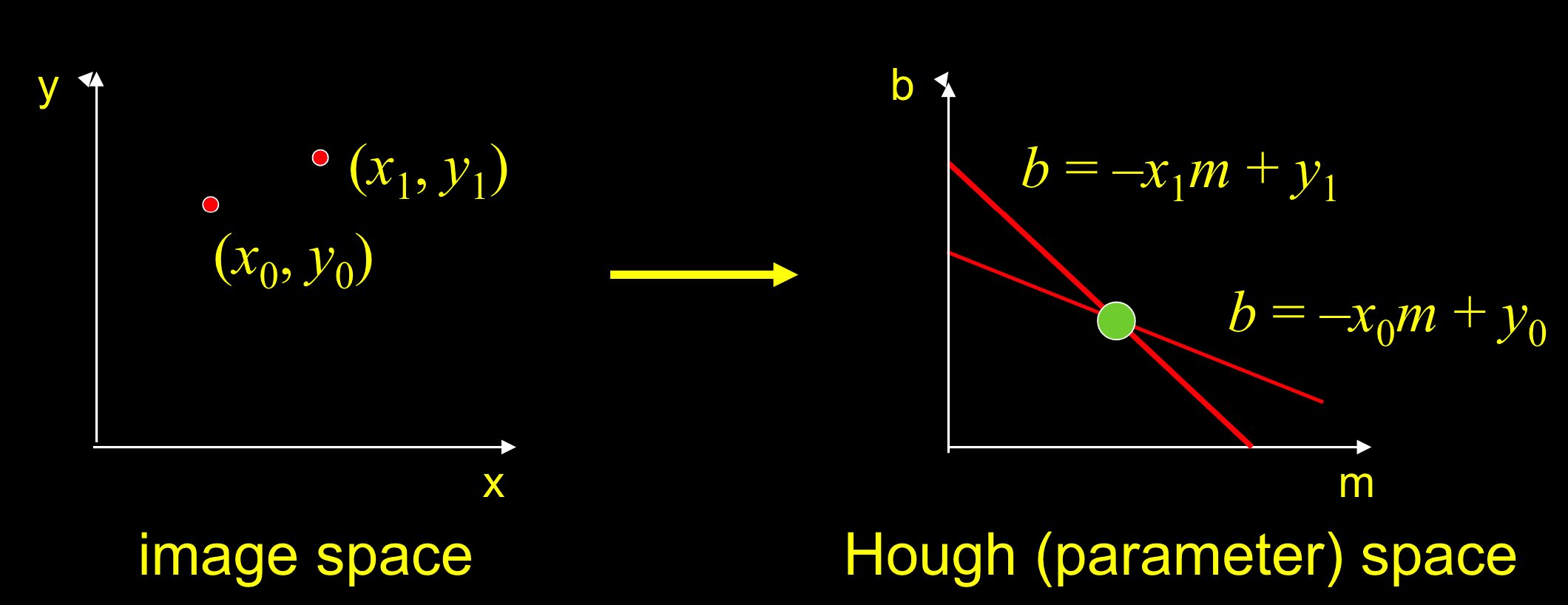
- 霍夫空间中的交点,对应的参数,是过两点的直线
- 这就是从点中找线的方法
霍夫算法
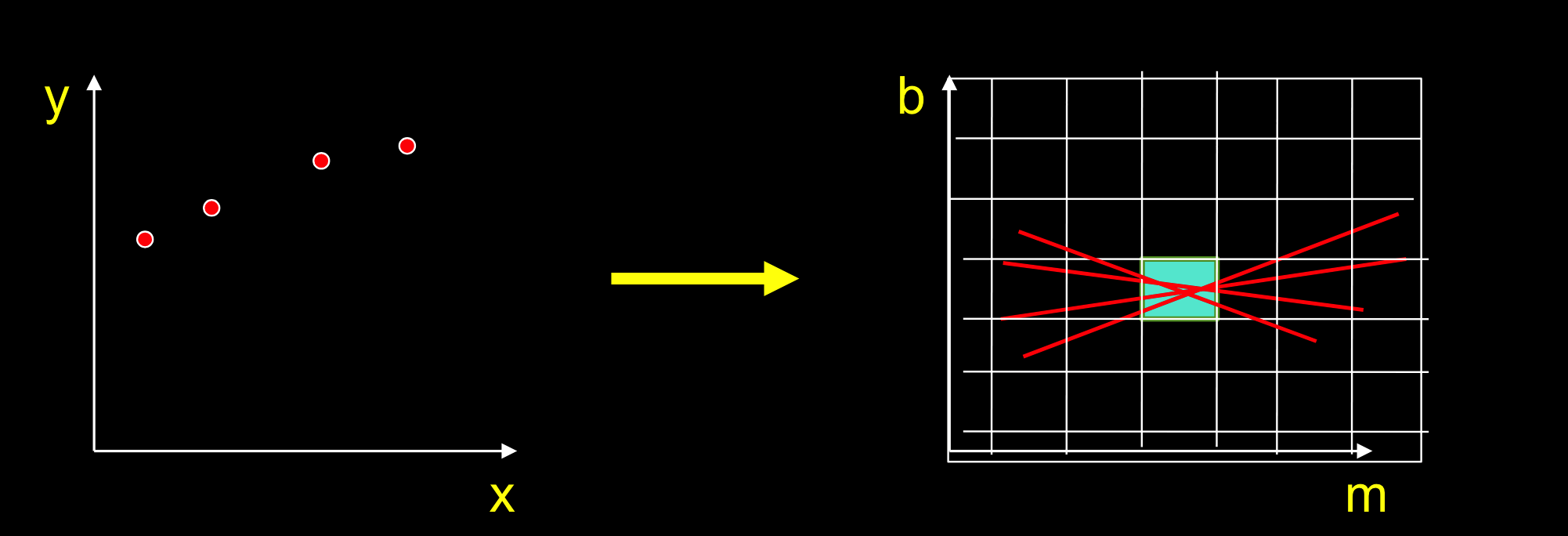
点对应于霍夫空间中的线:
- 每个点都对自己经过的分区投票
- 票数最多的就是线
具有偏差
为了防止出现垂直直线的表示,采用极坐标法表示图像
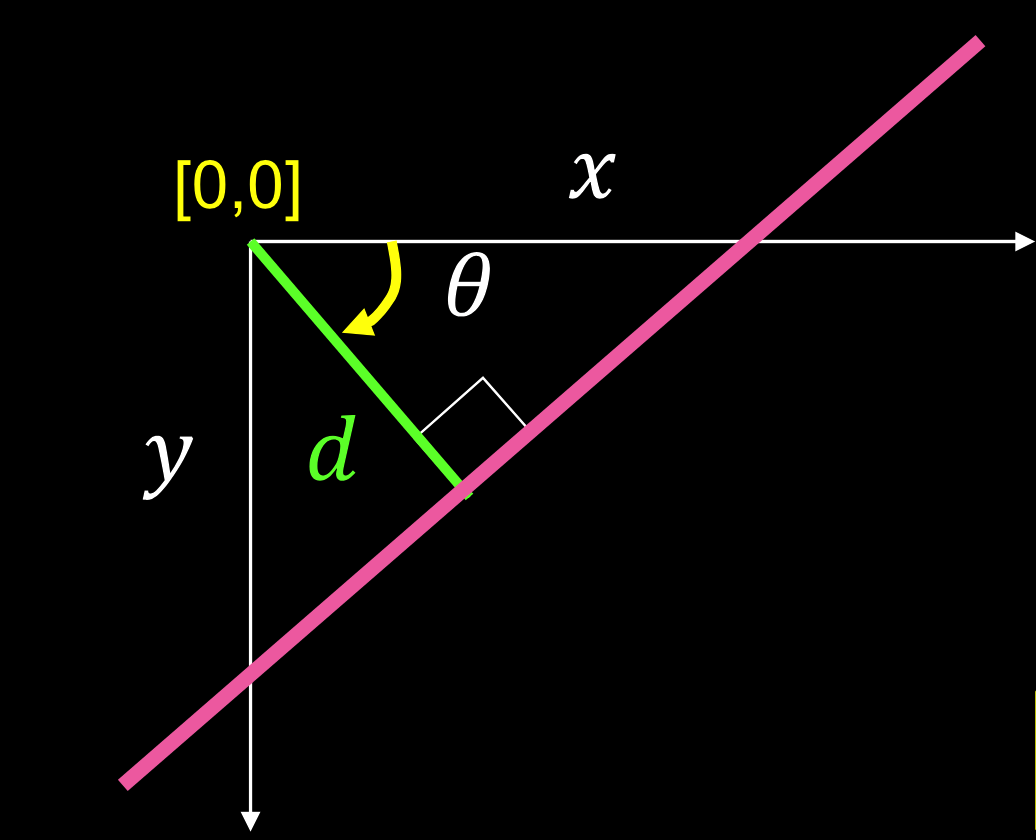
- $d$:原点到点距离
- $\theta$: 表示到$x$轴的角度
- $\quad x\cos\theta+y\sin\theta=d$
可以表示任何的直线
图像空间中的点是霍夫空间中的正弦曲线
基本霍夫变换算法
霍夫累加器数组(收集投票的数组):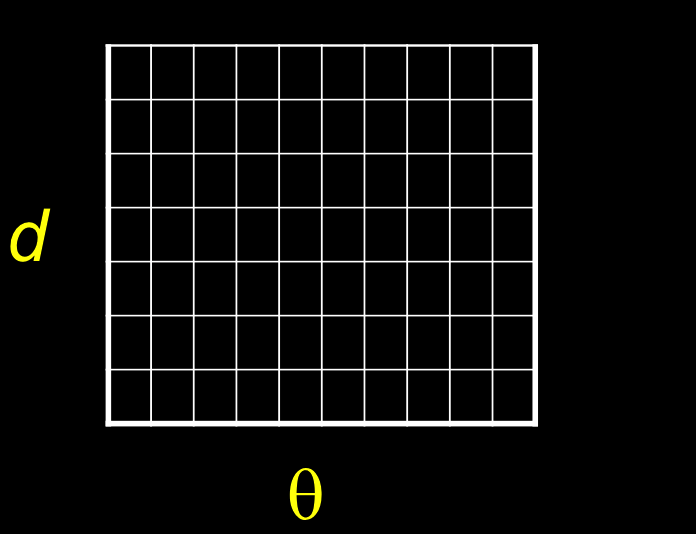
霍夫算法:
霍夫变化的复杂性:
空间复杂性和时间复杂性都很大
直线的霍夫空间:
无噪音的直线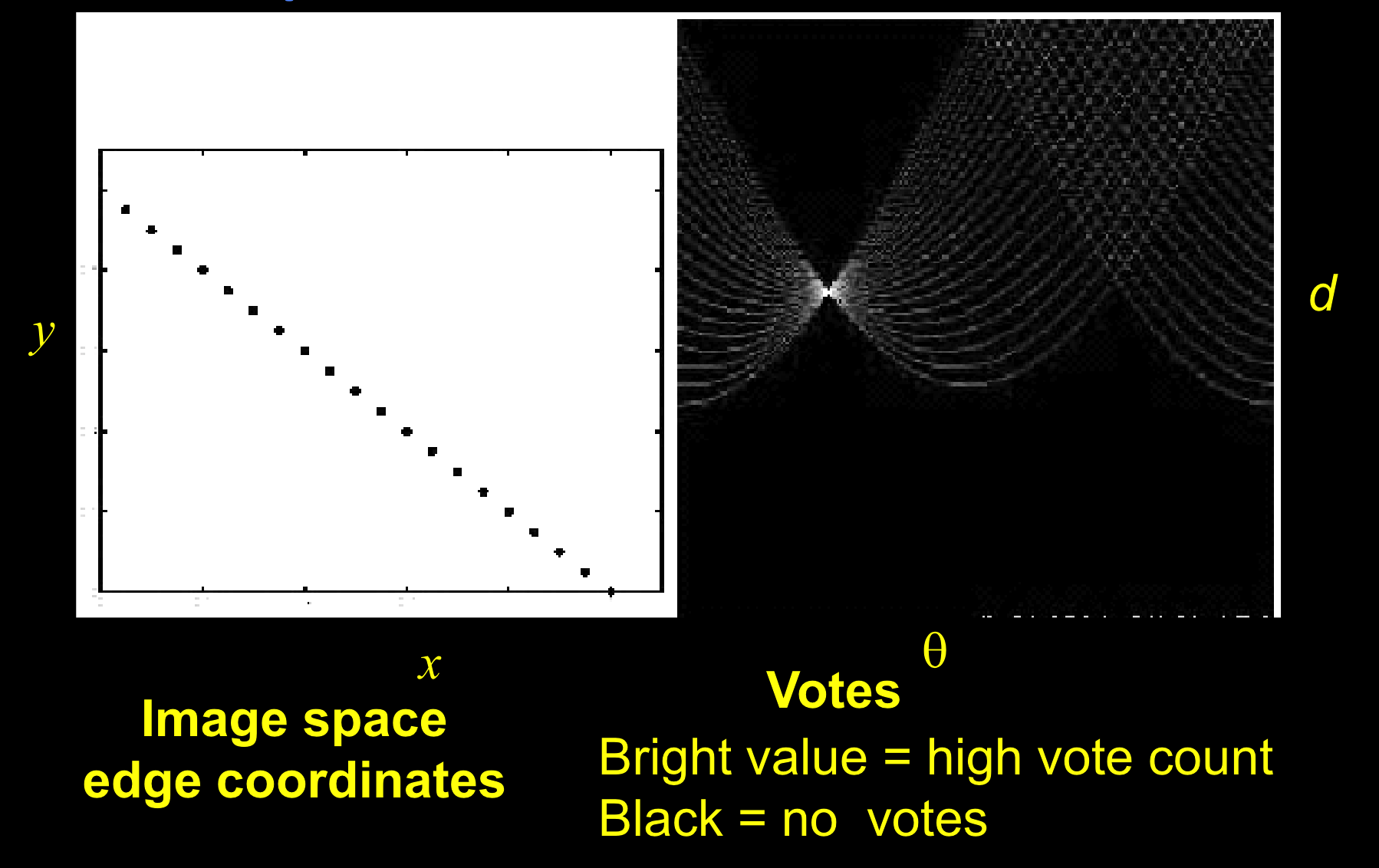
最亮的点:是像素最多的直线
正方形的霍夫空间: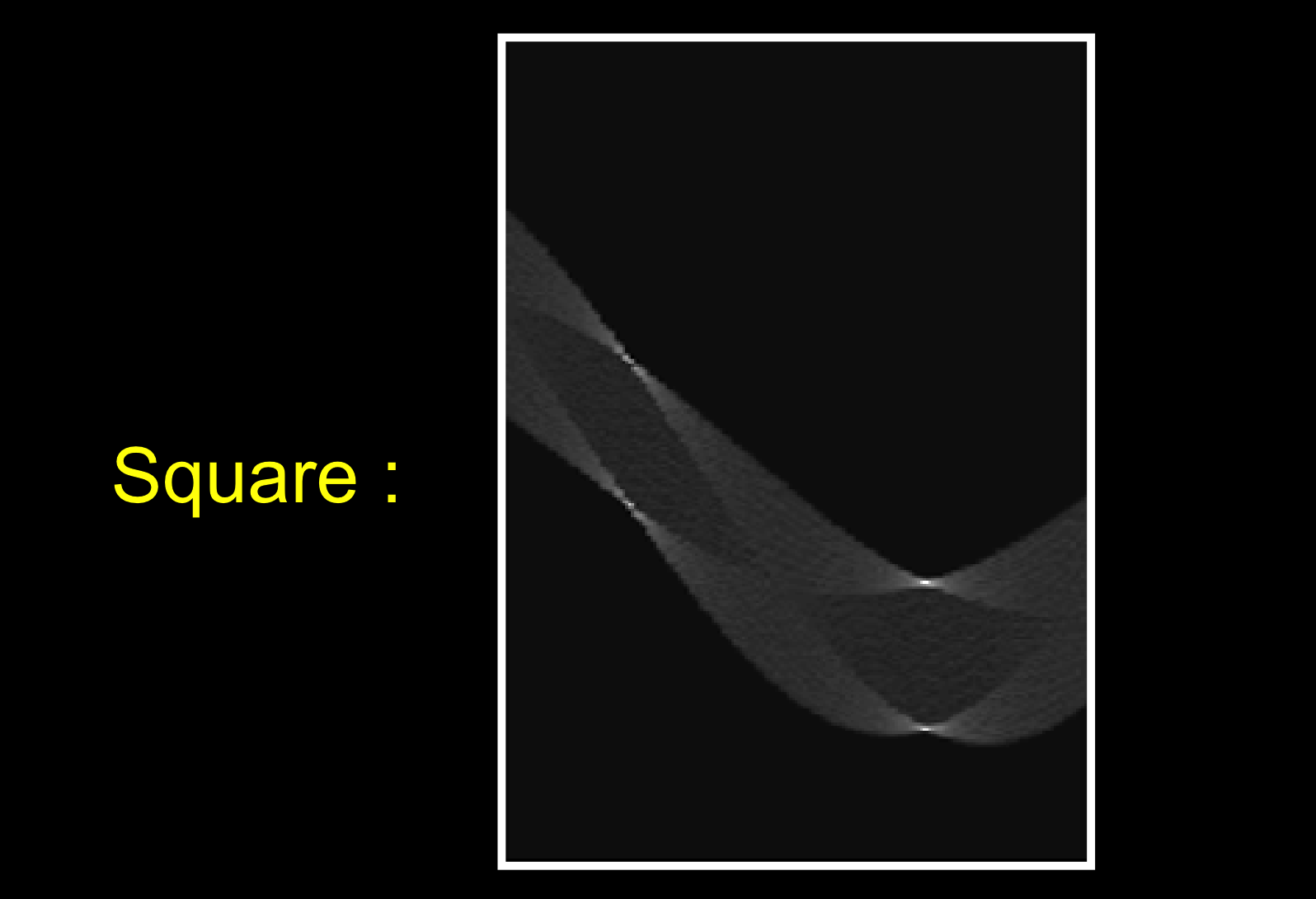
噪音对霍夫变化的影响
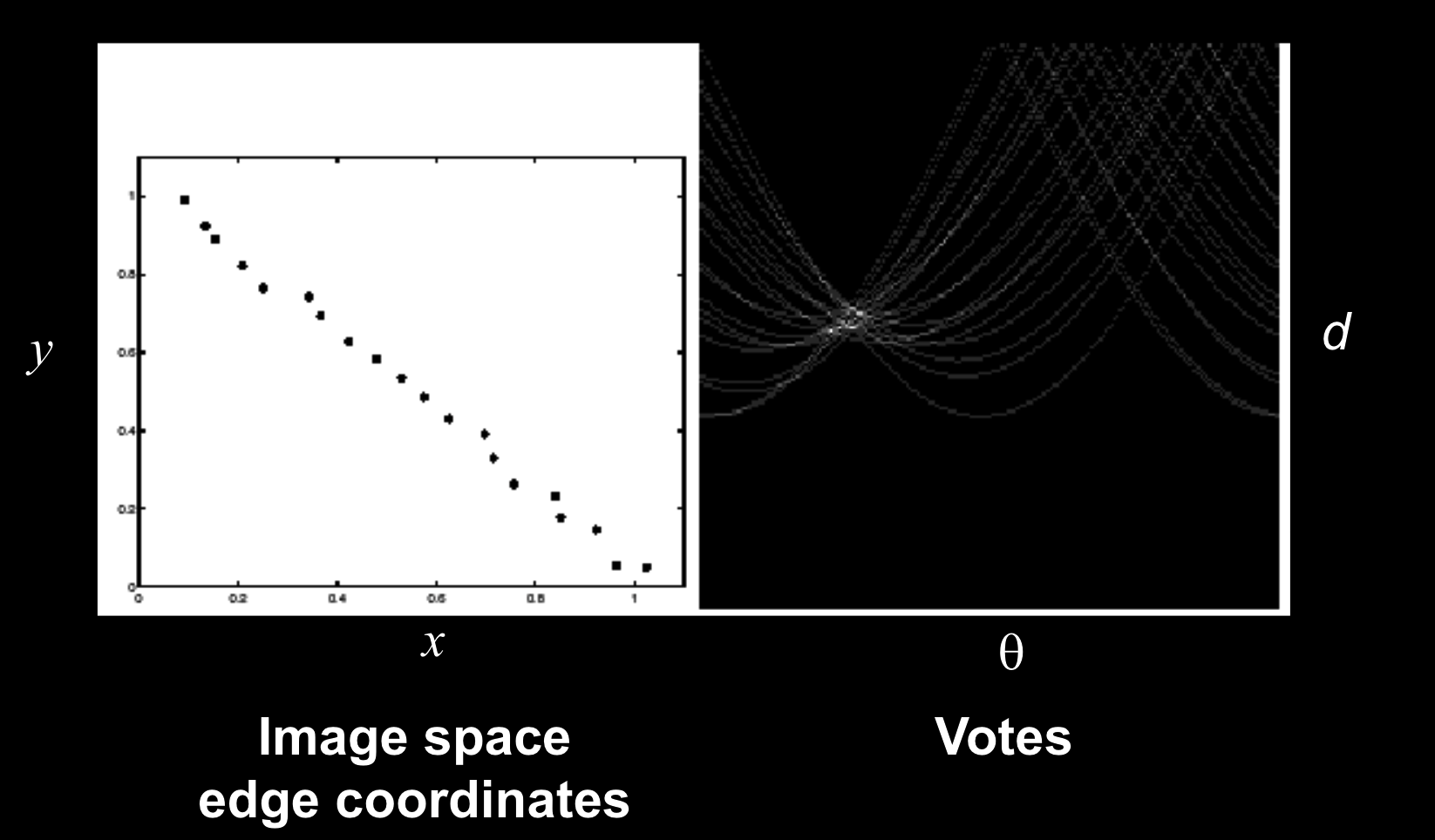
峰值不明确了
更多的噪音: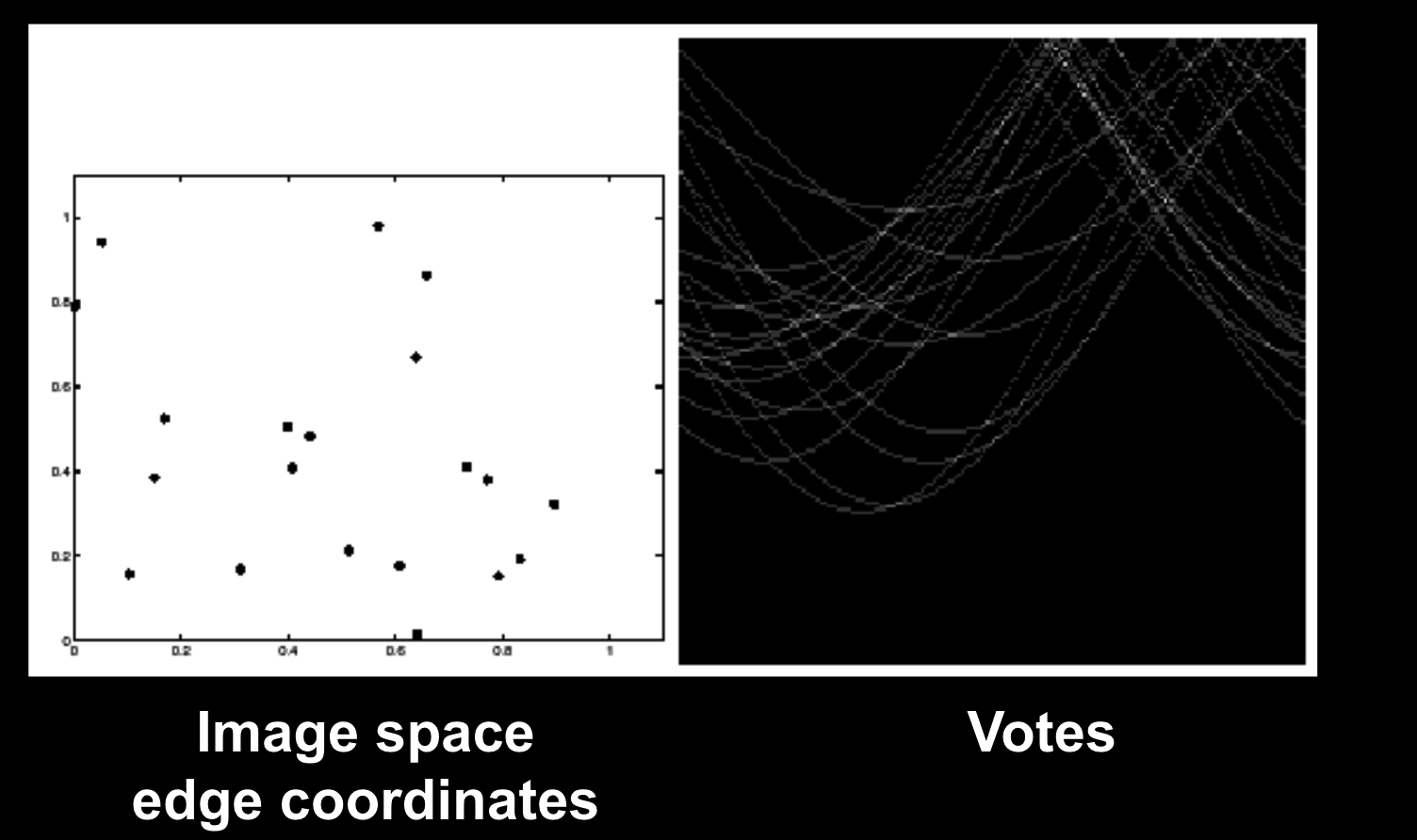
霍夫变化的扩展
使用梯度优化霍夫变换算法
优化的霍夫变换的地方?
扩展二:
改变阀值
扩展三:
改变投票箱的大小
扩展四:
相同的操作可以用的其他形状
课上的算法对现实是不起作用的
论文中的算法也是不起作用,要把故事讲得好听
关键是理解原理
霍夫变换(Hough transform):圆
圆的方程:$\left(x_i-a\right)^2+\left(y_i-b\right)^2=r^2$
圆的霍夫空间: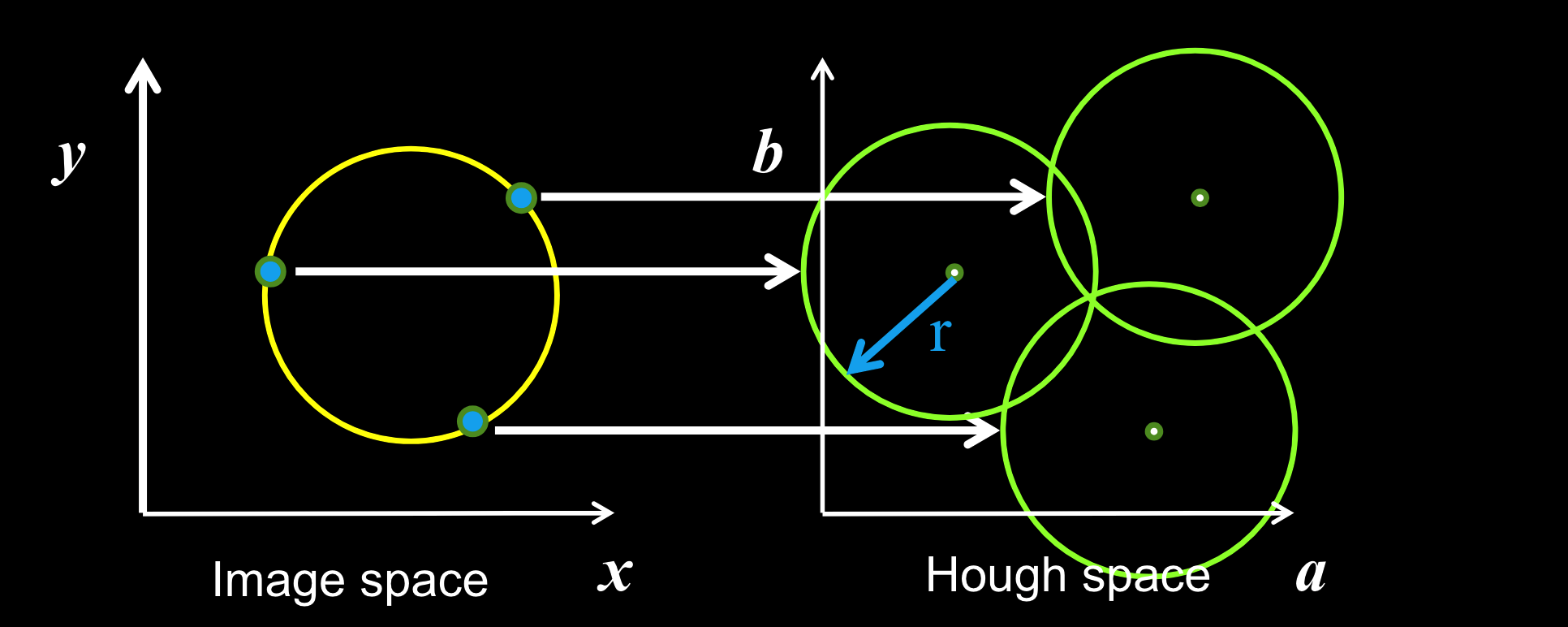
使用更大的投票箱:
圆的霍夫变换
投票箱在3D空间中: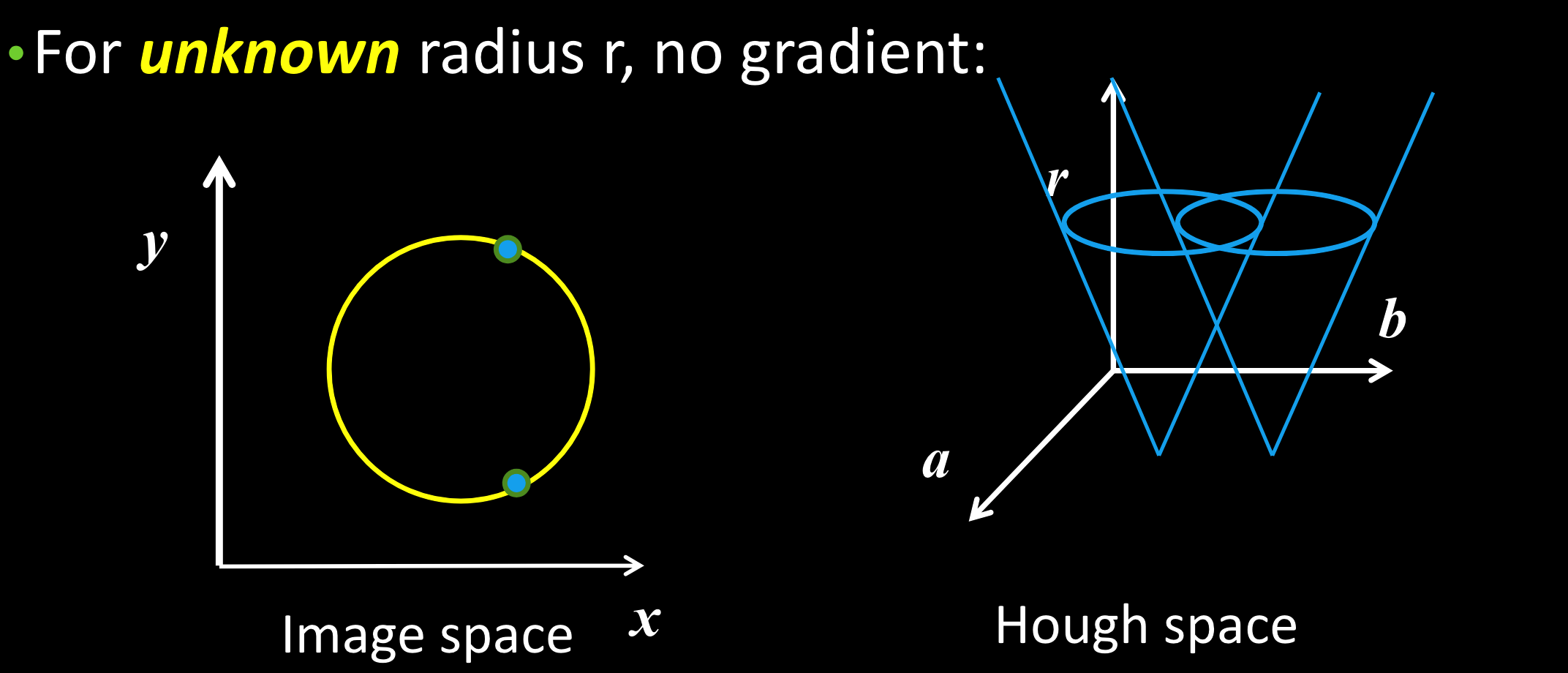
梯度优化: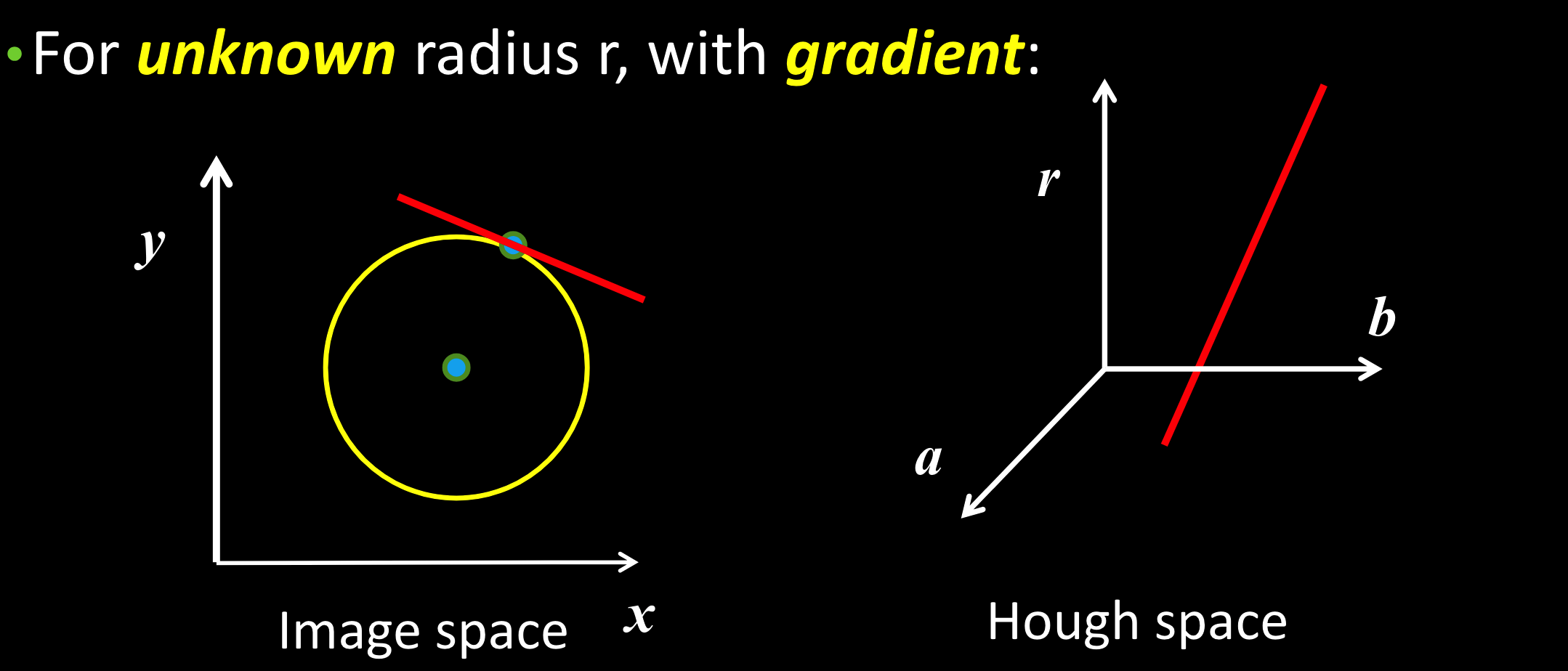
- 过这点的圆心只可能在:点和圆心的连线,即梯度垂线上
- 这样就过滤掉其他位置的圆心投票
算法:
投票的实用技巧
- 剪枝,不要投没用得票
- 选一个合理的投票网格
- 太大,投的错误太多
- 太小,噪音会影响
- 投票给临近的投票箱,类似累加器平滑
- 使用梯度优化投票
优点缺点
优点:
- 每个像素投票都是独立的,不受遮挡影响
- 噪音也不影响
- 可以在单图像找多形状
缺点:
- 参数的复杂性
- 非常规形状,投票很复杂
广义霍夫变换
非分析模型
霍夫表:
用于给非规则形状投票
建表: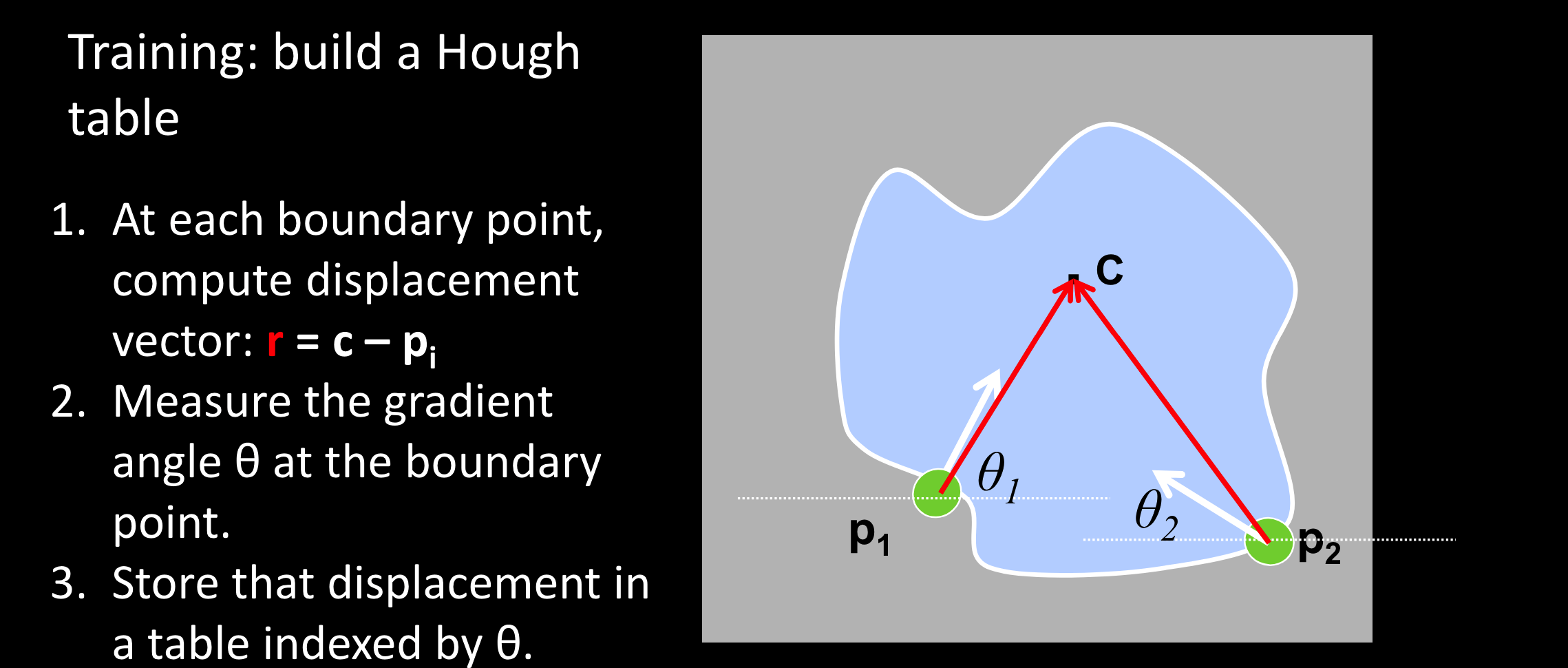
- $c$:是一个定位点
- $r$:位移矢量
- $\theta_1$: 梯度
- 把$r$放入由$\theta$索引的表
识别:
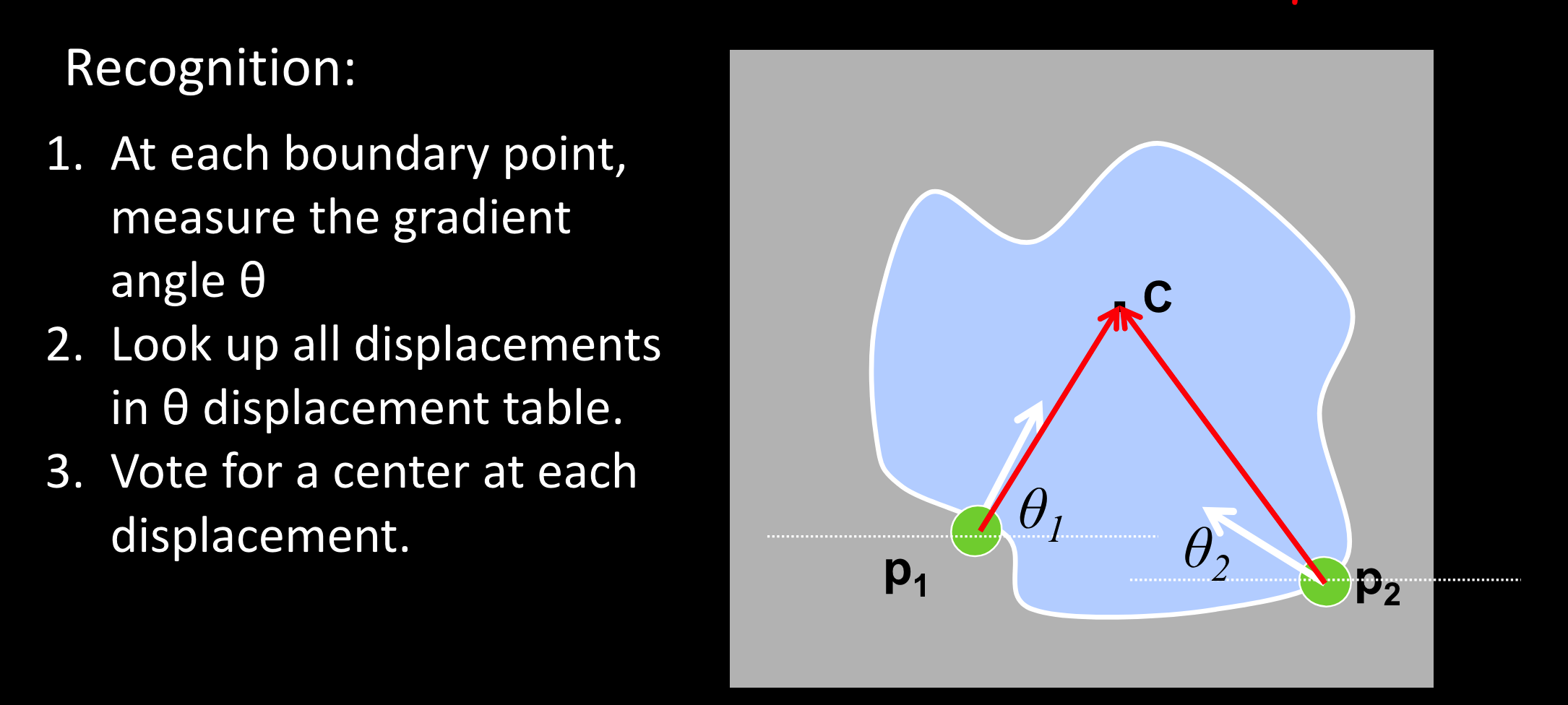
- 计算边界点的梯度方向$\theta$
- 在表格中找出所有该方向的位移向量
- 给位移向量的终点投票?
样例:
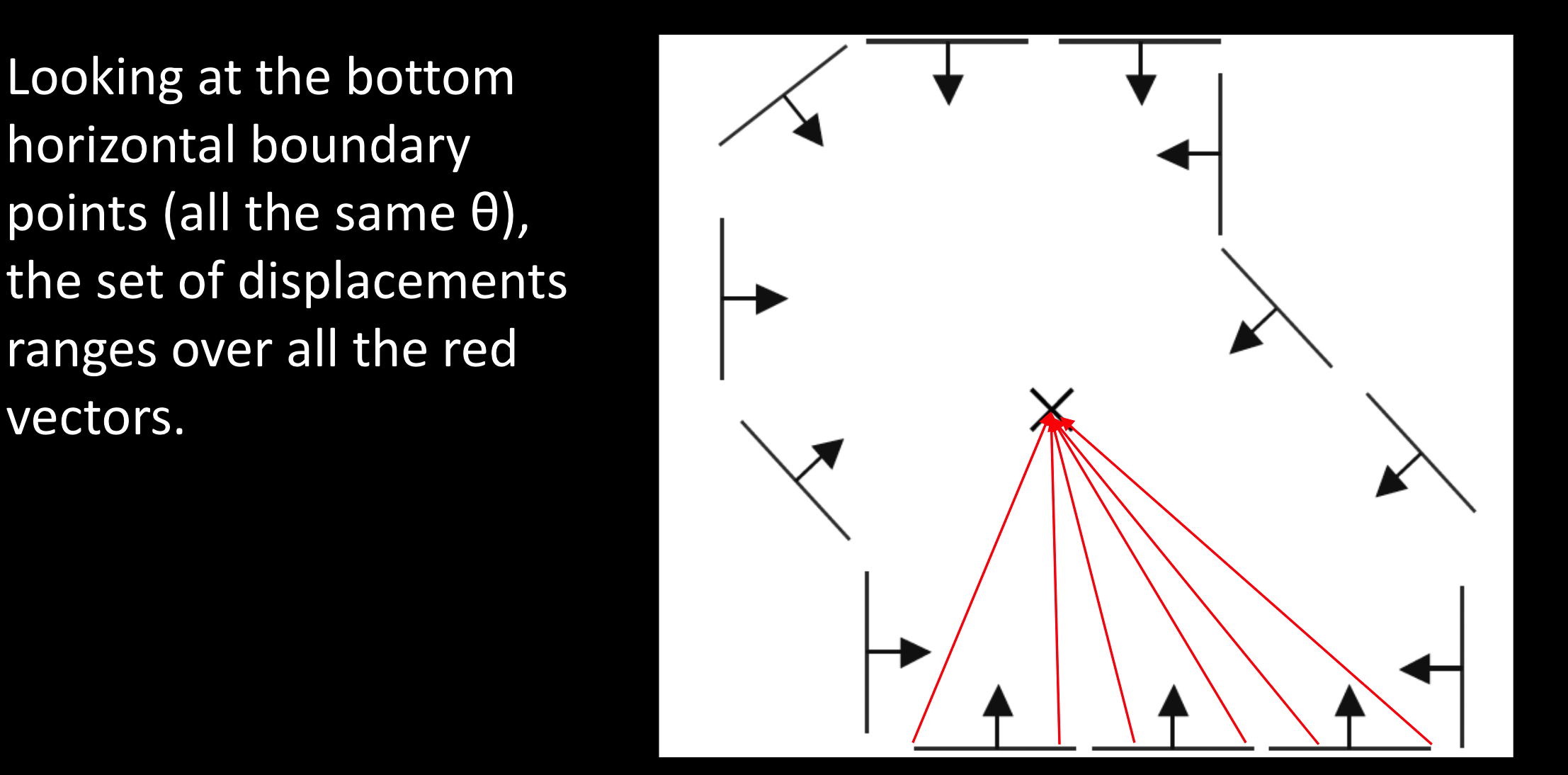
底部的边有相同的$\theta$,但是不一样的位移,对所有的位移投票。
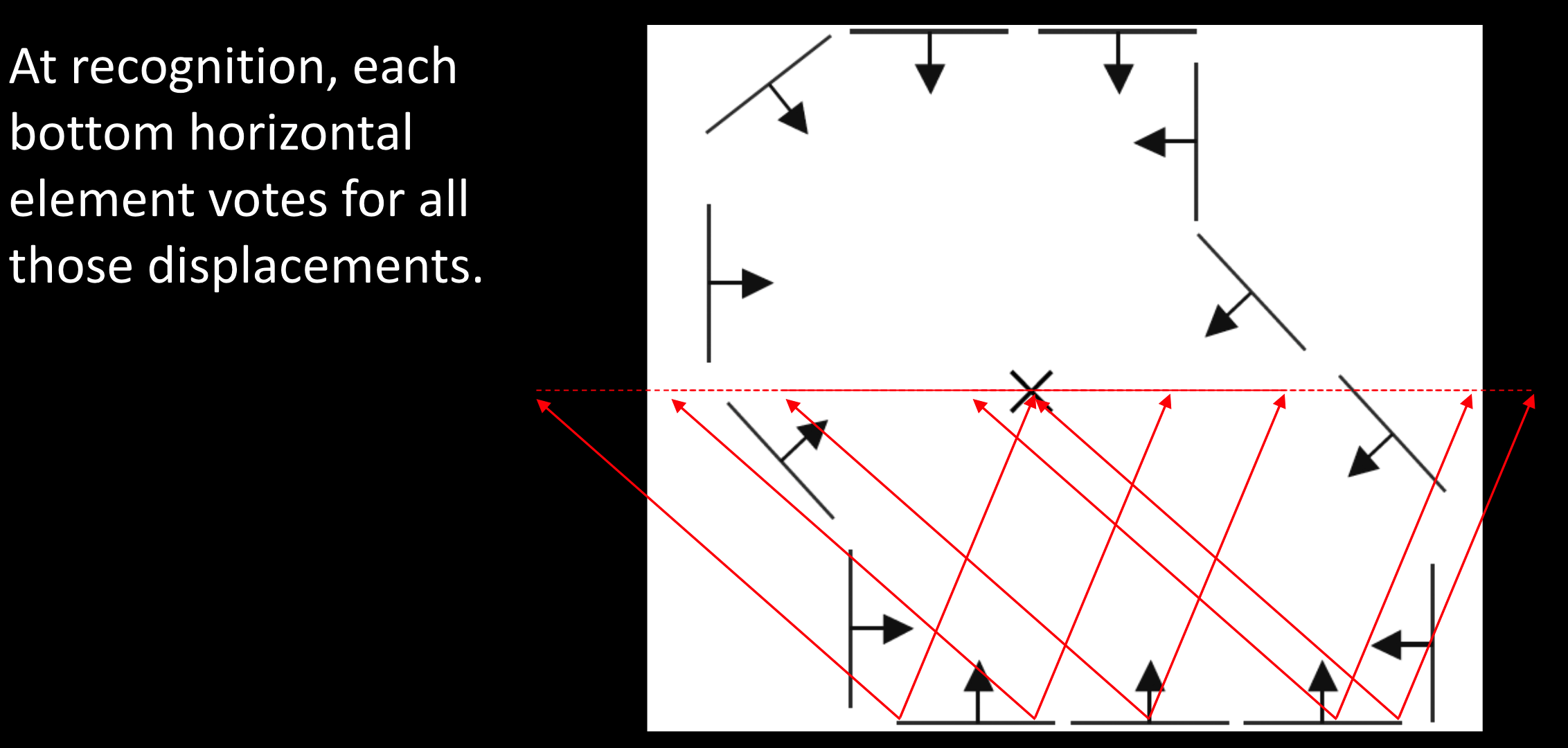
当下这个像素点的位移图,来源于它相同$\theta$的投票,做了平移,他们公用一个索引点,最终底部的所有像素点投票得出了一条直线。
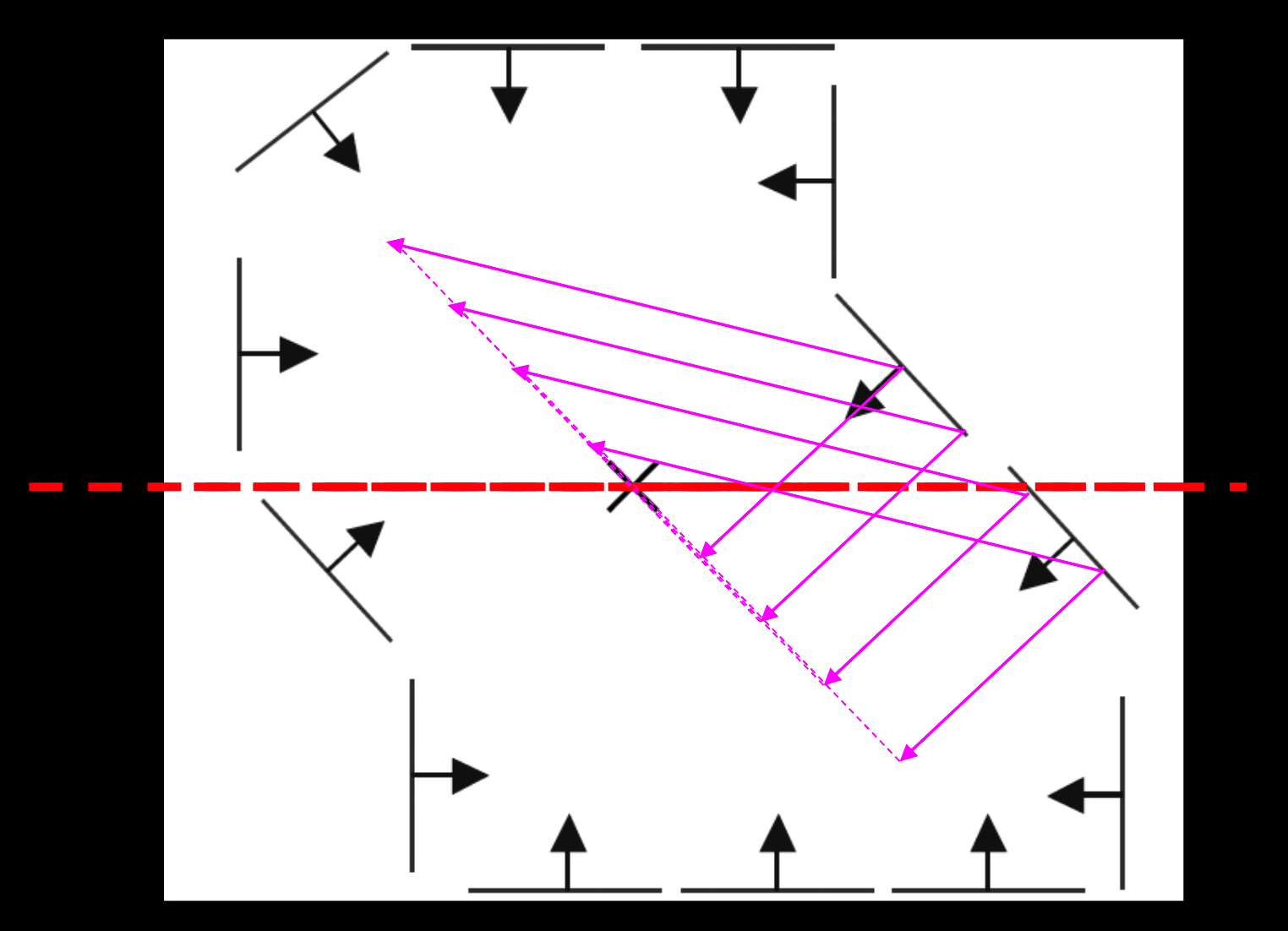
这条直线中,中心的投票数是最多的,通过对另一条边做相同操作,交点为中心点。
算法:默认不知道方向

不知道比例:
识别中的应用
基于视觉代码的索引:
生成代码块:
像素按蔟分类
生成特征:
生成位移投票:
在投票箱中,相同特征的投票数量就是特征的个数。
看轮胎投了几票
傅里叶变换
计算视觉将图像视为数据,而不是信号,但频率分析的思想很有用。
basis sets:标准基(线代的定义)
应用到图像的标准基:
把图像视为非常大的空间中的点,例如一个N*N的图像,可以认为是一个一维的向量。
另一种做法:
- 同一位置的图像:类似正弦余弦
上面就是傅里叶基,递增的是频率
正弦和
公式:$A\sin(\omega x^2+\varphi^2)$
共有三个自由度:
- $A$:幅度
- $\omega$:频率
- $\varphi$:相位
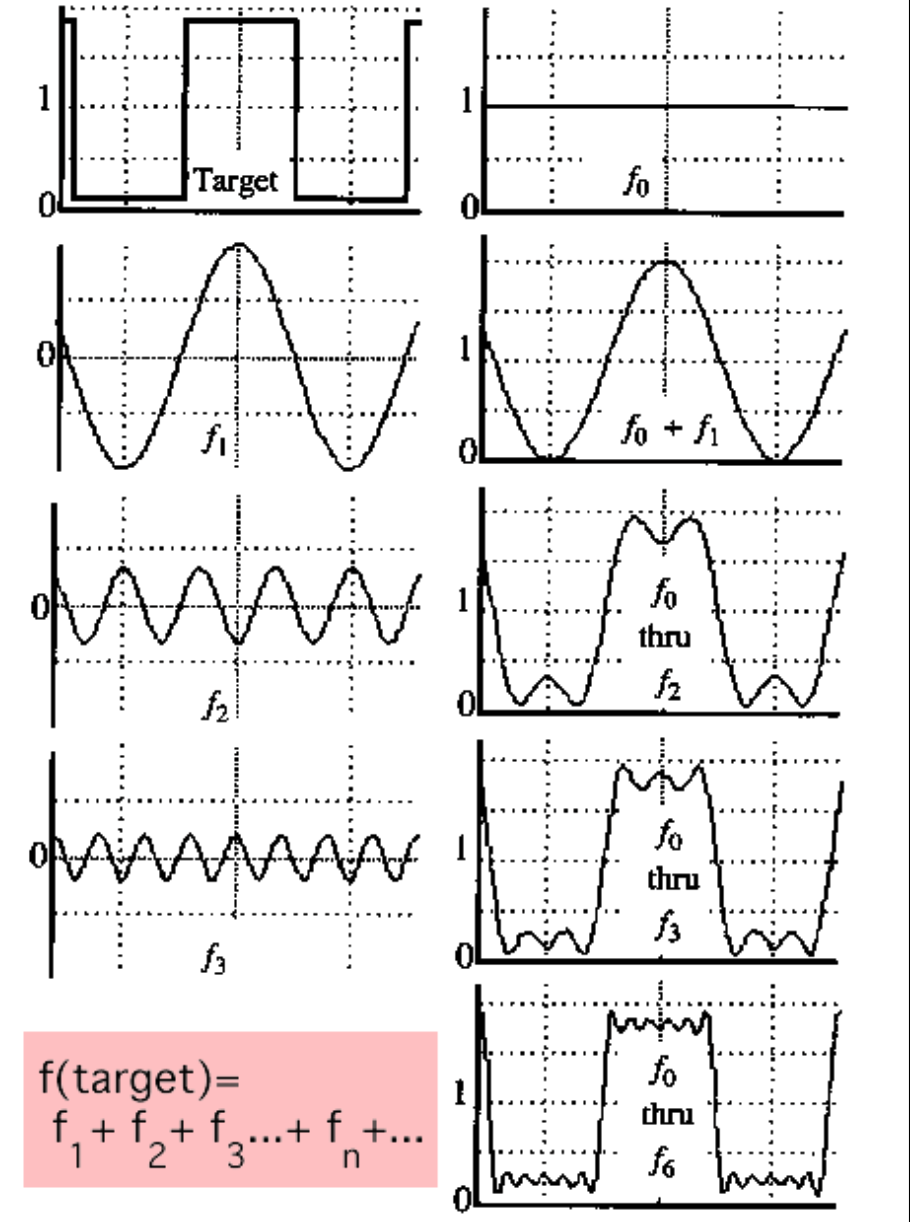
频率是最重要的,频率越高,摆动速度越快
时间和频率
$g(t)=\sin(2\pi ft)+\frac13\sin(2\pi(3f)t)$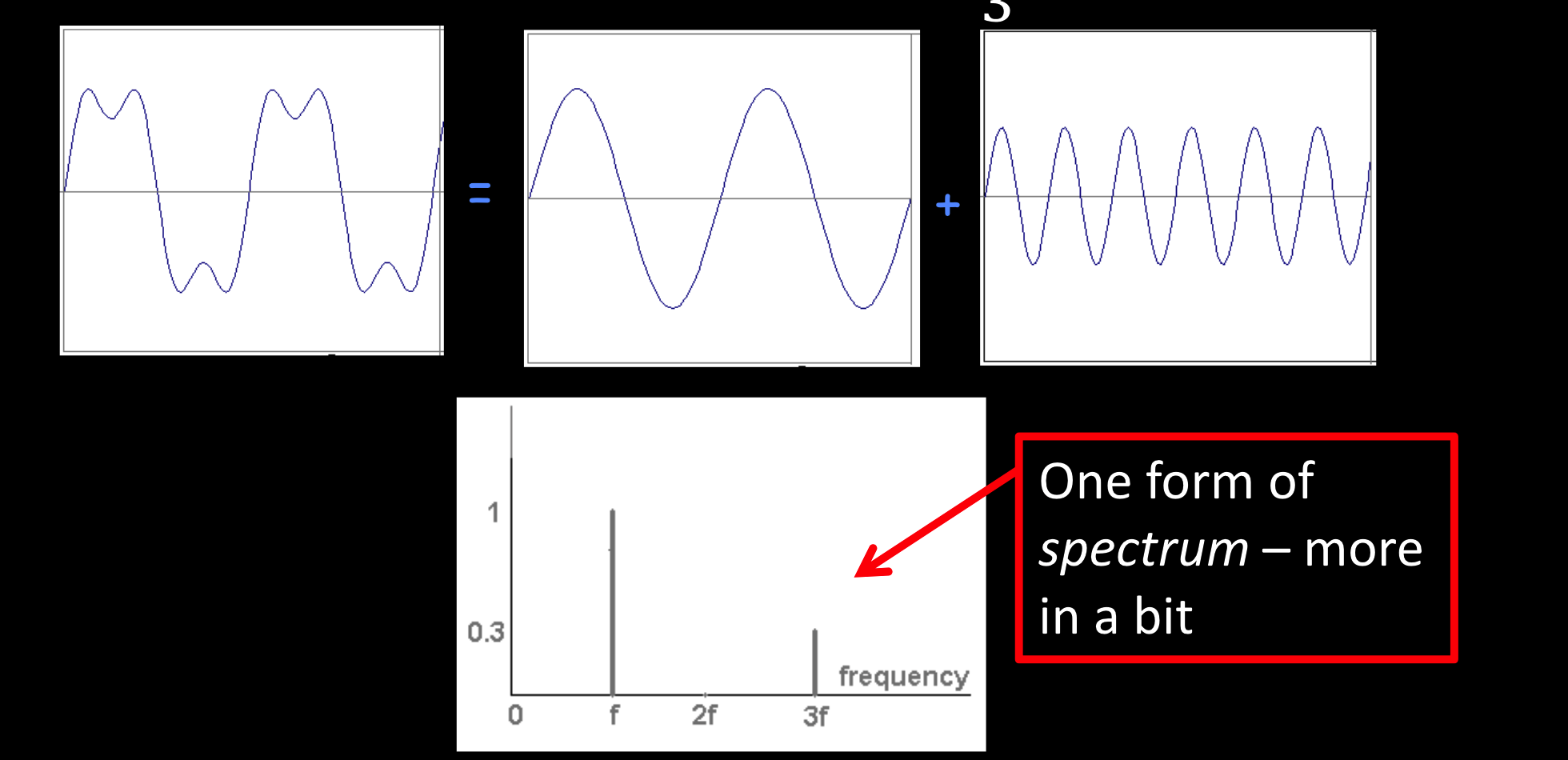
一种绘制光谱的方式
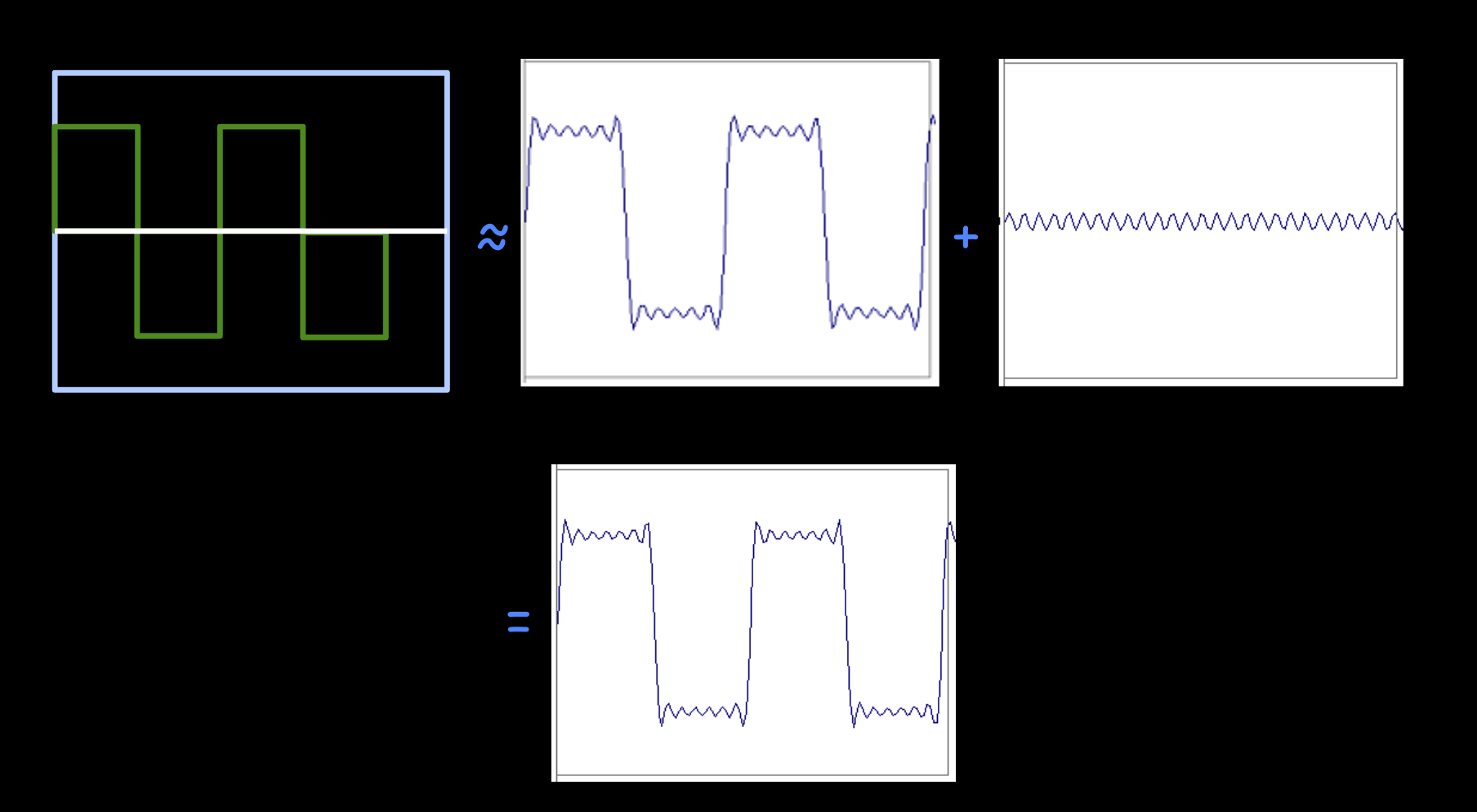
f越大,越接近方波
方波的正弦公式:$A\sum\limits_{k=1}^{\infty}\frac{1}{k}\sin\left(2\pi kt\right)$
图像: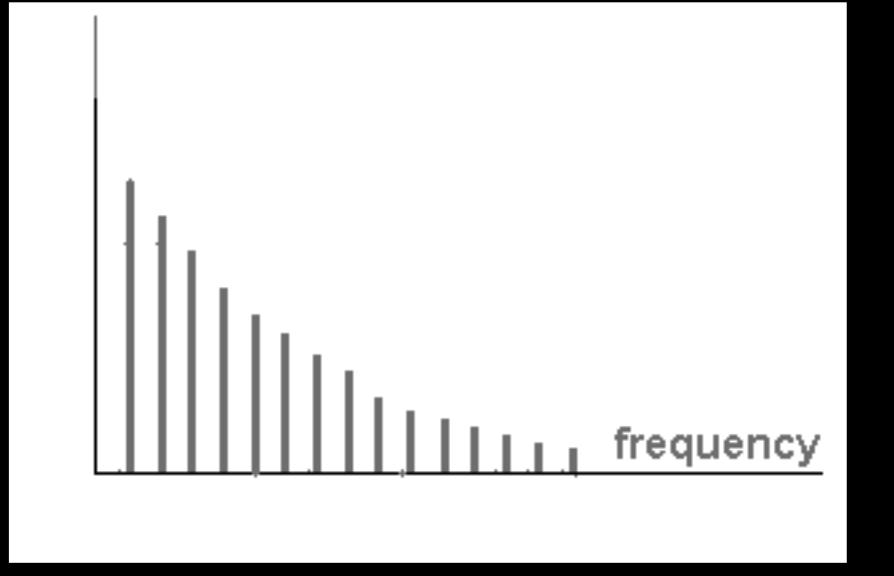
不考虑相位
傅里叶变换
$f(x)\longrightarrow\boxed{\begin{array}{c}\text{Fourier}\\\text{Transform}\end{array}}\longrightarrow F(\omega)$
复数:$\begin{aligned}F\left(\omega\right)&=R\left(\omega\right)+iI\left(\omega\right)\end{aligned}$
性质:
- $A = \pm\sqrt{R \left( \omega \right)^2 + I \left( \omega \right)^2}$
- $\varphi^2=\tan^{-1}\frac{I\left(\omega\right)}{R\left(\omega\right)}$
虚部是奇函数-正弦,实部是偶函数-余弦。
计算傅里叶变换
基本性质:
$\int_{-\infty}^\infty\sin(ax+\phi)\sin(bx+\varphi)dx=0,\mathrm{~if~}a\neq b$
$\int_{-\infty}^\infty\sin(\alpha x+\phi)\sin(\alpha x+\varphi)dx=\pm\infty$
例子:
假设一个展开为余弦的函数:
$f\left(x\right)=\cos\left(2\pi\omega x\right)$
$C\left(u\right)=\int_{-\infty}^{\infty}f\left(x\right)\cos\left(2\pi ux\right)dx$
- 如果$u == \omega$:积分为无穷
- 如果$u \neq \omega$:积分为0
得到脉冲图: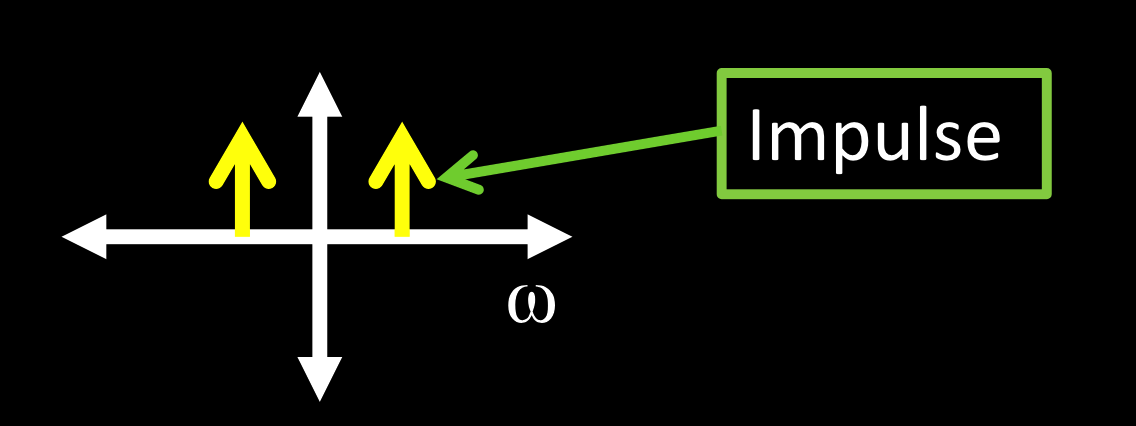
被称作与余弦对应的脉冲
如果是正弦,左边将会是负的脉冲:$\sin(-x) = -\sin(x)$
傅里叶变换通用定义
定义:$F\left(u^2\right)=\int_{-\infty}^{\infty}f\left(x^2\right)e^{-i2\pi ux}dx$
其中:$e^{ik}=\text{ cos }k+i\sin k\quad i=\sqrt{-1}$
作用:从空间域转换到频域
傅里叶逆变换:$f\left(x\right)=\int_{-\infty}^\infty F\left(u\right)e^{i2\pi ux}du$
可以恢复信号
频谱
常用频谱: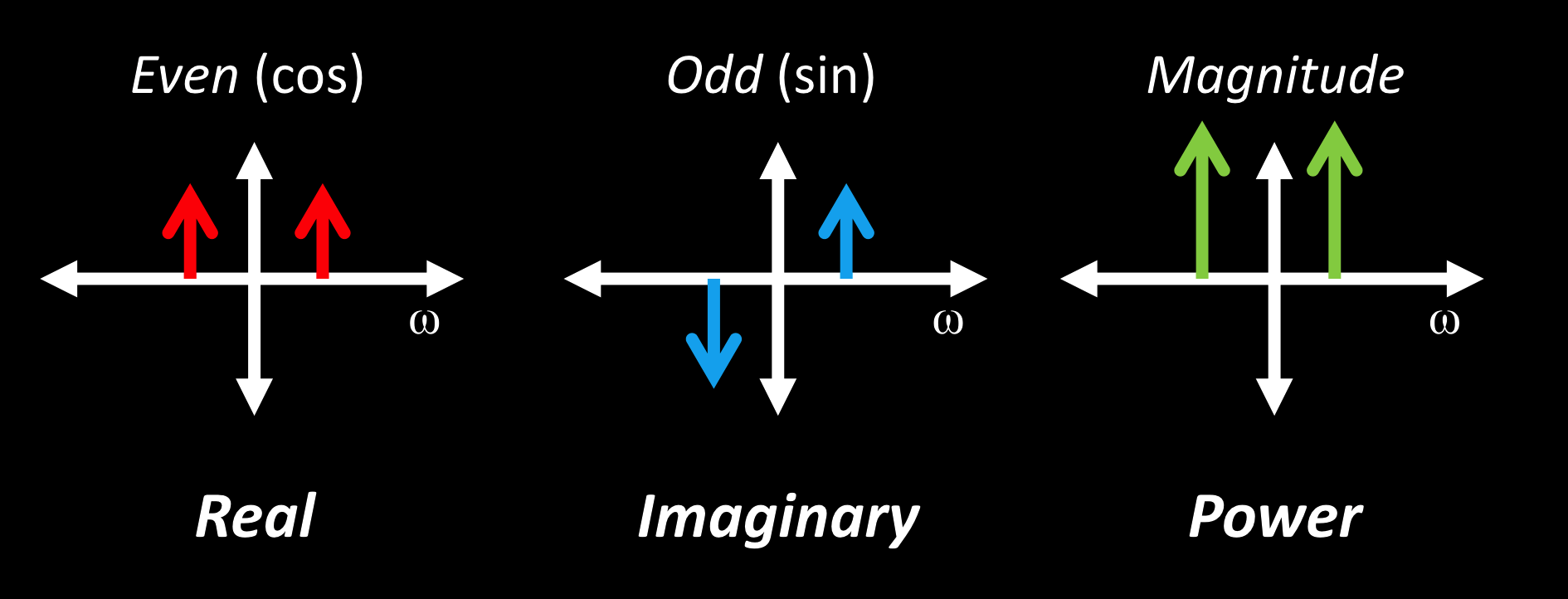
最后一个是幂频谱
频谱图: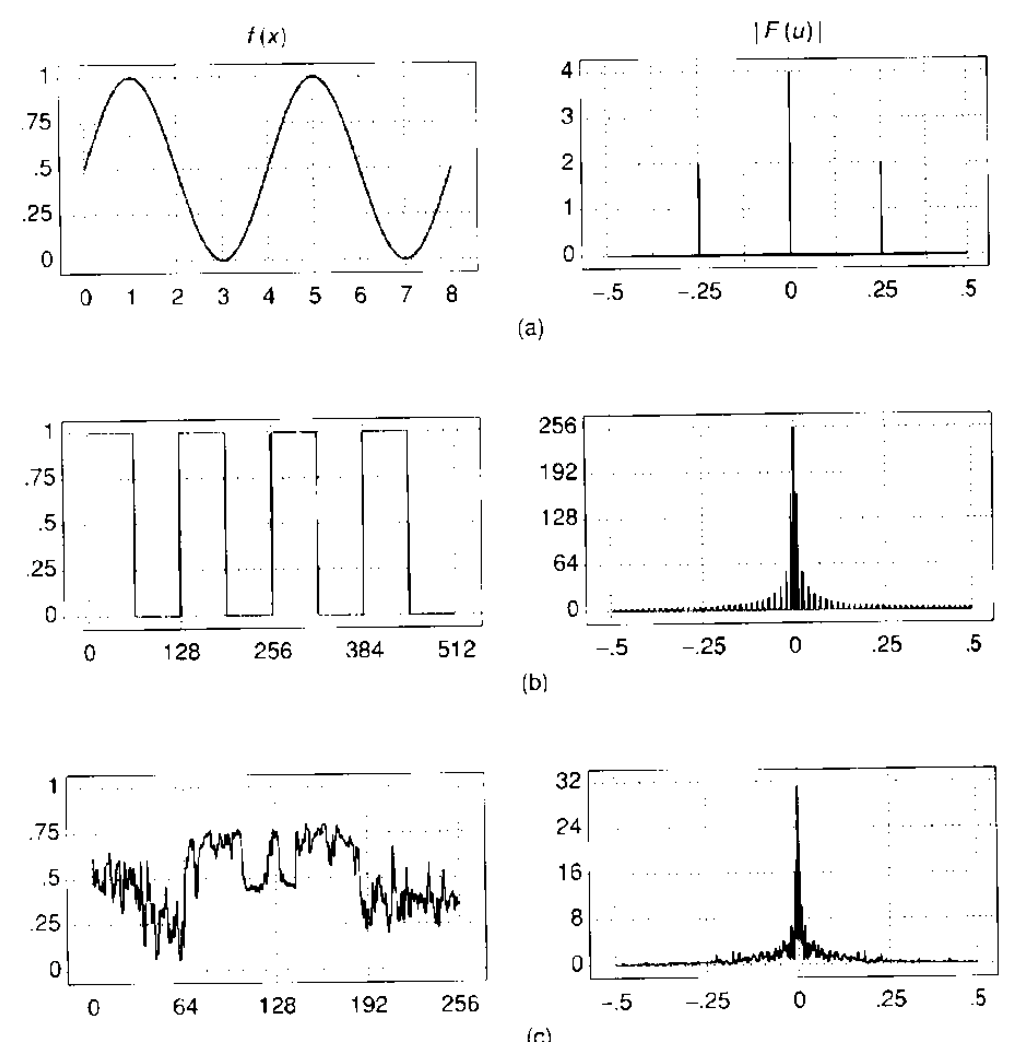
局限性:
傅里叶级数积分有界
傅里叶变换到傅里叶级数
级数:$F\left(k\right)=\frac1N\sum_{x=0}^{x=N-1}f\left(x\right)e^{-i\frac{2\pi kx}N}$
积分的另一种写法:离散化
二维的傅里叶
$F\left(u,\nu\right)=\int_{-\infty}^\infty\int_{-\infty}^\infty f\left(x,y\right)e^{-i2\pi\left(ux+\nu y\right)}dxdy\frac12$
离散:$F\left(k_x,k_y\right)=\frac1N\sum_{x=0}^{x=N-1}\sum_{y=0}^{y=N-1}f\left(x,y\right)e^{-i\frac{2\pi\left(k_xx+k_yy\right)}N}$
例子:
一个正弦曲线,处于特定的频率, 仅仅有垂直线组成: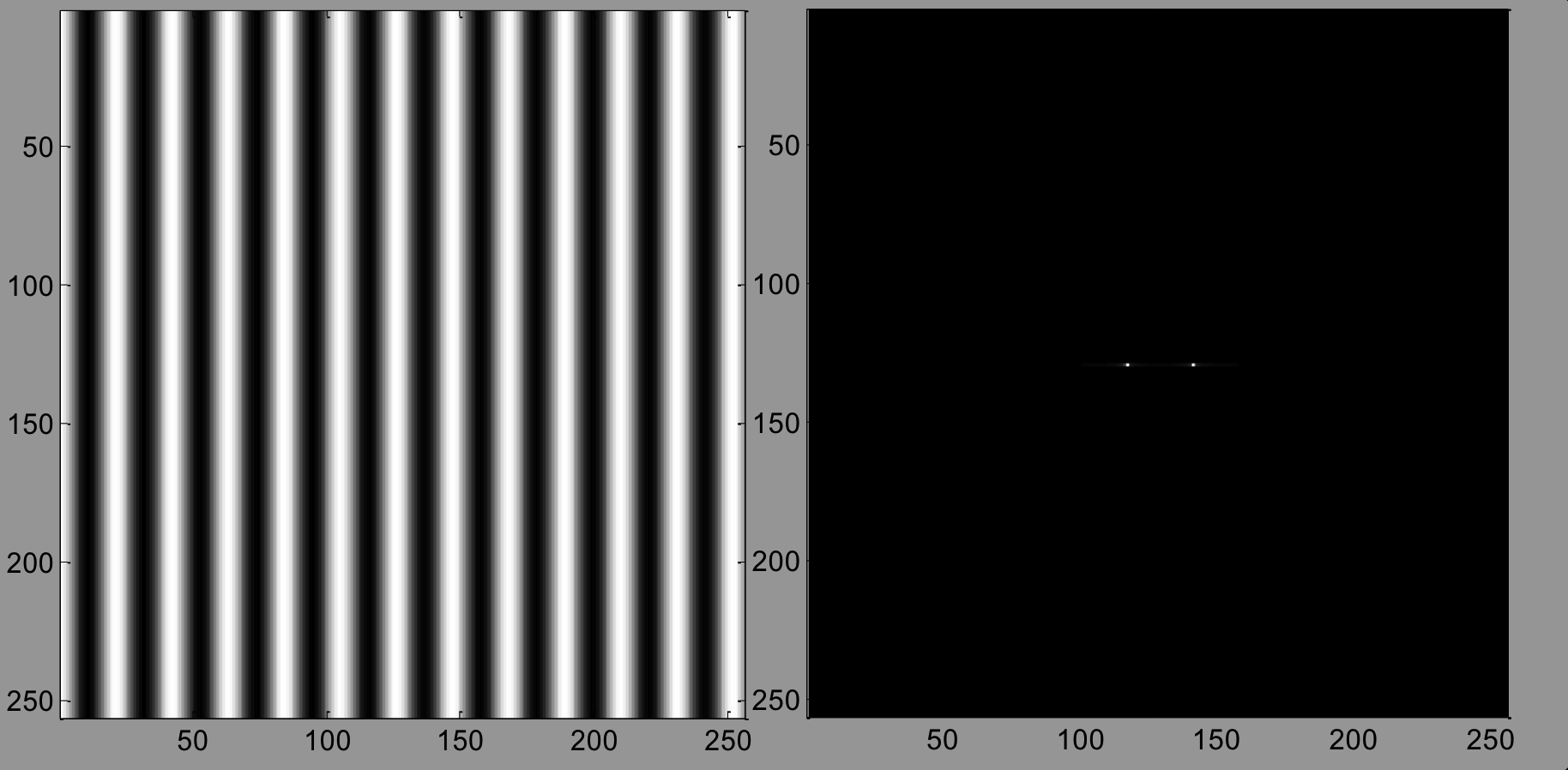
右图是它的傅里叶频谱和功能谱。
亮点就是频率的尖峰
一个余弦曲线,频率更快: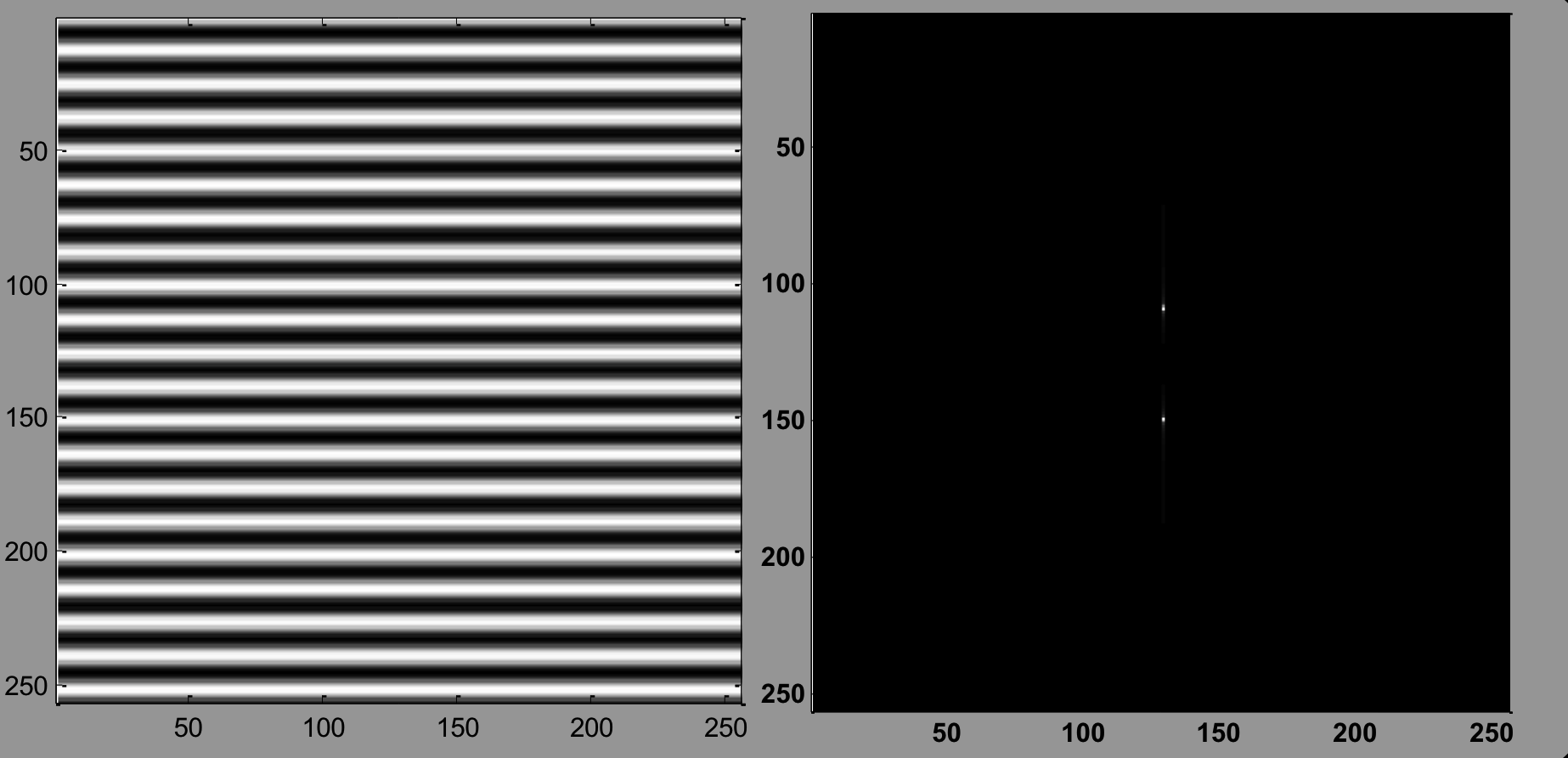
频率分量更高,峰值靠外
线性:傅里叶变换是一个线性变换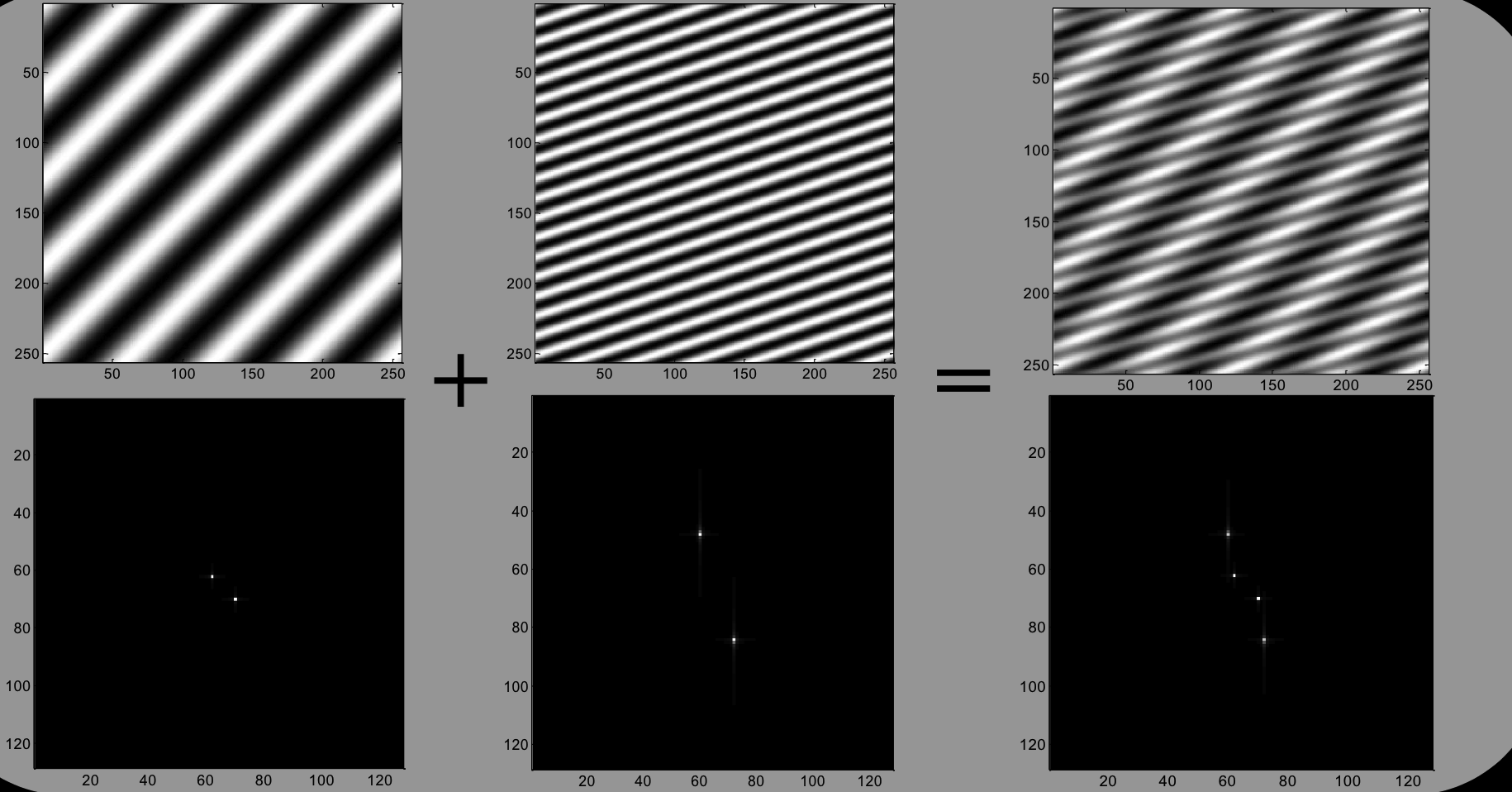
真实图像的光谱

自然图像有相同的光谱
重建图像才需要相位
用部分光谱重建图像,图像的变化如右图
高频率:告诉边缘在哪里,高频越亮,越清晰
明亮线垂直于轮廓线

人造场景:

思考:
- 如果不是周期函数,光谱会有倾斜
频率分析中的卷积
傅里叶变换与卷积
卷积:$g = f * h$
傅里叶变换:
\begin{split}
G\left(u\right)&=\int_{-\infty}^{\infty}g\left(x\right)e^{-i2\pi ux}dx \\
&=\int_{-\infty}^\infty\int_{-\infty}^\infty f\left(\tau\right)h\left(x-\tau\right)e^{-i2\pi ux}d\tau dx \\
&=\int_{-\infty}^\infty\int_{-\infty}^\infty\left[f\left(\tau\right)e^{-i2\pi u\tau}d\tau\right]\left[h\left(x-\tau\right)e^{-i2\pi u\left(x-\tau\right)}dx\right] \\
&=\int_{-\infty}^{\infty}\left[f\left(\tau\right)e^{-i2\pi u\tau}d\tau\right]\int_{-\infty}^{\infty}\left[h\left(x^{\prime}\right)e^{-i2\pi ux^{\prime}}dx^{\prime}\right] \\
&=F\left(\begin{array}{c}u\\\end{array}\right)H\left(\begin{array}{c}u\\\end{array}\right)
\end{split}
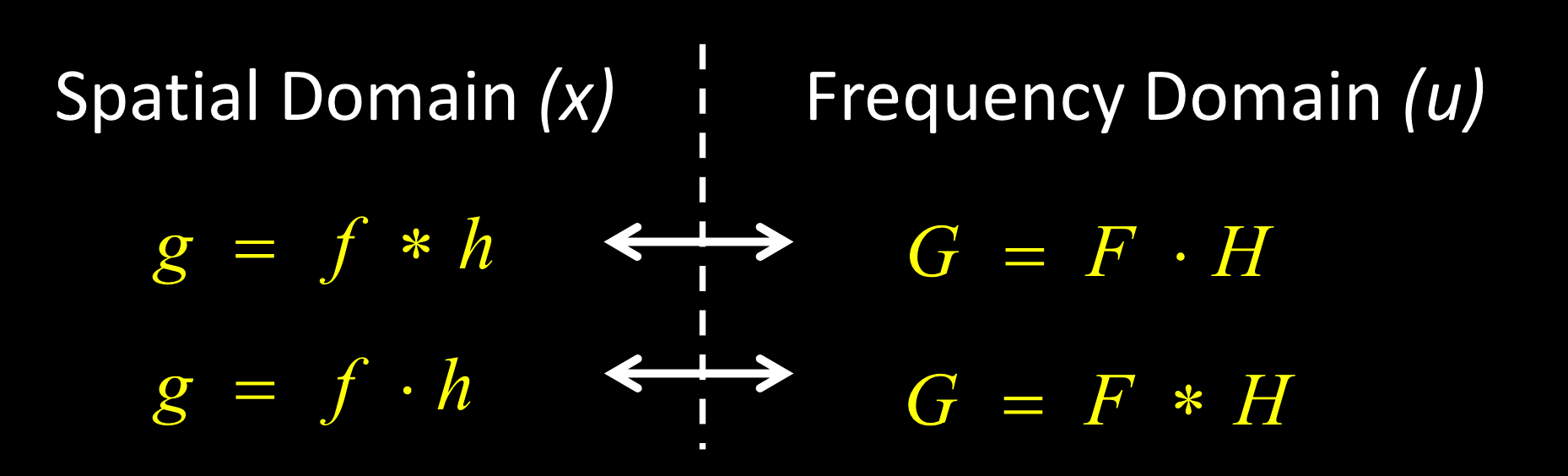
空间中乘积$\Leftrightarrow$频率空间中卷积
大掩码的空间域卷积很复杂,用快速傅里叶变换可以转换为频率域乘法,避免卷积。
平滑和模糊中的应用
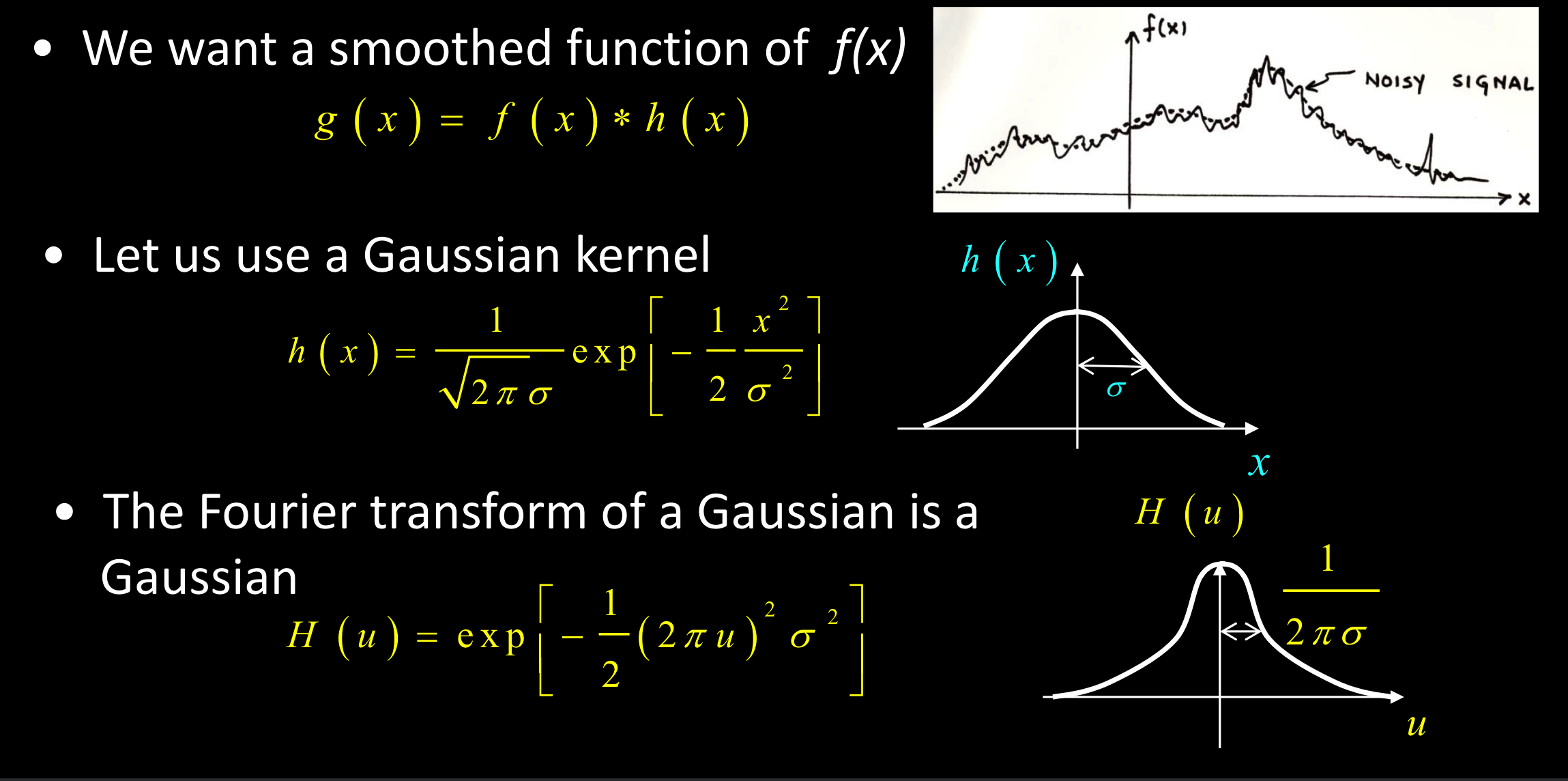

瘦高斯的傅里叶是胖的
原因:
如果高斯很瘦,就希望保留所有的频率,傅里叶就很胖。
高斯很胖,模糊了一切,就只保留一点点低频率,几乎没有高频率。
作用:
保存低频率,降低高频率。
空间采样频率越低,傅里叶频率越高.
傅里叶的放缩原理
效果图;
傅里叶变换的性质
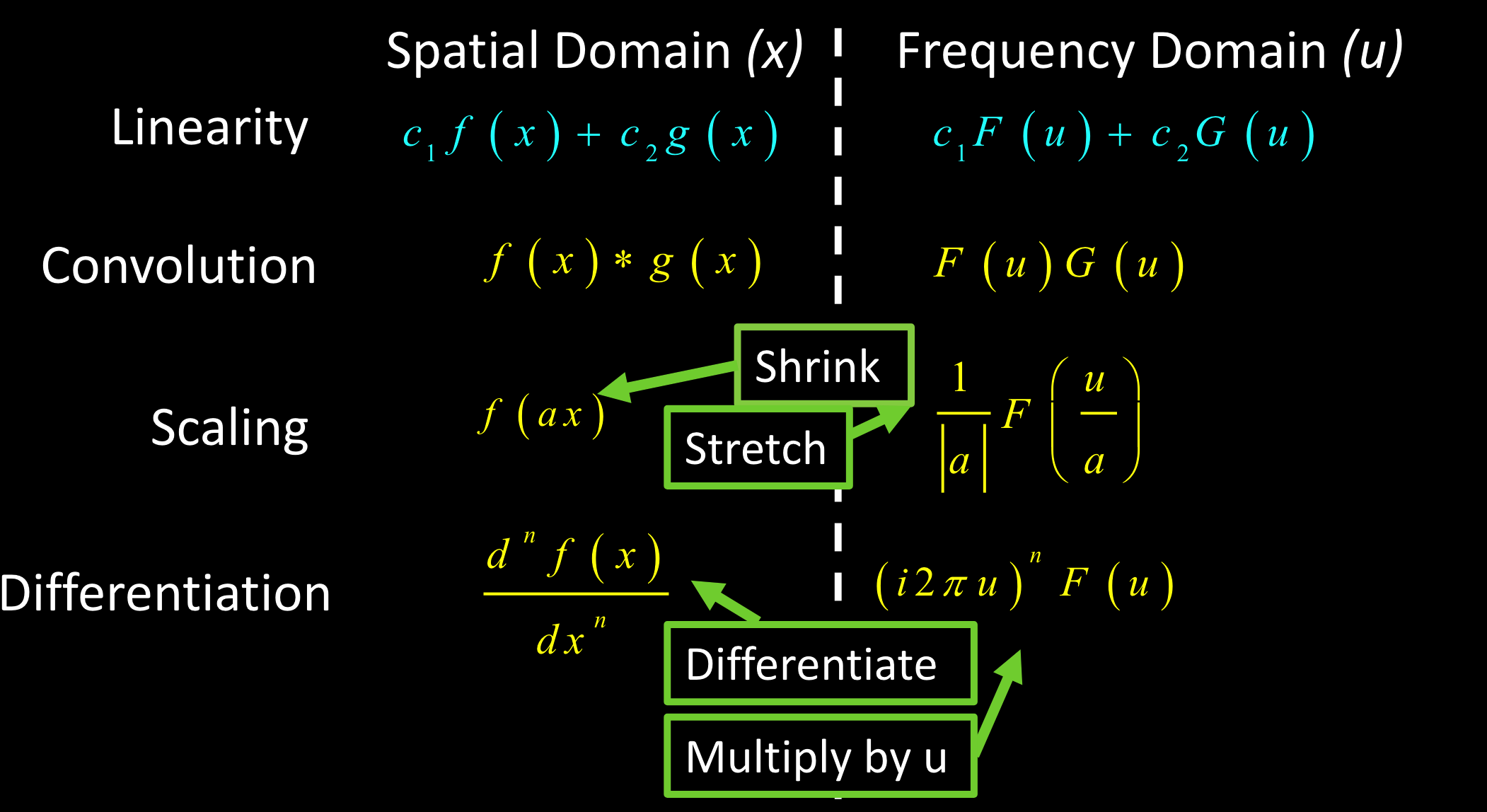
傅里叶对: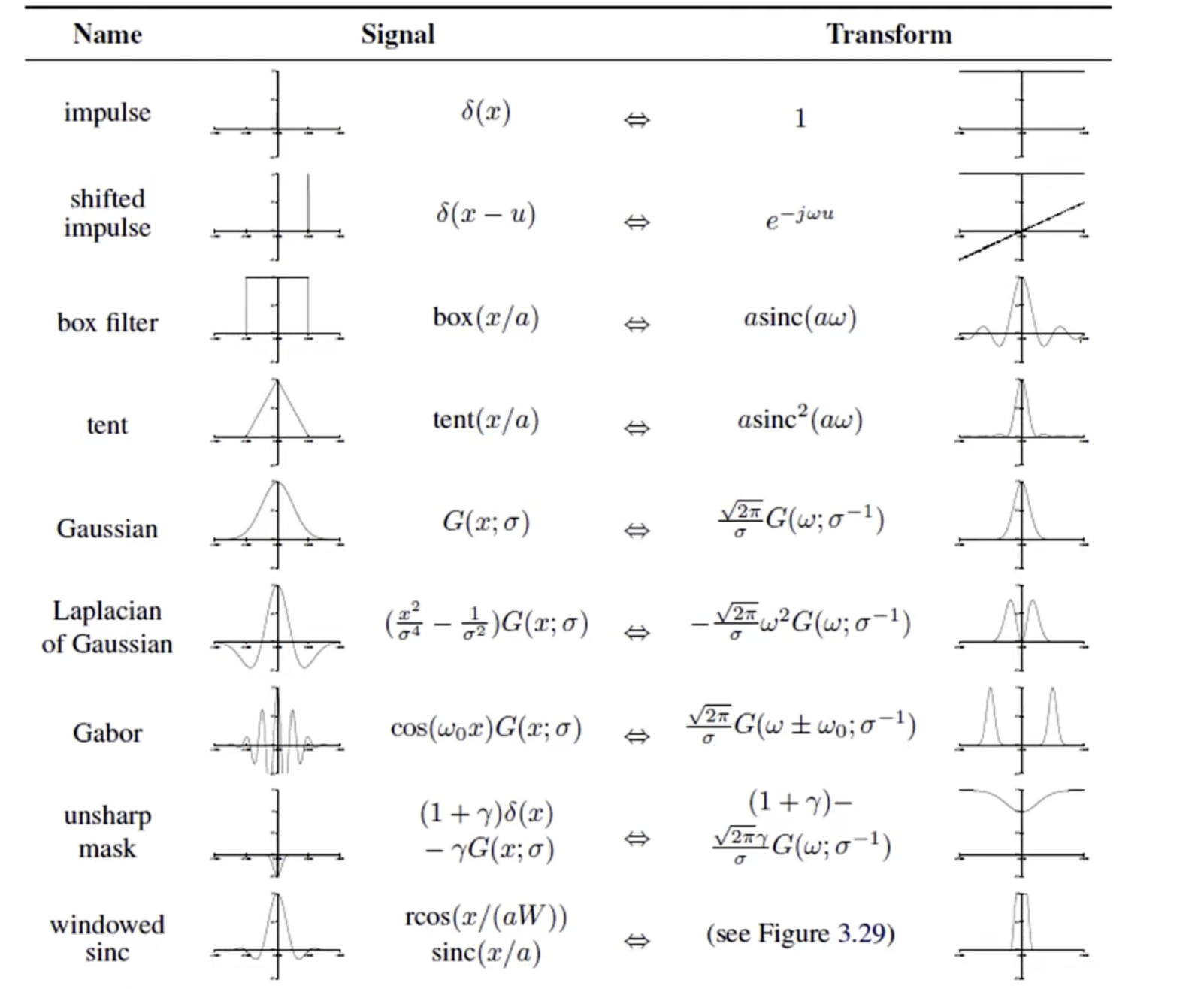
混叠 Aliasing
傅里叶基是如何混叠的?
脉冲串的概念
脉冲串的傅里叶变换是另一个脉冲串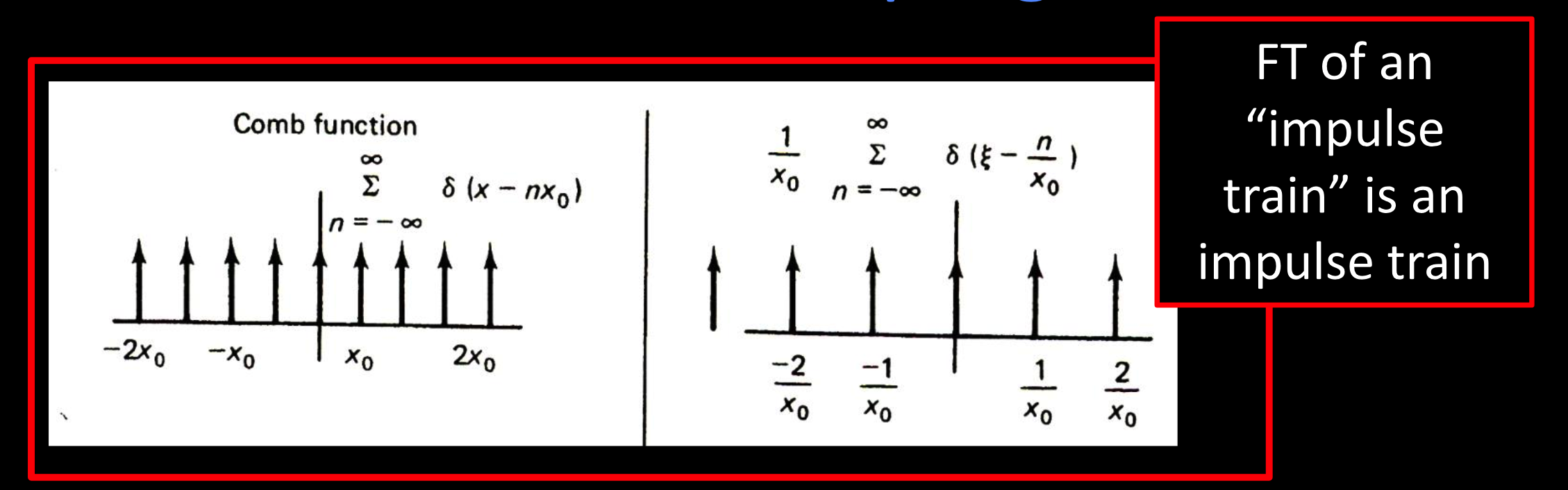
空间中脉冲距离越远,频率中脉冲越接近
采样和重构
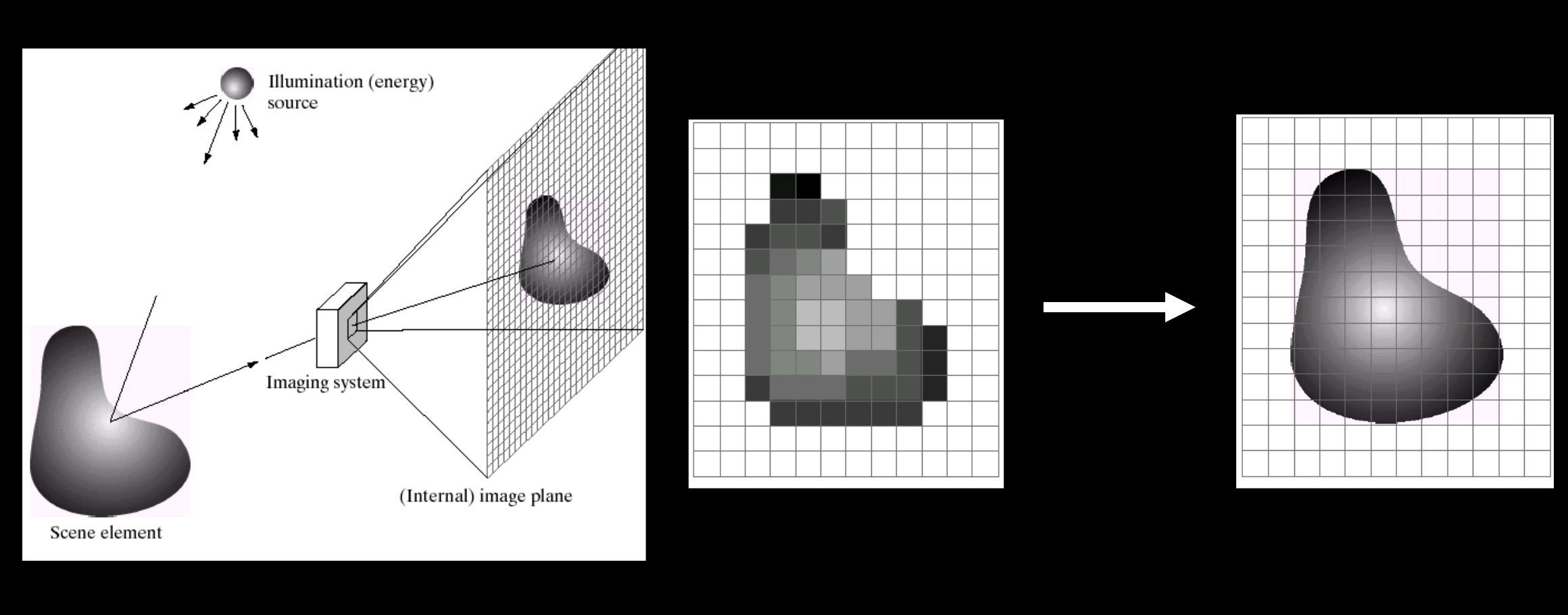
采样是计算机如何存储连续信号提出的,如何重建原始信号?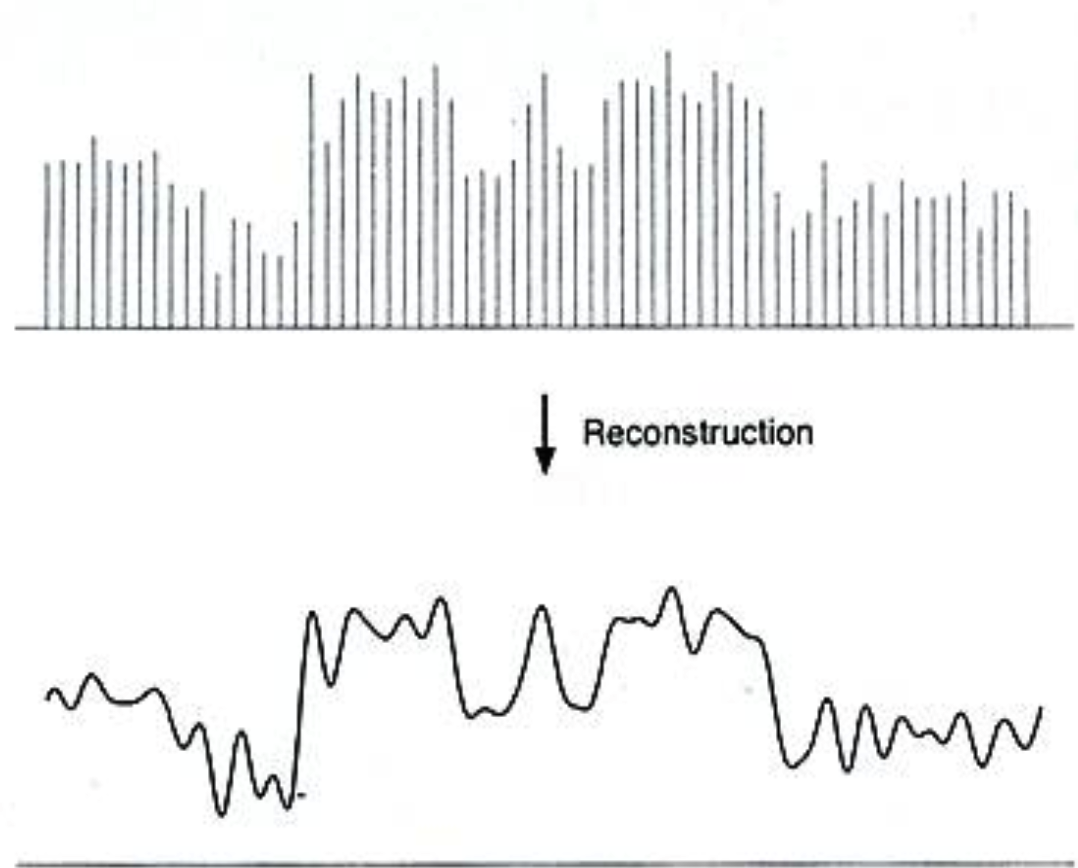
在离散位置如何将信号连续起来。
样例: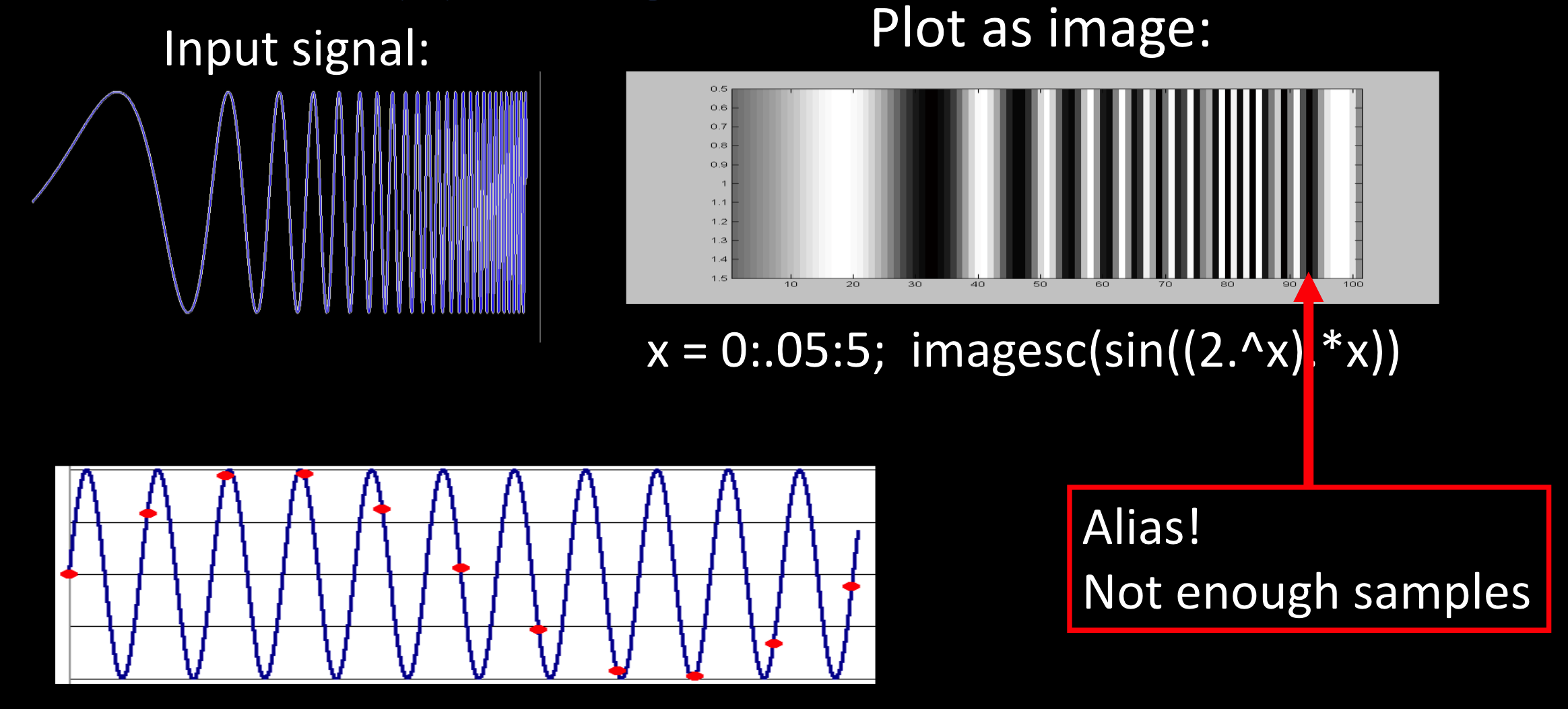
采样密度不够,无法恢复图像。
如何防止锯齿出现?
过滤高频率,降低采样量。
脉冲
一维脉冲函数:$comb_M[x]=\sum_{k=-\infty}^{\infty}\delta[x-kM]$
图像: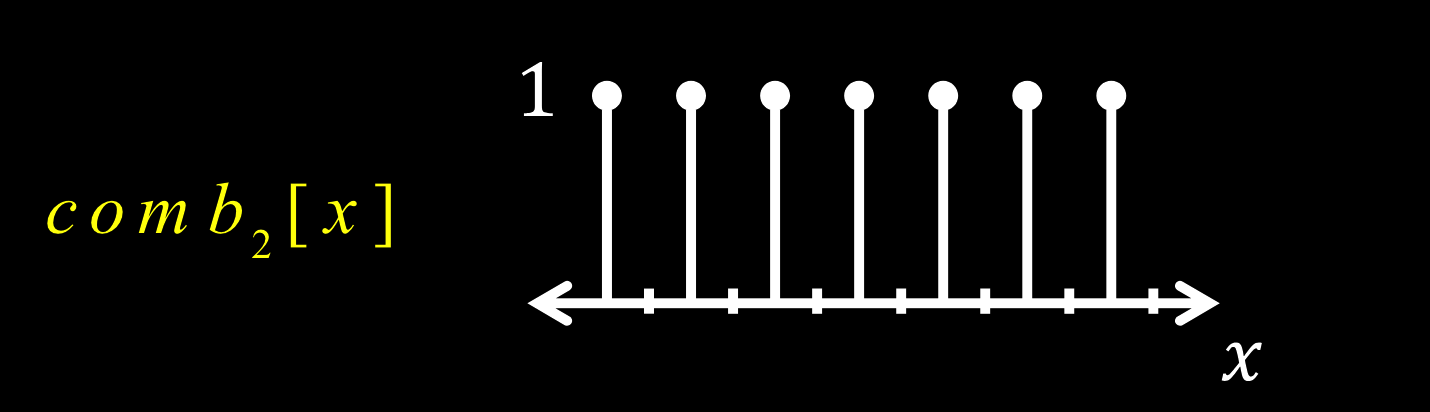
二维脉冲函数:$comb_{M,N}(x,y)\equiv\sum_{k=-\infty}^\infty\sum_{l=-\infty}^\infty\delta\left(x-kM,y-lN\right)$
傅里叶变换:
$\sum_{k=-\infty}^n\sum_{l=-\infty}^n\delta\left(x-kM,y-lN\right)\Leftrightarrow\frac1{MN}\sum_{k=-\infty}^\infty\sum_{l=-\infty}^\infty\delta\left(u-\frac kM,\nu-\frac lN\right)$
采样低频信号
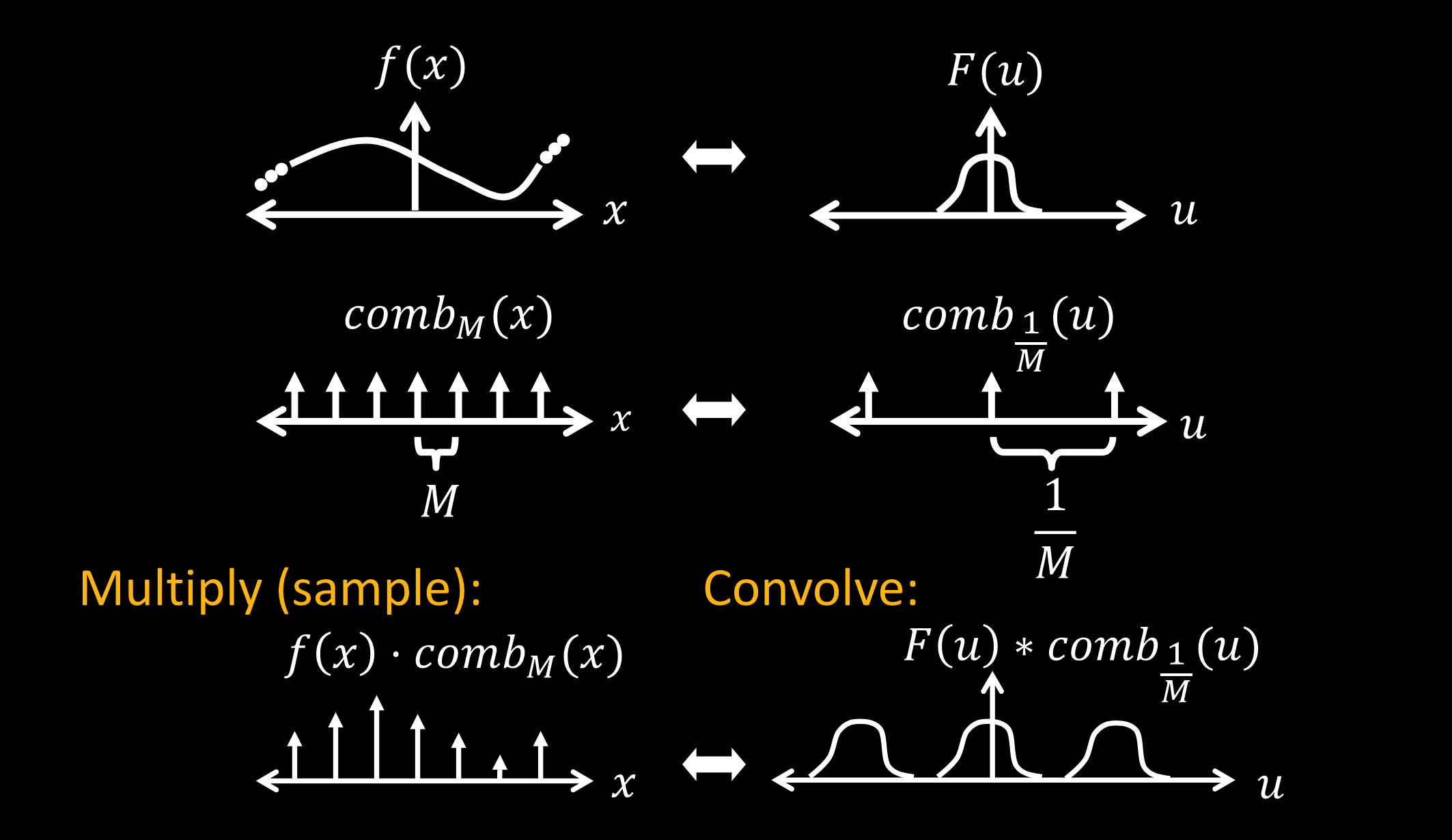
采样:连续信号乘离散梳函数
如果功能频率$W$满足:$W<\frac1{2M}$,就可以恢复。
这里有一些采样定理的内容
采样高频信号
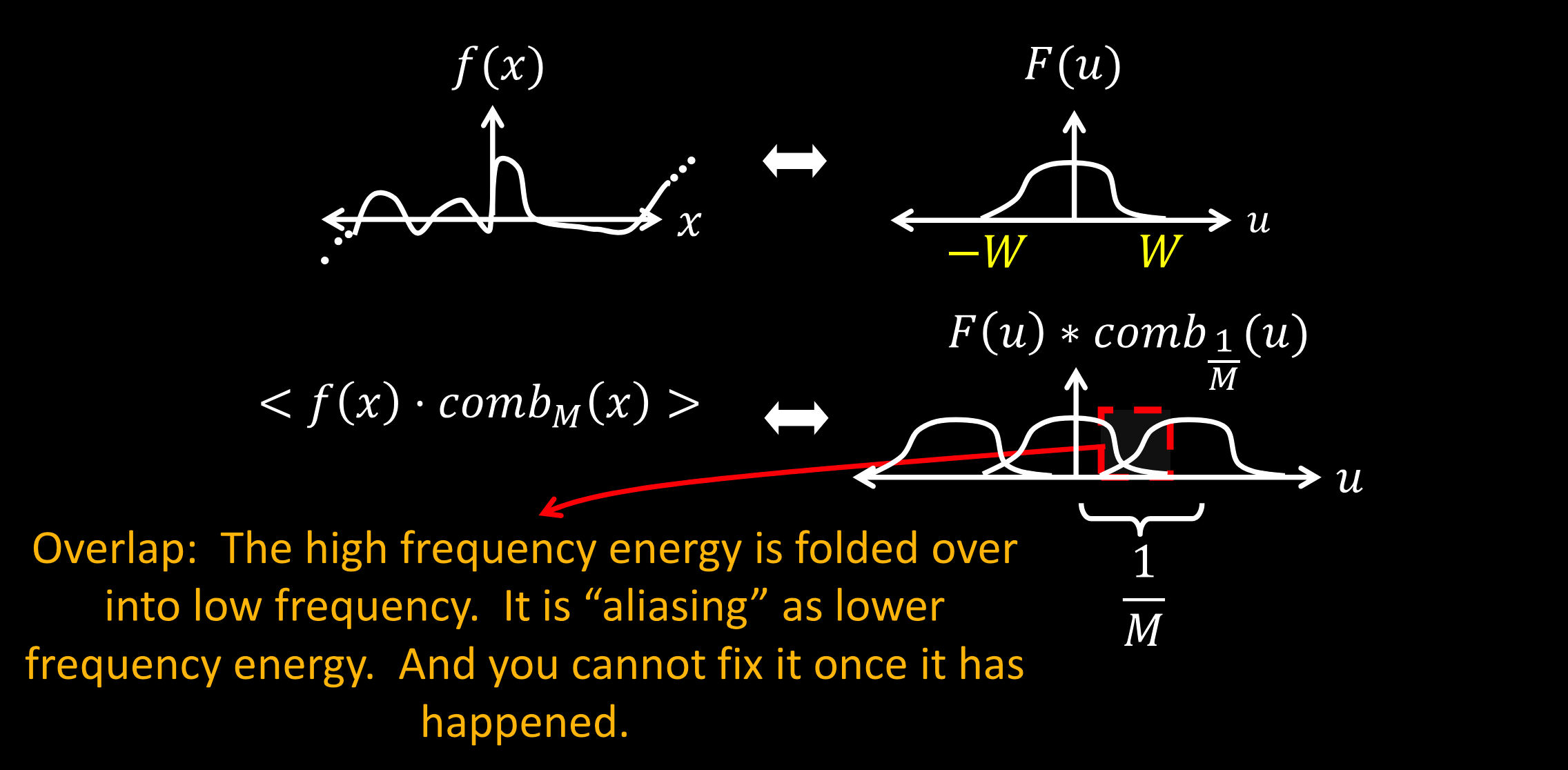
高频信号采样重叠了,采样之前,必须去处高频,以防重叠。
如何去处高频?
梳状滤波器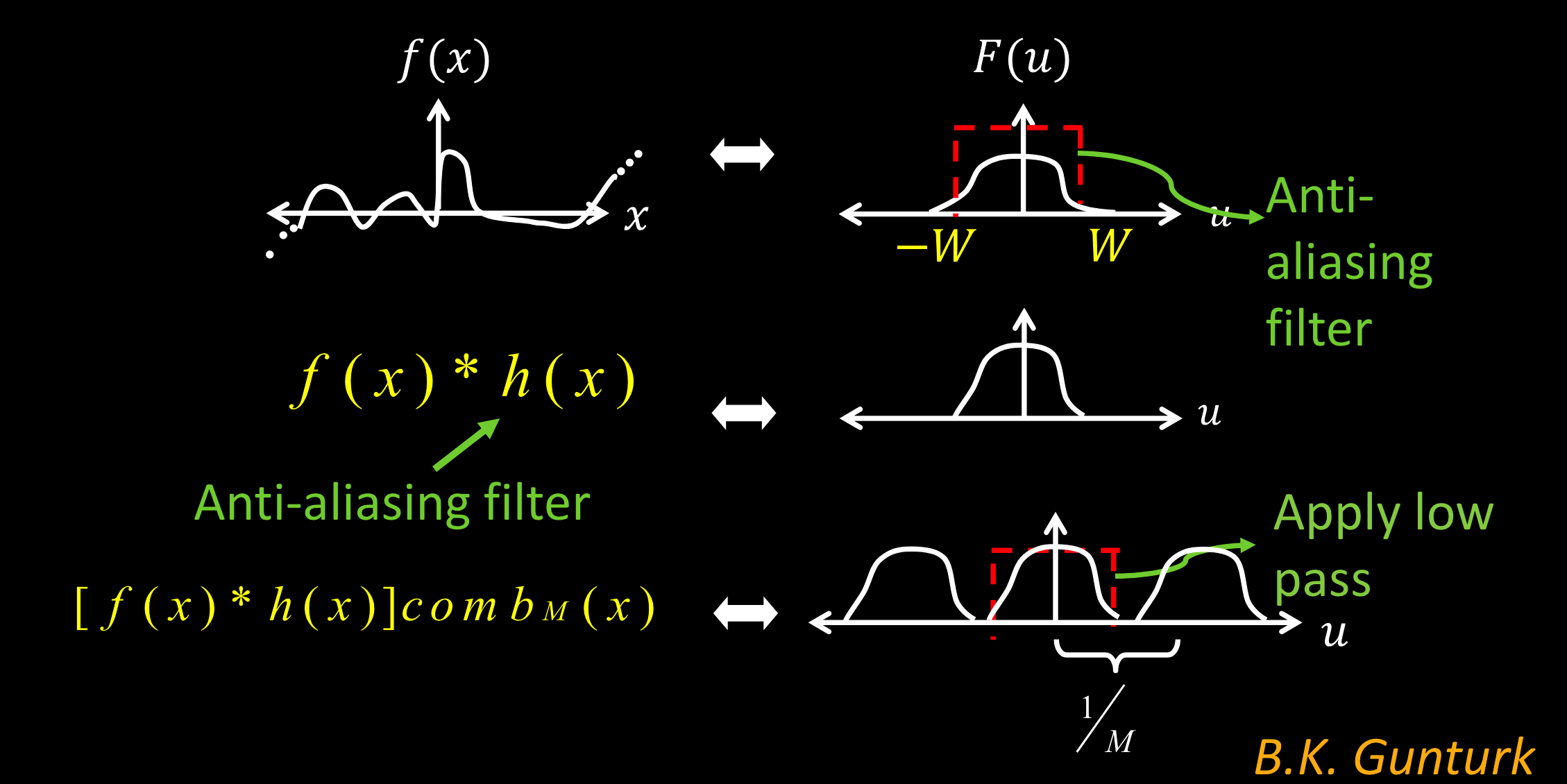
图像中的重叠
图像缩小,如果直接丢掉行列,图像会变小。放大图像后,图像不像是缩小的图像,很模糊。
正确的做法是:用高斯滤波。
高斯滤波做了抗锯齿,所以效果更好。
对比度敏感
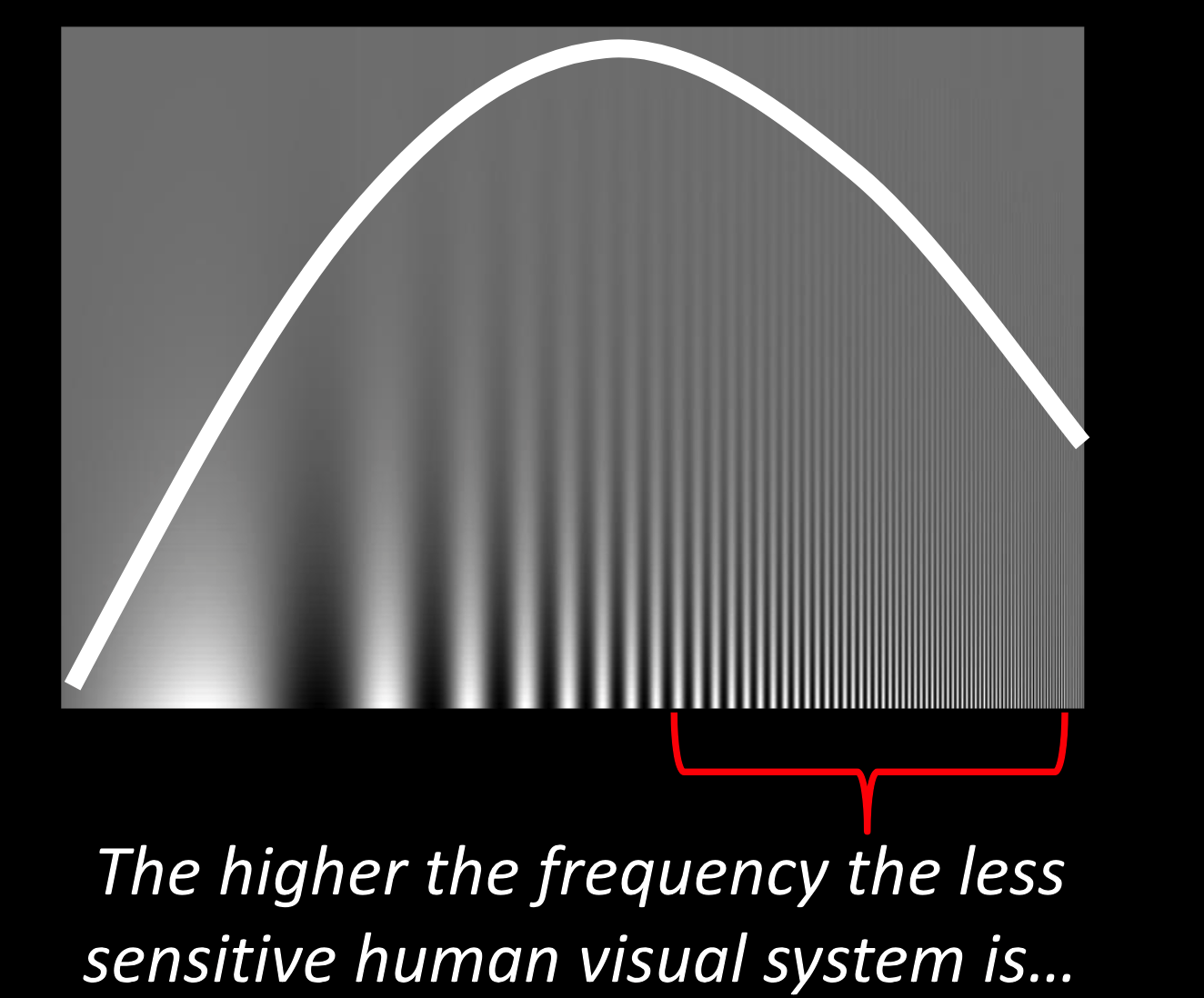
人类的视觉对高频不敏感。
JPEG
DCT:离散余弦变换
不保留高频信息,降低图像质量时,只保存低频率信息。