14-数值稳定性+模型初始化和激活函数
更新历史
- 24.04.24:初稿
系列
14-数值稳定性+模型初始化和激活函数
1. 数值稳定性
数值稳定性是深度学习中比较重要的点,特别是当神经网络变得很深的时候,数值通常很容易变得不稳定。
1.1 神经网络的梯度

考虑d层神经网络
t表示层数,$h^{t-1}$表示第t-1层的输出,经过一个$f_{t}$函数后,得到第t层的输出。
最终输出y的表示:输入x经过若干层(d层)的函数作用,最后被损失函数作用得到输出y。
计算损失函数L关于第t层参数$W_{t}$的梯度
由链导法则得到上图中乘积公式
需要进行d-t次矩阵乘法(为什么是矩阵乘法?答:由于所有的h都是一些向量,导数中分子分母均为向量,所以求导得到的是矩阵,维数为[分子维度]x[分母维度],可以参考第6节视频和笔记)。这也是导致数值稳定性问题的主要因素,由于做了太多次的矩阵乘法。
1.2 数值稳定性的常见两个问题
梯度爆炸
假设梯度都是一些比1大的数比如1.5,做100次乘积之后得到$4\times 10^{17}$,这个数字很容易带来一些浮点数上限的问题(需了解更多请参考计算机系统-计算机中浮点数的存储方式)。
梯度消失
假设梯度都是一些比1小的数比如0.8,做100次乘积之后得到$2\times10^{-10}$,也可能会带来浮点数下溢的问题。
1.3 例子:MLP
此处我们着重探讨1.1节中所述的求梯度时所做的d-t次矩阵乘法,并以一个实例MLP来探讨其结果的具体形式。

第一行公式,定义$h^{t}$和$h^{t-1}$(均为向量)的函数关系$f_{t}$,第t层的权重矩阵作用于t-1层的输出$h^{t-1}$后经过激活函数$\sigma$得到$h^{t}$,注意激活函数$\sigma$逐元素计算。
第二行公式:这里用到链导法则,激活函数$\sigma$先对内部向量逐元素求导,然后把求导后这个向量变成对角矩阵(可以理解为链导法则中内部向量$W_{t}h_{t-1}$对自身进行求导,变成一个nxn的对角矩阵,更多请参考邱锡鹏 《神经网络与深度学习》 图片1)

图片1. 引自邱锡鹏 《神经网络与深度学习》附录:数学基础 ↩
- 视频中勘误说明:链导法则中$\frac{\partial W^{t}h^{t-1}}{\partial h^{t-1}}= W^{t}$而不是$\left (W^{t} \right )^{T}$(这点由分子分母维度也容易推出),故最终求导结果包含$W^{t}$,而不是其转置。
1.3 梯度爆炸
1.3.1 使用ReLU作为激活函数

由于激活函数Relu求导后或者是1或者是0,变为对角矩阵的斜对角线元素后,与$W^{i}$做乘积,斜对角线为1的部分会使得W中元素保留,最终该连乘式中有一些元素来自$\prod\left ( W^{i} \right )$ ,如果大部分$W^{i}$中 值都大于1,且层数比较大,那么连乘之后可能导致梯度爆炸的问题。
1.3.2 梯度爆炸问题
值超出值域(infinity)
- 对于16位浮点数尤为严重(数值区间 [6e-5 , 6e4]),GPU用16位浮点数更快
对学习率敏感
如果学习率太大→大参数值→更大的梯度,如此循环几次,容易导致梯度爆炸
如果学习率太小→训练无进展
我们可能需要在训练过程中不断调整学习率
1.4 梯度消失
1.4.1 使用Sigmoid作为激活函数
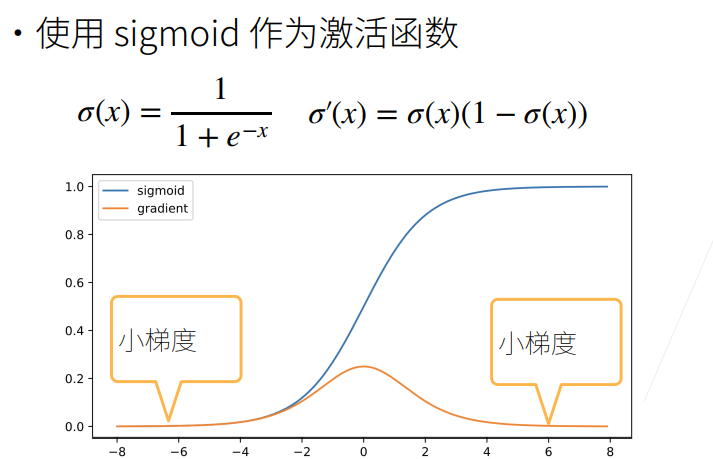
- 蓝色曲线为函数值
- 黄色曲线为梯度,注意到当输入x值取±6时,此时梯度已经变得很小,由图也可以看出,当输入值稍大或稍小都很容易引起小梯度。
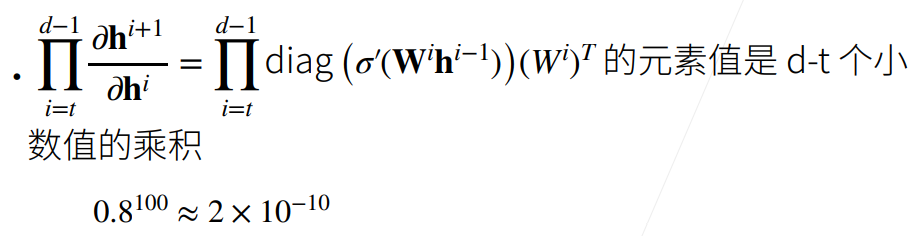
所以最终连乘式中$\prod diag\left ( \sigma ^{‘}\left ( W^{i}h^{i-1} \right ) \right )$项乘出来会很小,导致整个梯度很小,产生梯度消失问题。
1.4.2 梯度消失的问题
梯度值变为0
- 对16位浮点数尤为严重
训练没有进展
- 不管如何选择学习率,由于梯度已经为0了,学习率x梯度=0
- 对于底部层尤为严重
- 仅仅顶部层训练得较好。第t层导数包含d-t个矩阵乘积,越往底层走,t越小,乘得越多,梯度消失越严重,所以底部层效果更差。
- 无法让神经网络更深。只能把顶部层训练得比较好,底部层跑不动,这和给一个浅的神经网络没有什么区别。
2. 模型初始化和激活函数
2.1 让训练更加稳定
我们的一个核心目标是如何让训练更稳定,梯度值不要太大也不要太小
- 目标:让梯度值在合理的范围内
- 例如 [1e-6, 1e3]
常用方法:
- 将乘法变加法:
- ResNet(跳跃连接,如果很多层,加入加法进去)
- LSTM(引入记忆细胞,更新门,遗忘门,通过门权重求和,控制下一步是否更新)
归一化:
梯度归一化(归一化均值,方差)
梯度裁剪(clipping):比如大于/小于一个固定的阈值,就让梯度等于这个阈值,将梯度限制在一个范围中。(可以缓解梯度爆炸)
- 合理的权重初始和激活函数:本节课讲述重点
- 将乘法变加法:
下面我们重点探讨最后一种方法:合理的权重初始和激活函数
2.2 基本假设:让每层的均值/方差是一个常数
将每层的输出和梯度都看做随机变量
比如第i层有100维,就将输出和梯度分别看成100个随机变量
让它们的均值和方差都保持一致
我们的目标,这样不管神经网络多深,最后一层总与第一层差不多,从而不会梯度爆炸和消失
根据我们的假设,可以列出如下方程式:

2.3 权重初始化
- 在合理值区间里随机初始参数
- 训练开始的时候更容易有数值不稳定
- 远离最优解的地方损失函数表面可能很复杂
- 最优解附近表面会比较平
- 使用N(0, 0.01)分布来初始可能对小网络没问题,但不能保证深度神经网络
2.4 例子:MLP
下面我们以MLP为例,考虑需要什么条件,才能满足2.2节的假设。
2.4.1 模型假设
- 每一层权重中的变量均为独立同分布,并设出均值、方差。
- 每一层输入的变量独立于该层权重变量。同时输入变量之间独立同分布。
- 假设没有激活函数(先简化分析,之后会考虑有激活函数的情况),可以求得该层输出的期望为0。
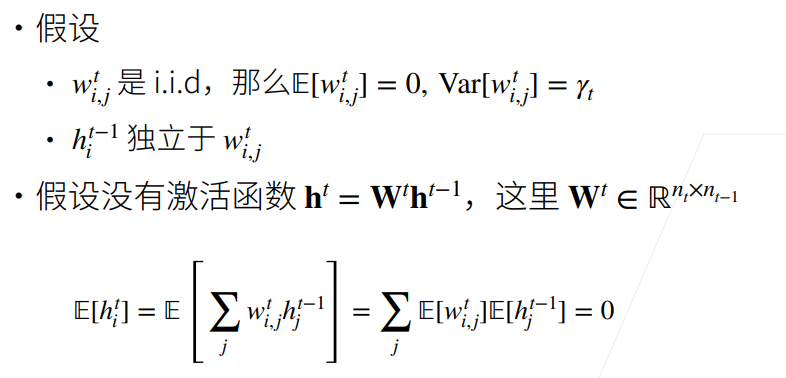
此处用到了一个重要性质:

更多均值、方差运算可以参考期望、方差、协方差及相关系数的基本运算
2.4.2 正向方差
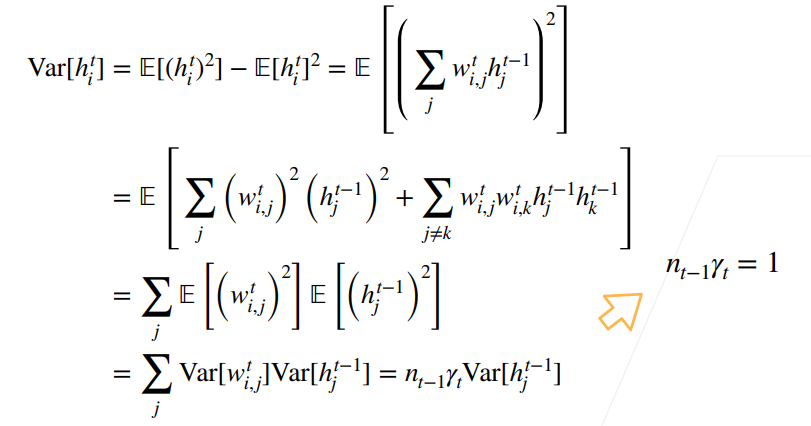
第二行的计算中仍然用到了2.4.1节的期望的重要性质:如果两个变量独立,它们乘积的均值=均值的乘积,再结合w的期望为0(注意w和h独立,w之间独立同分布),即有第二行末项期望为0。
最后一行由于wi,j独立同分布,方差相同,加上做了hj独立同分布的假设,所以可以写成 [t-1层输出维度] x [t层权重方差] x [t-1层输出方差] 的形式
此时,我们回过头来看我们的终极目标2.2节的假设,每层输出期望为0我们已经可以满足(2.4.1节已经推导出),而方差相同这一目标,通过上图的推导,我们发现需要<$n_{t-1}\gamma _{t}=1$。
2.4.3 反向均值和方差

反向的情况和正向的类似,不过此时我们需要满足的式子变为$n_{t}\gamma _{t}=1$。
2.4.4 Xavier初始
上述推导带来的问题:难以同时满足$n_{t-1}\gamma _{t}=1$和$n_{t}\gamma _{t}=1$。(需要每层输出的维度都相同)
采用Xavier折中解决,不能同时满足上面两式,转而满足 [上面两式做加法后除以2] 得到的式子,用两种分布进行初始化(每层方差、均值满足推导式)。

如果能确定每层输入、输出维度大小,则能确定该层权重的方差大小。
- 权重初始化方式:正态分布、均匀分布,均值/方差满足Xavier的假设。
2.4.5 假设线性的激活函数
真实情况下,我们并不会用线性的激活函数(这样相当于没有进行激活),这里为了简化问题,假设激活函数是线性的。
- 正向
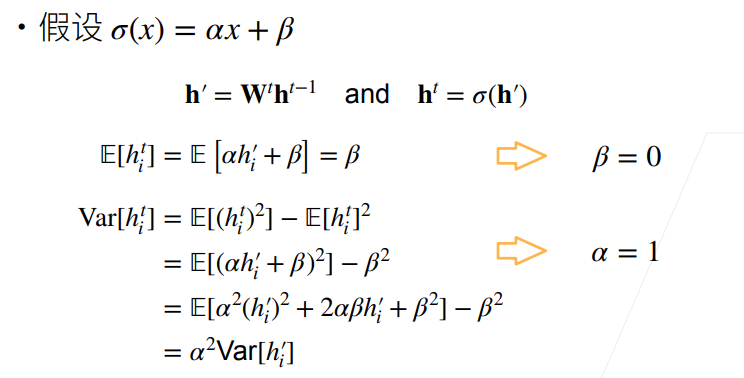
上述推导表明,为了使得前向传播的均值为0,方差固定的话,激活函数必须f(x)=x,这种恒等映射。
- 反向
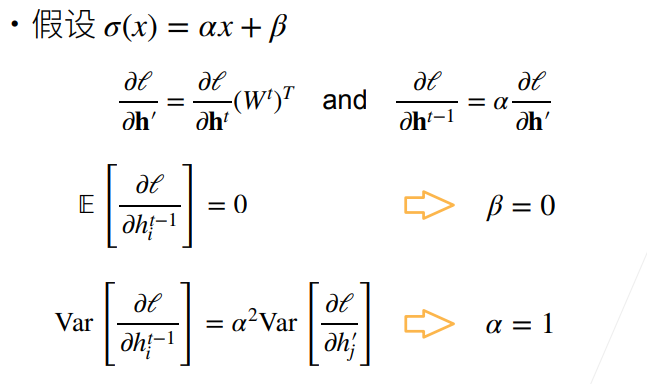
PPT上的推导似乎有点问题(上图中第二行方程),笔者重新进行了下述推导,读者也可自行推导验证:
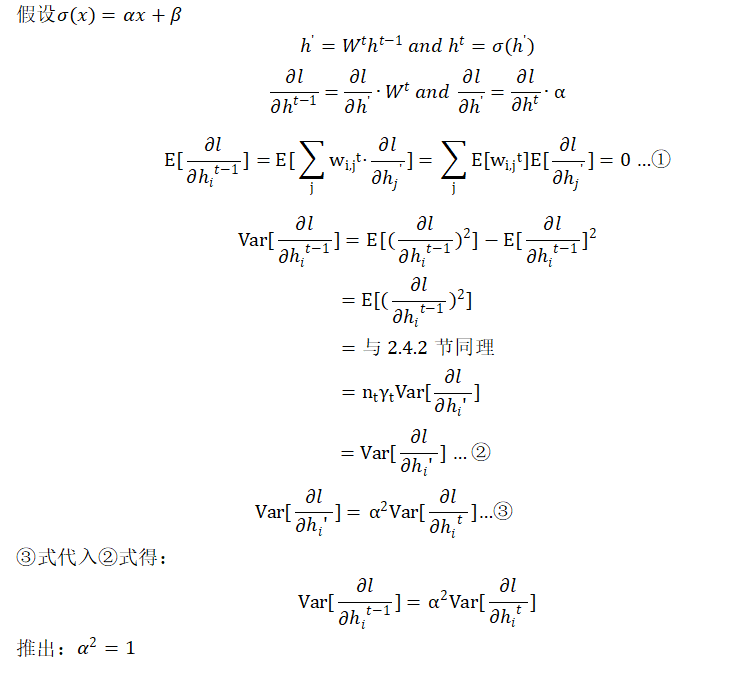
通过正向和反向的推导,我们可以得出的【结论】是:当激活函数为f(x)=x,这种恒等映射更有利于维持神经网络的稳定性。
2.4.6 检查常用激活函数
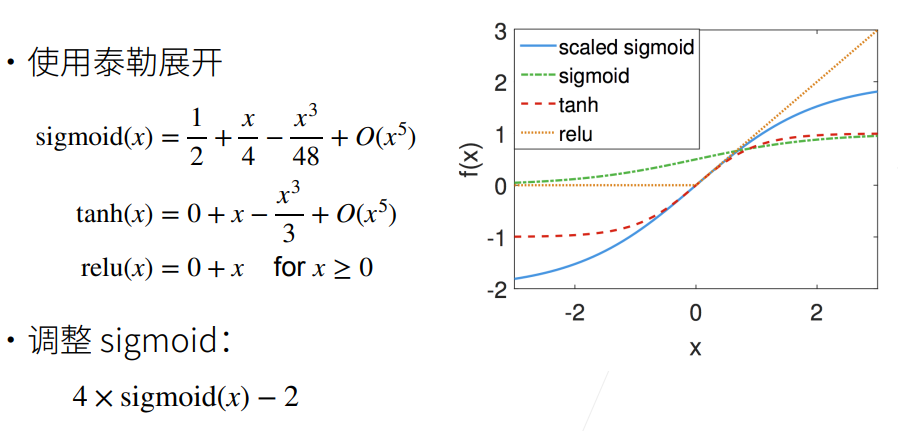
对于常用激活函数:tanh,relu满足在零点附近有f(x)=x,而sigmoid函数在零点附近不满足要求,可以对sigmoid函数进行调整(根据Taylor展开式,调整其过原点)
3. 总结
- 当数值过大或者过小时,会导致数值问题。
常发生在深度模型中,因为其会对n个数累乘。
合理的权重初始值(如Xavier)和激活函数的选取(如relu, tanh, 调整后的sigmoid)可以提升数值稳定性。
4.Q&A
问题:nan, inf是怎么产生的以及怎么解决的?
NaN和Inf怎么产生的:参考出现nan、inf原因
如何解决:参考深度学习中nan和inf的解决以及训练网络loss出现Nan解决办法
问题:训练过程中,如果网络层的输出的中间层特征元素的值突然变成nan了,是发生梯度爆炸了吗?
问题:老师,让每层方差是一个常数的方法,您指的是batch normalization吗?想问一下bn层为什么要有伽马和贝塔?去掉可以吗
让每层方差是一个常数,和batch norm没有太多关系,(本节课介绍的方法是合理地初始化权重和设置激活函数)。batch norm可以让你的输出变成一个均值为0,方差差不多是一个固定值的东西,但它不一定能保证你的梯度。
(此处节选几个重要的Q&A,建议观看完整Q&A,获得更深的理解)