07-链式法则与自动求导

发表于 2024-04-23 更新于 2024-04-24 分类于动手学深度学习阅读次数：

动手学深度学习李沐

更新历史

24.04.24：初稿

系列

动手学深度学习笔记汇总

07-链式法则与自动求导

1. 向量链式法则

1.1 标量链式法则

1.2 拓展到向量
需要注意维数的变化

下图三种情况分别对应：
1. y为标量，x为向量
2. y为标量，x为矩阵
3. y、x为矩阵

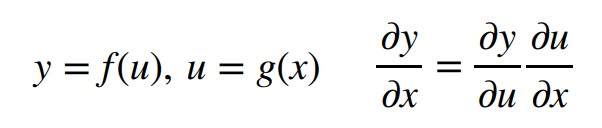
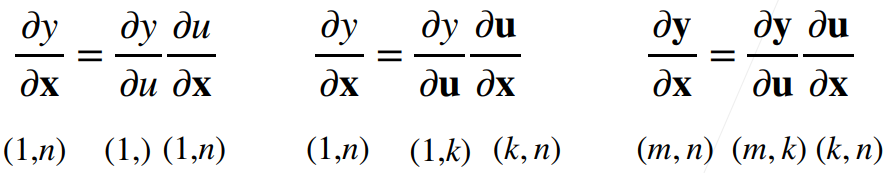
例1（标量对向量求导）

这里应该是用分子布局，所以是X转置

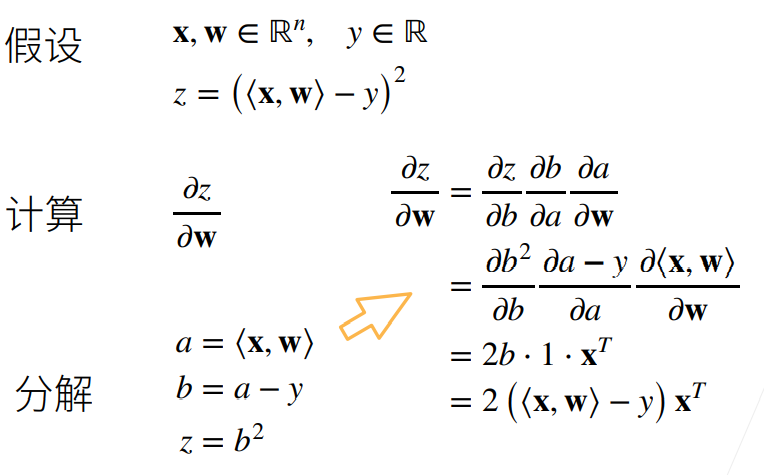
例2（涉及到矩阵的情况）

X是mxn的矩阵,w为n维向量，y为m维向量；
z对Xw-y做L2 norm,为标量；
过程与例一大体一致；

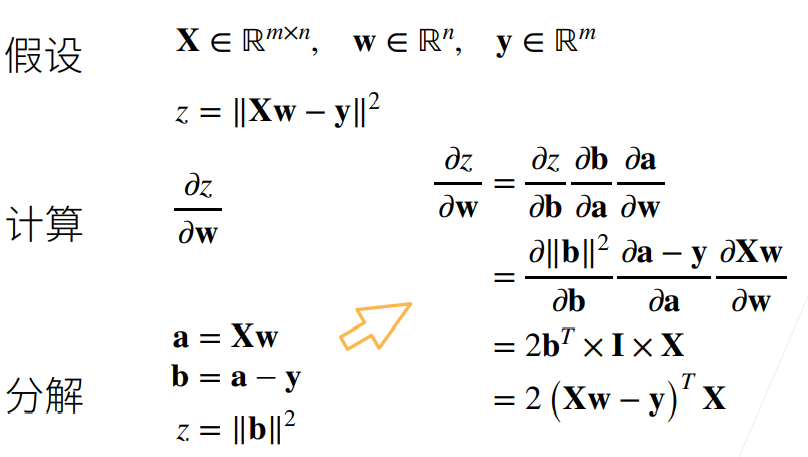
由于在神经网络动辄几百层，手动进行链式求导是很困难的，因此我们需要借助自动求导

2. 自动求导

含义：计算一个函数在指定值上的导数
自动求导有别于
- 符号求导
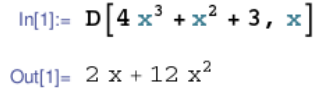
- 数值求导

为了更好地理解自动求导，下面引入计算图的概念

2.1 计算图

将代码分解成操作子
将计算表示成一个无环图

下图自底向上其实就类似于链式求导过程

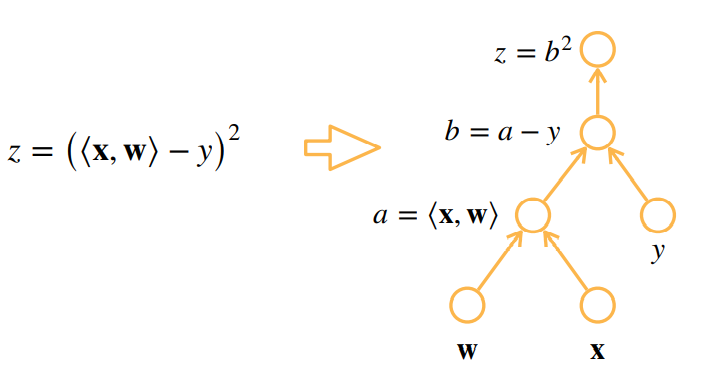
计算图有两种构造方式
计算与上图无关
- 显示构造
  
  可以理解为先定义公式再代值
  
  Tensorflow/Theano/MXNet
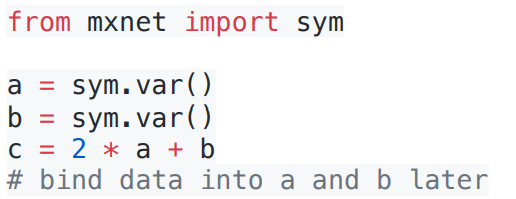
- 隐式构造
  
  系统将所有的计算记录下来
  
  Pytorch/MXNet

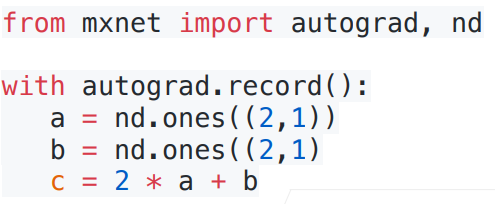
2.2 自动求导的两种模式

正向累积
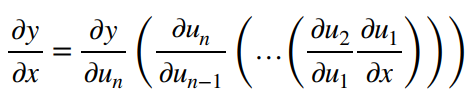
反向累积（反向传递back propagation）

反向累积计算过程

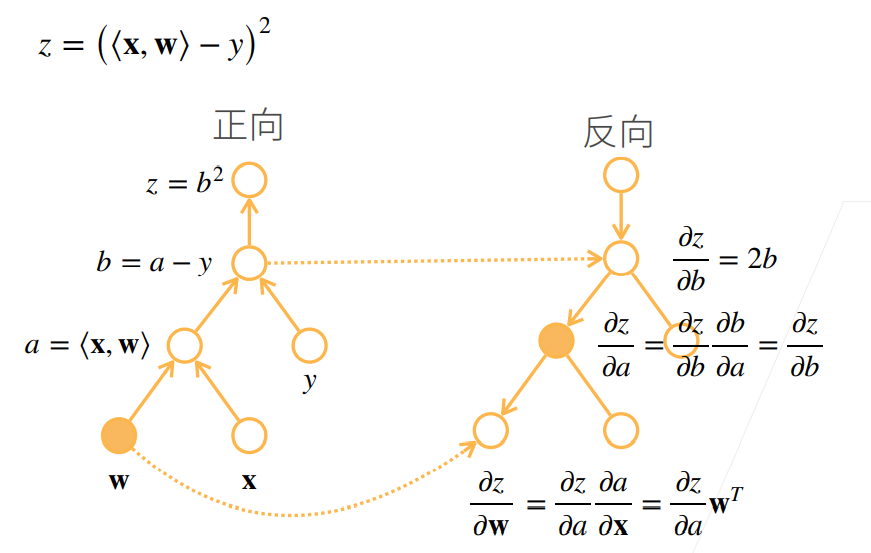
反向累积的正向过程：自底向上，需要存储中间结果

反向累积的反向过程：自顶向下，可以去除不需要的枝（图中的x应为w）

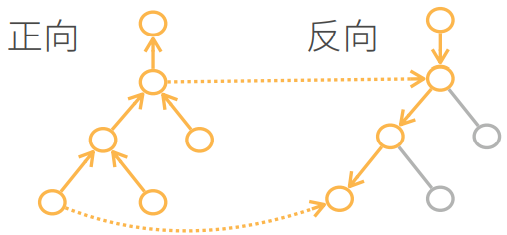
2.3 复杂度比较

反向累积
- 时间复杂度：O(n),n是操作子数
  - 通常正向和反向的代价类似
- 空间复杂度：O(n)
  - 存储正向过程所有的中间结果
正向累积

每次计算一个变量的梯度时都需要将所有节点扫一遍
- 时间复杂度：O(n)
- 空间复杂度：O(1)

3. 代码部分

#对y = x.Tx关于列向量x求导
import torch

x = torch.arange(4.0)
x

tensor([0., 1., 2., 3.])

#存储梯度
x.requires_grad_(True)#等价于x = torch.arange(4.0,requires_grad=True)
x.grad#默认值是None

y = torch.dot(x,x)
y
#PyTorch隐式地构造计算图，grad_fn用于记录梯度计算

tensor(14., grad_fn=<DotBackward0>)

通过调用反向传播函数来自动计算y关于x每个分量的梯度

y.backward()
x.grad

tensor([0., 2., 4., 6.])

x.grad==2*x#验证

tensor([True, True, True, True])

# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()#如果没有这一步结果就会加累上之前的梯度值，变为[1,5,9,13]
y = x.sum()
y.backward()
x.grad

tensor([1., 1., 1., 1.])

x.grad.zero_()
y=x*x#哈达玛积，对应元素相乘

#在深度学习中我们一般不计算微分矩阵
#而是计算批量中每个样本单独计算的偏导数之和

y.sum().backward()#等价于y.backword(torch.ones(len(x)))
x.grad

tensor([0., 2., 4., 6.])

将某些计算移动到记录的计算图之外

# 后可用于用于将神经网络的一些参数固定住
x.grad.zero_()
y = x*x
u = y.detach()#把y当作常数
z = u*x

z.sum().backward()
x.grad == u

tensor([True, True, True, True])

x.grad.zero_()
y.sum().backward()
x.grad == 2*x

tensor([True, True, True, True])

即使构建函数的计算图需要用过Python控制流，仍然可以计算得到的变量的梯度

这也是隐式构造的优势，因为它会存储梯度计算的计算图，再次计算时执行反向过程就可以

def f(a):
    b = a * 2
    while b.norm()<1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(),requires_grad=True)
d = f(a)
d.backward()

a.grad == d / a

4. 自动求导 Q&A

Q1：ppt上隐式构造和显式构造看起来为啥差不多？

显式和隐式的差别其实就是数学上求梯度和python求梯度计算上的差别，不用深究

显式构造就是我们数学上正常求导数的求法，先把所有求导的表达式选出来再代值

Q2:需要正向和反向都算一遍吗？

需要正向先算一遍，自动求导时只进行反向就可以，因为正向的结果已经存储

Q3:为什么PyTorch会默认累积梯度

便于计算大批量；方便进一步设计

Q4:为什么深度学习中一般对标量求导而不是对矩阵或向量求导

loss一般都是标量

Q5:为什么获取.grad前需要backward

相当于告诉程序需要计算梯度，因为计算梯度的代价很大，默认不计算

Q6:pytorch或mxnet框架设计上可以实现矢量的求导吗

可以

5. 练习

1.为什么计算二阶导数比一阶导数的开销要更大？

二阶导数是在一阶导数的基础上进行的，开销自然更大

2.在运行反向传播函数之后，立即再次运行它，看看会发生什么。

“RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.”

说明不能连续两次运行,pytorch使用的是动态计算图,反向传播函数运行一次后计算图就被释放了

只需要在函数接口将参数retain_graph设为True即可

In [51]:

def f(a):
    b = a * 2
    while b.norm()<1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c
a.grad.zero_()
a = torch.randn(size=(),requires_grad=True)#size=0表示a是标量
d = f(a)
#d.backward(retain_graph=True)
#a.grad
d.backward()
a.grad

Out[51]:

tensor(4096.)

3.在控制流的例子中，我们计算d关于a的导数，如果我们将变量a更改为随机向量或矩阵，会发生什么？此时，计算结果f(a)不再是标量。结果会发生什么？我们如何分析这个结果？

backward函数的机制本身不允许张量对张量求导，如果输入是向量或矩阵，需要将其在各个分量上求和，变为标量；所以还需要传入一个与输入同型的张量

In [53]:

def f(a):
    b = a * 2
    while b.norm()<1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c
a.grad.zero_()
a = torch.randn(10,requires_grad=True)
d = f(a)
#d.backward(retain_graph=True)
#a.grad
#d.backward()#RuntimeError: grad can be implicitly created only for scalar outputs
d.sum().backward()#需要加上.sum()否则会报错 
a.grad

Out[53]:

tensor([51200., 51200., 51200., 51200., 51200., 51200., 51200., 51200., 51200.,
        51200.])

4.重新设计一个求控制流梯度的例子。运行并分析结果。

In [56]:

def h(x):
    y = x * x
    while y.norm() < 2500:
        y = y * 2
    if y.sum() < 0:
        c = 100*y
    else:
        c = y
    return c
x.grad.zero_()
x = torch.randn(size=(),requires_grad=True)
y = h(x)
y.backward()
x.grad

Out[56]:

tensor(-3311.5398)

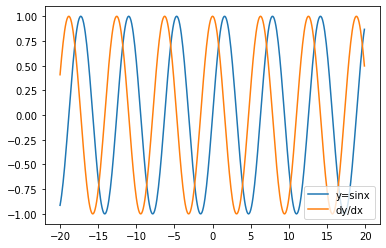
5.使f(x)=sin(x)，绘制f(x)和df(x)/dx的图像，其中后者不使用f’(x)=\cos(x)。

In [66]:

import matplotlib.pyplot as plt
x = torch.arange(-20,20,0.1,requires_grad=True,dtype=torch.float32)
y = torch.sin(x)
y.sum().backward()
plt.plot(x.detach(),y.detach(),label='y=sinx')
plt.plot(x.detach(),x.grad,label='dy/dx')
plt.legend(loc='lower right')

Out[66]:

<matplotlib.legend.Legend at 0x1d627d00280>

系列

07-链式法则与自动求导

1. 向量链式法则

1.1 标量链式法则

1.2 拓展到向量

例1（标量对向量求导）

例2（涉及到矩阵的情况）

2. 自动求导

2.1 计算图

2.2 自动求导的两种模式

2.3 复杂度比较

3. 代码部分

4. 自动求导 Q&A

5. 练习