机器学习笔记二 多变量线性回归
更新历史
- 24.04.21:初稿
系列
4 多变量线性回归(Linear Regression with Multiple Variables)
4.1 多特征(Multiple Features)
不同维度的多个特征。
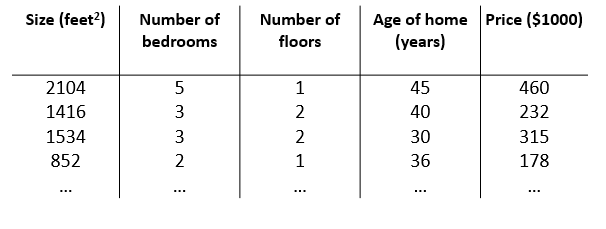
这里由于特征不再只有一个,引入一些新的记号
$n$: 特征的总数
${x}^{\left( i \right)}$: 代表样本矩阵中第 $i$ 行,也就是第 $i$ 个训练实例。
${x}_{j}^{\left( i \right)}$: 代表样本矩阵中第 $i$ 行的第 $j$ 列,也就是第 $i$ 个训练实例的第 $j$ 个特征。
参照上图,则有 ${x}^{(2)}\text{=}\begin{bmatrix} 1416\\\ 3\\\ 2\\\ 40 \end{bmatrix}, {x}^{(2)}_{1} = 1416$
全部写成一维向量
多变量假设函数 $h$ 表示为:$h_{\theta}\left( x \right)={\theta_{0} }+{\theta_{1} }{x_{1} }+{\theta_{2} }{x_{2} }+…+{\theta_{n} }{x_{n} }$
对于 $\theta_0$,和单特征中一样,我们将其看作基础数值。
$$
h_\theta\left(x\right)=\begin{bmatrix}\theta_0\; \theta_1\; … \;\theta_n \end{bmatrix}\begin{bmatrix}x_0 \newline x_1 \newline \vdots \newline x_n\end{bmatrix}= \theta^T x
$$
$\theta^T$: $\theta$ 矩阵的转置
$x$: 某个样本的特征向量,$n+1$ 维特征量向量
$x_0$: 为了计算方便我们会假设 $x_0^{(i)} = 1$
4.2 多变量梯度下降(Gradient Descent for Multiple Variables)
多变量代价函数类似于单变量代价函数,
即 $J\left( {\theta_{0} },{\theta_{1} }…{\theta_{n} } \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{ { {\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2} } }$ ,其中 $h_\theta\left(x\right)= \theta^T x$。
前文提到梯度下降对于最小化代价函数的通用性,则多变量梯度下降公式即
\begin{split}
& \text{Repeat until convergence:} \; \lbrace \\
&{ {\theta }_{j} }:={ {\theta }_{j} }-\alpha \frac{\partial }{\partial { {\theta }_{j} } }J\left( {\theta_{0} },{\theta_{1} }…{\theta_{n} } \right) \\
\rbrace
\end{split}
解出偏导得:
\begin{split}
& \text{repeat until convergence:} \; \lbrace \\
& \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; & \text{for j := 0,1…n}\\
\rbrace
\end{split}
可展开为:
\begin{split}
& \text{repeat until convergence:} \; \lbrace \\
& \theta_0 := \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_0^{(i)}\\
& \theta_1 := \theta_1 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_1^{(i)} \\
& \theta_2 := \theta_2 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_2^{(i)} \\
& \vdots \\
& \theta_n := \theta_n - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_n^{(i)} &\\
\rbrace
\end{split}
当然,同单变量梯度下降一样,计算时需要同时更新所有参数。
$h_\theta\left(x\right)= \theta^T x$,则得到同时更新参数的向量化(Vectorization)实现:
$$
\theta = \theta - \alpha \frac{1}{m}(X^T(X\theta-y))
$$
向量化推导过程:
\begin{split}
&X = \begin{bmatrix}{ {x}^{(0)} } ^ T \newline { {x}^{(1)} } ^ T \newline \vdots \newline { {x}^{(m)} } ^ T\ \end{bmatrix}
&X^T = \begin{bmatrix}{x}^{(0)}\; {x}^{(1)}\; … \;{x}^{(m)} \end{bmatrix}
\\
&X\theta - y = \begin{bmatrix}{ {x}^{(0)} } ^ T \theta - y\newline { {x}^{(1)} } ^ T \theta -y \newline \vdots \newline { {x}^{(m)} } ^ T\theta -y\ \end{bmatrix} \\
&h_\theta\left(x\right)= X\theta
\end{split}
$X$: 是一个秩为1的矩阵? 一次更新一个相同的特征向量??
$X$: 训练集数据,$m\times(n+1)$ 维矩阵(包含基本特征 $x_0=1$)
4.3 梯度下降实践1-特征值缩放(Gradient Descent in Practice I - Feature Scaling)
在应用梯度下降算法实践时,由于各特征值的范围不一,可能会影响代价函数收敛速度。
房屋面积大小和房间数量这两个特征。
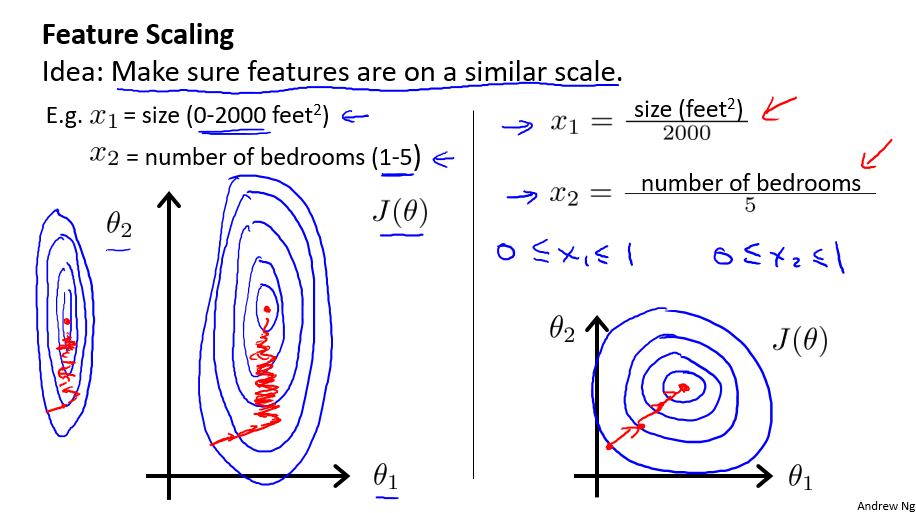
为了优化梯度下降的收敛速度,采用特征缩放的技巧,使各特征值的范围尽量一致。
除了以上图人工选择并除以一个参数的方式,均值归一化(Mean normalization方法更为便捷,可采用它来对所有特征值统一缩放:
$x_i:=\frac{x_i-average(x)}{maximum(x)-minimum(x)}$, 使得 $x_i \in (-1,1)$
对于特征的范围,并不一定需要使得 $-1 \leqslant x \leqslant 1$,类似于 $1\leqslant x \leqslant 3$ 等也是可取的,而诸如 $-100 \leqslant x \leqslant 100 $,$-0.00001 \leqslant x \leqslant 0.00001$,就显得过大/过小了。
另外注意,一旦采用特征缩放,我们就需对所有的输入采用特征缩放,包括训练集、测试集、预测输入等。
4.4 梯度下降实践2-学习速率(Gradient Descent in Practice II - Learning Rate)
通常,有两种方法来确定函数是否收敛
- 多次迭代收敛法
- 无法确定需要多少次迭代
- 较易绘制关于迭代次数的图像
- 根据图像易预测所需的迭代次数
- 自动化测试收敛法(比较阈值)
- 不易选取阈值
- 代价函数近乎直线时无法确定收敛情况
对于梯度下降,一般采用多次迭代收敛法来得出最小化代价函数的参数值,自动化测试收敛法(如设定 $J\left(\theta\right) < {10}^{-3}$ 时判定收敛)则几乎不会被使用。
我们可以通过绘制代价函数关于迭代次数的图像,可视化梯度下降的执行过程,借助直观的图形来发现代价函数趋向于多少时能趋于收敛,依据图像变化情况,确定诸如学习速率的取值,迭代次数的大小等问题。
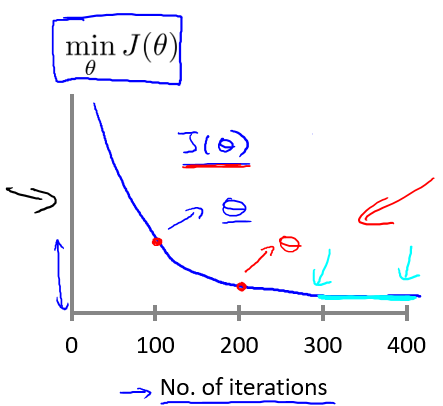
对于学习速率 $\alpha$,一般上图展现的为适中情况,下图中,左图可能表明 $\alpha$ 过大,代价函数无法收敛,右图可能表明 $\alpha$ 过小,代价函数收敛的太慢。当然,$\alpha$ 足够小时,代价函数在每轮迭代后一定会减少。
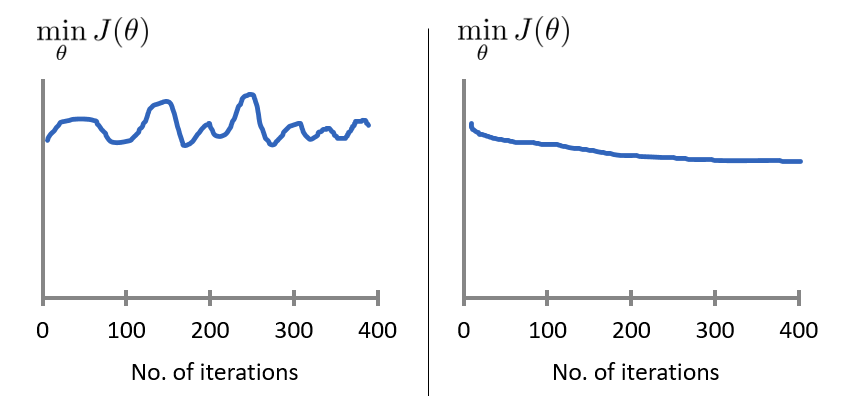
通过不断改变 $\alpha$ 值,绘制并观察图像,并以此来确定合适的学习速率。 尝试时可取 $\alpha$ 如 $\dots\;0,001,\;0.003,\;0.01,\;0.03,\;0.1,\;\dots$
4.5 特征和多项式回归(Features and Polynomial Regression)
在特征选取时,我们也可以自己归纳总结,定义一个新的特征,用来取代或拆分旧的一个或多个特征。比如,对于房屋面积特征来说,我们可以将其拆分为长度和宽度两个特征,反之,我们也可以合并长度和宽度这两个特征为面积这一个特征。
线性回归只能以直线来对数据进行拟合,有时候需要使用曲线来对数据进行拟合,即多项式回归(Polynomial Regression)。
比如一个二次方模型:$h_{\theta}\left( x \right)={\theta_{0} }+{\theta_{1} }{x_{1} }+{\theta_{2} }{x_{2}^2}$
或者三次方模型:$h_{\theta}\left( x \right)={\theta_{0} }+{\theta_{1} }{x_{1} }+{\theta_{2} }{x_{2}^2}+{\theta_{3} }{x_{3}^3}$
或者平方根模型: $h_{\theta}\left( x \right)={\theta_{0} }+{\theta_{1} }{x_{1} }+{\theta_{2} }{x_{2}^2}+{\theta_{3} }{\sqrt{x_3} }$
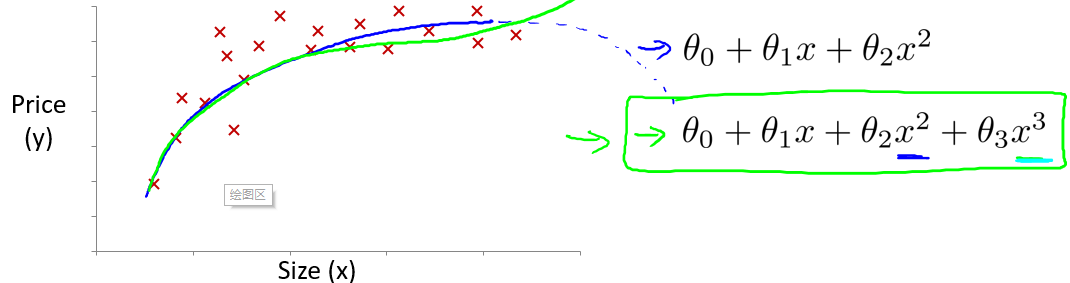
在使用多项式回归时,要记住非常有必要进行特征缩放,比如 $x_1$ 的范围为 1-1000,那么 $x_1^2$ 的范围则为 1- 1000000,不使用特征缩放的话,范围不一致,也更易影响效率。
多特征下的特征值缩放按照$x$还是$x^3$ ?
4.6 正规方程(Normal Equation)
对于一些线性回归问题来说,正规方程法给出了一个更好的解决问题的方式。
正规方程法,即令 $\frac{\partial}{\partial{\theta_{j} } }J\left( {\theta_{j} } \right)=0$ ,通过解析函数的方式直接计算得出参数向量的值 $\theta ={ {\left( {X^T}X \right)}^{-1} }{X^{T} }y$ ,Octave/Matlab 代码: theta = inv(X'*X)*X'*y。
${X}^{-1}$: 矩阵 $X$ 的逆,在 Octave 中,
inv函数用于计算矩阵的逆,类似的还有pinv函数。
X': 在 Octave 中表示矩阵 X 的转置,即 $X^T$
下表列出了正规方程法与梯度下降算法的对比
| 条件 | 梯度下降 | 正规方程 |
|---|---|---|
| 是否需要选取 $\alpha$ | 需要 | 不需要 |
| 是否需要迭代运算 | 需要 | 不需要 |
| 特征量大时 | 适用,$O\left(kn^2\right)$ | 不适用,$(X^TX)^{-1}$ 复杂度 $O\left( { {n}^{3} } \right)$ |
| 适用范围 | 各类模型 | 只适用线性模型,且矩阵需可逆 |
- 一般来说,当 $n$ 超过 10000 时,对于正规方程而言,特征量较大。
- 梯度下降算法的普适性好,而对于特定的线性回归模型,正规方程是很好的替代品。
正规方程法的推导过程:(同4.2)
\begin{split}
J\left( \theta \right)& =\frac{1}{2m}\sum\limits_{i=1}^{m}{ { {\left( {h_{\theta} }\left( {x^{(i)} } \right)-{y^{(i)} } \right)}^{2} } }\\
& =\frac{1}{2m}||X\theta-y||^2 \\
& =\frac{1}{2m}(X\theta-y)^T(X\theta-y) \hspace{15cm}
\end{split}
展开上式可得
$
(X\theta-y)^T = \theta^T X^T - y^T
$
$J(\theta )= \frac{1}{2m}\left( { {\theta }^{T} }{ {X}^{T} }X\theta -{ {\theta}^{T} }{ {X}^{T} }y-{ {y}^{T} }X\theta + { {y}^{T} }y \right)$
注意到 ${ {\theta}^{T} }{ {X}^{T} }y$ 与 ${ {y}^{T} }X\theta$ 都为标量,实际上是等价的,则:
$J(\theta) = \frac{1}{2m}[{\theta }^{T}X^TX\theta-2\theta^TX^Ty+y^Ty]$
接下来对$J(\theta )$ 求偏导,根据矩阵的求导法则:
$\frac{d X^TAX}{d X}=2AX$
$\frac{d X^T}{d X}={E}$
$\frac{d AB}{d B}={A^T}$
所以有:
$\frac{\partial J\left( \theta \right)}{\partial \theta }=\frac{1}{2m}\left(2{ {X}^{T} }X\theta -2{ {X}^{T} }y \right)={ {X}^{T} }X\theta -{ {X}^{T} }y$
令$\frac{\partial J\left( \theta \right)}{\partial \theta }=0$, 则有
$$
\theta ={ {\left( {X^{T} }X \right)}^{-1} }{X^{T} }y
$$
求最小值, 极值一定是最小值, 具有实际意义
4.7 不可逆性正规方程(Normal Equation Noninvertibility)
(本部分内容为选讲)
正规方程无法应用于不可逆的矩阵,发生这种问题的概率很小,通常由于
特征之间线性相关
比如同时包含英寸的尺寸和米为单位的尺寸两个特征,它们是线性相关的
即 ${x_{1} }={x_{2} }*{ {\left( 3.28 \right)}^{2} }$。
特征数量大于训练集的数量 $\left(m \leqslant n \right)$。
如果发现 $X^TX$ 的结果不可逆,可尝试:
- 减少多余/重复特征
- 增加训练集数量
- 使用正规化(后文)
对于这类不可逆的矩阵,我们称之为奇异矩阵或退化矩阵。
这种情况下,如果还想使用正规方程法,在Octave中,可以选用 pinv 函数,pinv 区别于 inv,pinv 函数被称为伪逆函数,在矩阵不可逆的时候,使用这个函数仍可正确地计算出 $\theta$ 的值。