机器学习笔记一 单变量线性回归
更新历史
- 24.04.18:初稿
系列
1 引言(Introduction)
1.1 Welcome
随着互联网数据不断累积,硬件不断升级迭代,在这个信息爆炸的时代,机器学习已被应用在各行各业中,可谓无处不在。
1.2 什么是机器学习(What is Machine Learning)
机器学习定义
这里主要有两种定义:Arthur Samuel (1959). Machine Learning:
Field of study that gives computers the ability to learn without being explicitly programmed.
这个定义有点不正式但提出的时间最早,来自于一个懂得计算机编程的下棋菜鸟。他编写了一个程序,但没有显式地编程每一步该怎么走,而是让计算机自己和自己对弈,并不断地计算布局的好坏,来判断什么情况下获胜的概率高,从而积累经验,好似学习,最后,这个计算机程序成为了一个比他自己还厉害的棋手。Tom Mitchell (1998) Well-posed Learning Problem:
A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
Tom Mitchell 的定义更为现代和正式。在过滤垃圾邮件这个例子中,电子邮件系统会根据用户对电子邮件的标记(是/不是垃圾邮件)不断学习,从而提升过滤垃圾邮件的准确率,定义中的三个字母分别代表:- T(Task): 过滤垃圾邮件任务。
- P(Performance): 电子邮件系统过滤垃圾邮件的准确率。
- E(Experience): 用户对电子邮件的标记。
类似监督学习
- 机器学习算法
主要有两种机器学习的算法分类- 监督学习
- 无监督学习
还有一些算法也属于机器学习领域,诸如:
- 半监督学习: 介于监督学习于无监督学习之间
- 推荐算法:
- 强化学习: 通过观察来学习如何做出动作,每个动作都会对环境有所影响,而环境的反馈又可以引导该学习算法。
- 迁移学习: 某个领域应用到另个领域
1.3 监督学习(Supervised Learning)
监督学习,即为教计算机如何去完成预测任务(有反馈),预先给一定数据量的输入和对应的结果即训练集,建模拟合,最后让计算机预测未知数据的结果。
监督学习一般有两种:
回归问题(Regression)
回归问题即为预测一系列的连续值。
在房屋价格预测的例子中,给出了一系列的房屋面积数据,根据这些数据来预测任意面积的房屋价格。给出照片-年龄数据集,预测给定照片的年龄。分类问题(Classification)
分类问题即为预测一系列的离散值。
即根据数据预测被预测对象属于哪个分类。
视频中举了癌症肿瘤这个例子,针对诊断结果,分别分类为良性或恶性。还例如垃圾邮件分类问题,也同样属于监督学习中的分类问题。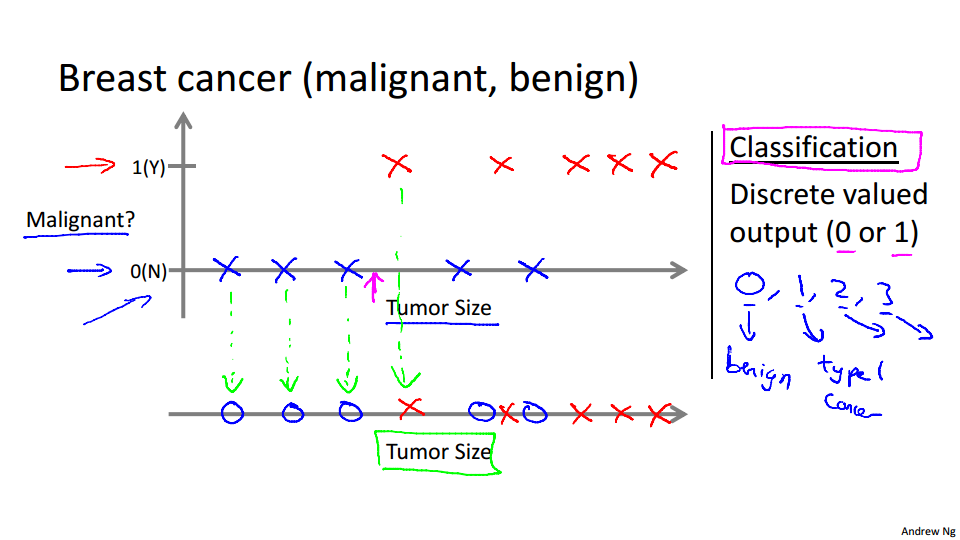
视频中提到支持向量机这个算法,旨在解决当特征量很大的时候(特征即如癌症例子中的肿块大小,颜色,气味等各种特征),计算机内存一定会不够用的情况。支持向量机能让计算机处理无限多个特征。
1.4 无监督学习(Unsupervised Learning)
相对于监督学习,训练集不会有人为标注的结果(无反馈),我们不会给出结果或无法得知训练集的结果是什么样,而是单纯由计算机通过无监督学习算法自行分析,从而“得出结果”。计算机可能会把特定的数据集归为几个不同的簇,故叫做聚类算法。
无监督学习一般分为两种:
- 聚类(Clustering)
- 新闻聚合
- DNA 个体聚类
- 天文数据分析
- 市场细分
- 社交网络分析
- 非聚类(Non-clustering)
- 鸡尾酒问题
新闻聚合
在例如谷歌新闻这样的网站中,每天后台都会收集成千上万的新闻,然后将这些新闻分组成一个个的新闻专题,这样一个又一个聚类,就是应用了无监督学习的结果。
鸡尾酒问题
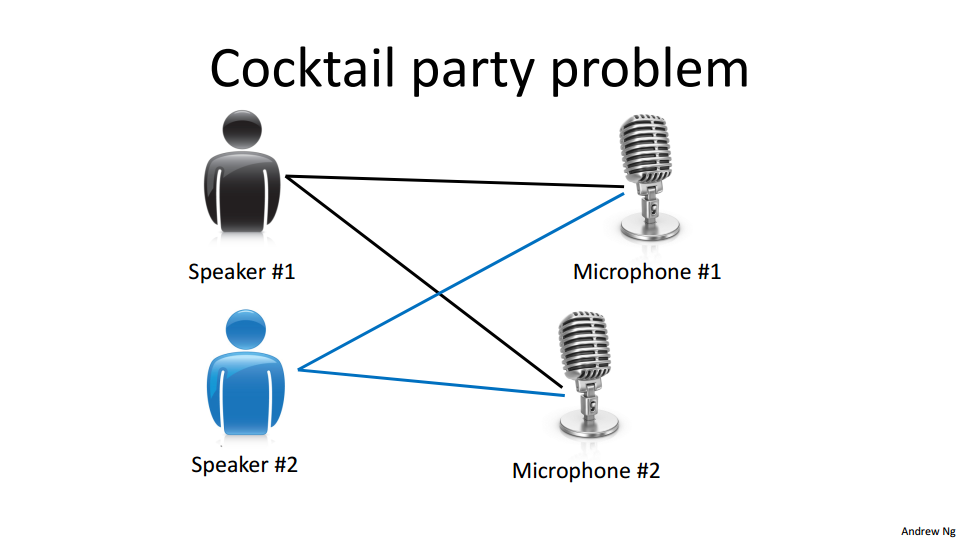
在鸡尾酒会上,大家说话声音彼此重叠,几乎很难分辨出面前的人说了什么。我们很难对于这个问题进行数据标注,而这里的通过机器学习的无监督学习算法,就可以将说话者的声音同背景音乐分离出来。
2 单变量线性回归(Linear Regression with One Variable)
2.1 模型表示(Model Representation)
- 房价预测训练集
| Size in $feet^2$ ($x$) | Price ($) in 1000’s($y$) |
|---|---|
| 2104 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
| … | … |
房价预测训练集中,同时给出了输入 $x$ 和输出结果 $y$,即给出了人为标注的“正确结果”,且预测的量是连续的,属于监督学习中的回归问题。
问题解决模型
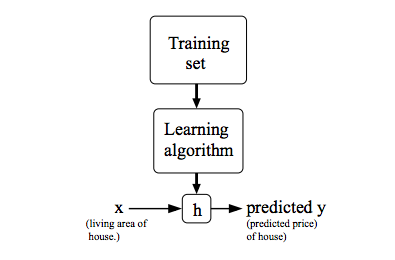
其中 $h$ 代表结果函数,也称为假设(hypothesis) 。假设函数根据输入(房屋的面积),给出预测结果输出(房屋的价格),即是一个 $X\to Y$ 的映射。
$h_\theta(x)=\theta_0+\theta_1x$,为解决房价问题的一种可行表达式。
$x$: 特征/输入变量。
上式中,$\theta$ 为参数,$\theta$ 的变化才决定了输出结果,不同以往,这里的 $x$ 被我们视作已知(不论是数据集还是预测时的输入),所以怎样解得 $\theta$ 以更好地拟合数据,成了求解该问题的最终问题。
单变量,即只有一个特征(如例子中房屋的面积这个特征)。
2.2 代价函数(Cost Function)
李航《统计学习方法》一书中,损失函数与代价函数两者为同一概念,未作细分区别,全书没有和《深度学习》一书一样混用,而是统一使用损失函数来指代这类类似概念。
吴恩达(Andrew Ng)老师在其公开课中对两者做了细分。
损失函数(Loss/Error Function): 计算单个样本的误差。
代价函数(Cost Function): 计算整个训练集所有损失函数之和的平均值
我们的目的在于求解预测结果 $h$ 最接近于实际结果 $y$ 时 $\theta$ 的取值,则问题可表达为求解 $\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})$ 的最小值。
$m$: 训练集中的样本总数
$y$: 目标变量/输出变量
$\left(x, y\right)$: 训练集中的实例
$\left(x^{\left(i\right)},y^{\left(i\right)}\right)$: 训练集中的第 $i$ 个样本实例
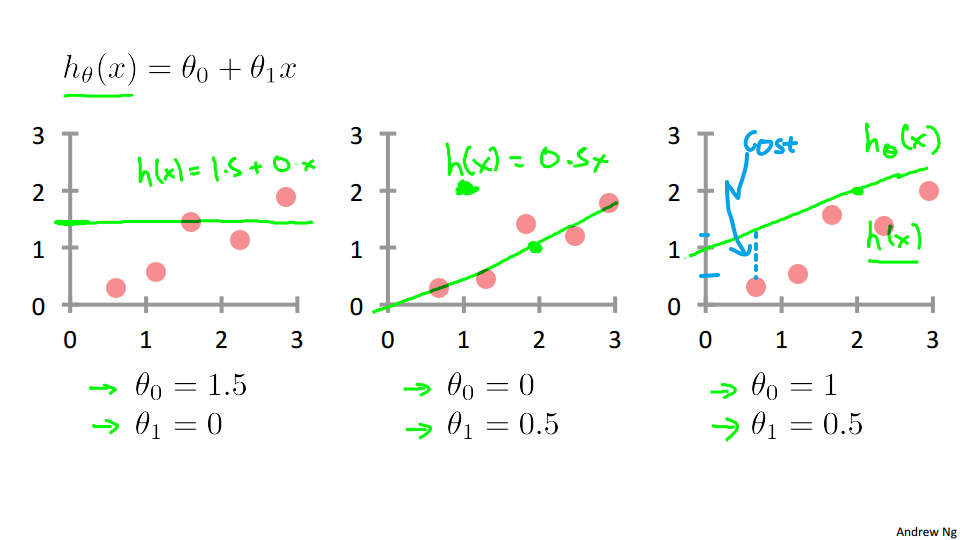
上图展示了当 $\theta$ 取不同值时,$h_\theta\left(x\right)$ 对数据集的拟合情况,蓝色虚线部分代表建模误差。
为了求解最小值,引入代价函数(Cost Function)概念,用于度量建模误差。考虑到要计算最小值,应用二次函数对求和式建模,即应用统计学中的平方损失函数(最小二乘法):
$$
J(\theta_0, \theta_1)= \dfrac{ 1 }{ 2m } \displaystyle \sum_ {i=1}^m\left(\hat{y}_{i}-y_{i} \right)^2=\dfrac{1}{2m}\displaystyle\sum_{i=1}^m\left(h_\theta(x_{i})-y_{i}\right)^2
$$
$\hat{y}$: $y$ 的预测值
系数 $\frac{1}{2}$ 存在与否都不会影响结果,这里是为了在应用梯度下降时便于求解,平方的导数会抵消掉 $\frac{1}{2}$ 。
讨论到这里,我们的问题就转化成了求解 $J\left( \theta_0, \theta_1 \right)$ 的最小值。
2.3 代价函数 - 直观理解1(Cost Function - Intuition I)
根据上节视频,列出如下定义:
- 假设函数(Hypothesis): $h_\theta(x)=\theta_0+\theta_1x$
- 参数(Parameters): $\theta_0, \theta_1$
- 代价函数(Cost Function): $J\left( \theta_0, \theta_1 \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{ { {\left( { {h}_{\theta } }\left( { {x}^{(i)} } \right)-{ {y}^{(i)} } \right)}^{2} } }$
- 目标(Goal): $\underset{\theta_0, \theta_1}{\text{minimize} } J \left(\theta_0, \theta_1 \right)$
为了直观理解代价函数到底是在做什么,先假设 $\theta_0 = 0$,并假设训练集有三个数据,分别为$\left(1, 1\right), \left(2, 2\right), \left(3, 3\right)$,这样在平面坐标系中绘制出 $h_\theta\left(x\right)$ ,并分析 $J\left(\theta_0, \theta_1\right)$ 的变化。
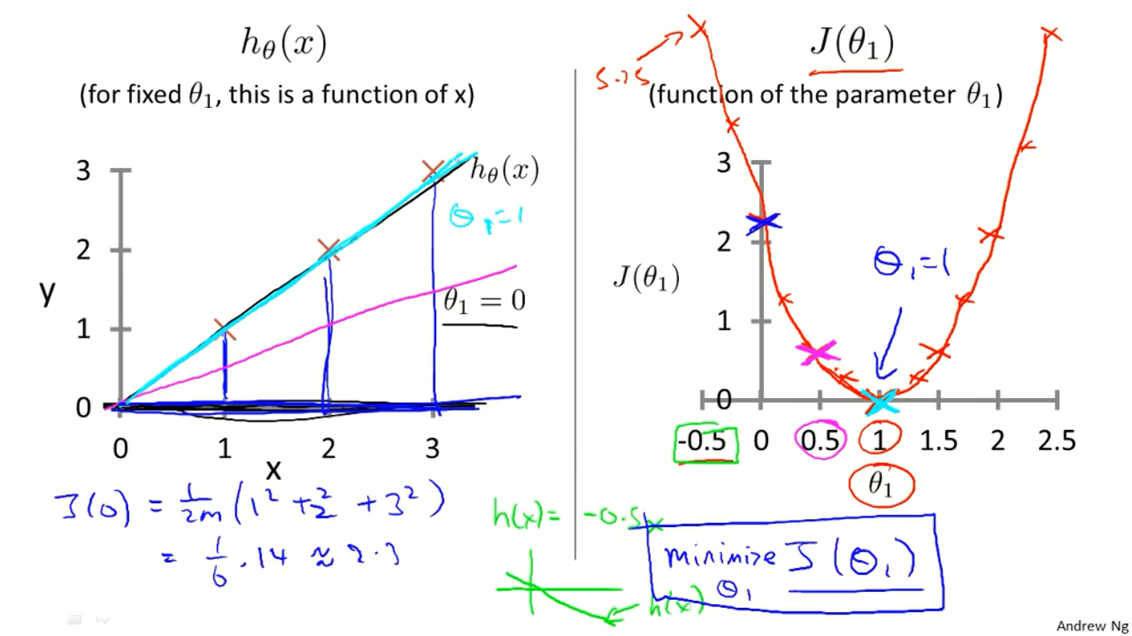
右图 $J\left(\theta_0, \theta_1\right)$ 随着 $\theta_1$ 的变化而变化,可见当 $\theta_1 = 1$ 时,$J\left(\theta_0, \theta_1 \right) = 0$,取得最小值,对应于左图青色直线,即函数 $h$ 拟合程度最好的情况。
2.4 代价函数 - 直观理解2(Cost Function - Intuition II)
给定数据集: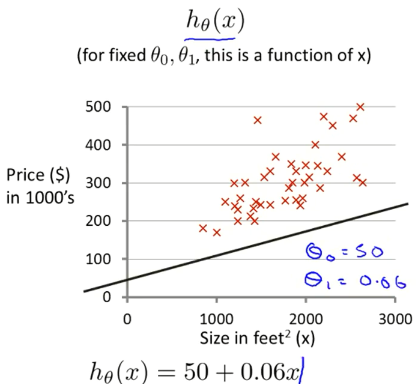
参数在 $\theta_0$ 不恒为 $0$ 时代价函数 $J\left(\theta\right)$ 关于 $\theta_0, \theta_1$ 的3-D图像,图像中的高度为代价函数的值。
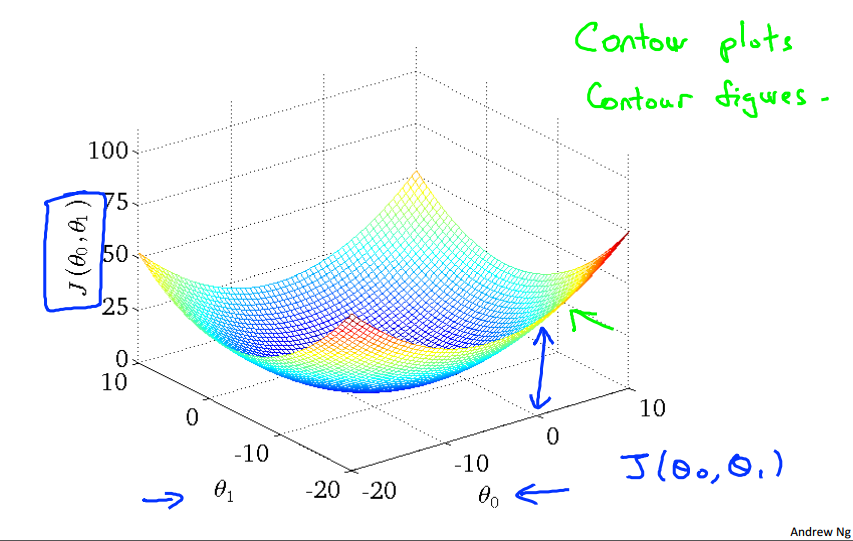
由于3-D图形不便于标注,所以将3-D图形转换为轮廓图(contour plot),下面用轮廓图(下图中的右图)来作直观理解,其中相同颜色的一个圈代表着同一高度(同一 $J\left(\theta\right)$ 值)。
$\theta_0 = 360, \theta_1 =0$ 时:
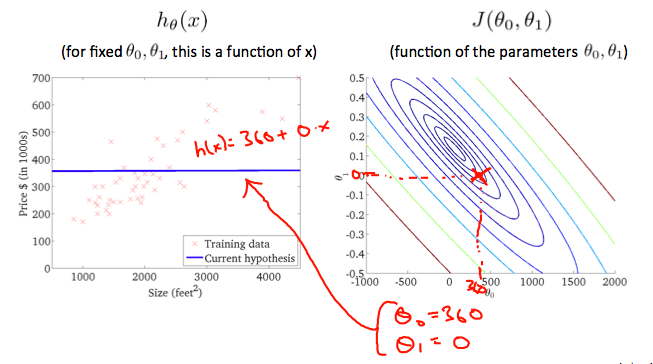
大概在 $\theta_0 = 0.12, \theta_1 =250$ 时:
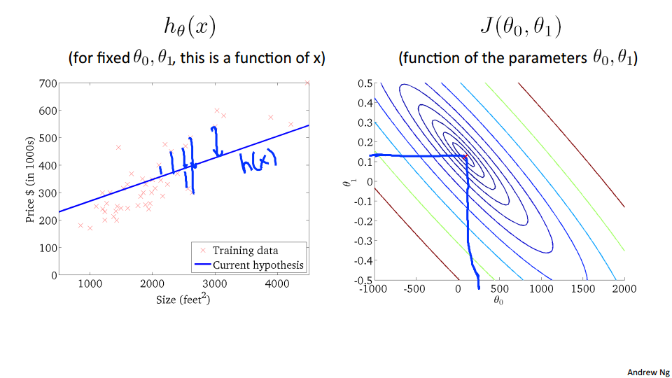
上图中最中心的点(红点),近乎为图像中的最低点,也即代价函数的最小值,此时对应 $h_\theta\left(x\right)$ 对数据的拟合情况如左图所示。
2.5 梯度下降(Gradient Descent)
在特征量很大的情况下,即便是借用计算机来生成图像,人工的方法也很难读出 $J\left(\theta\right)$ 的最小值,并且大多数情况无法进行可视化,故引入梯度下降(Gradient Descent)方法,让计算机自动找出最小化代价函数时对应的 $\theta$ 值。
梯度下降背后的思想是:开始时,我们随机选择一个参数组合$\left( {\theta_{0} },{\theta_{1} },……,{\theta_{n} } \right)$即起始点,计算代价函数,然后寻找下一个能使得代价函数下降最多的参数组合。不断迭代,直到找到一个局部最小值(local minimum),由于下降的情况只考虑当前参数组合周围的情况,所以无法确定当前的局部最小值是否就是全局最小值(global minimum),不同的初始参数组合,可能会产生不同的局部最小值。
下图根据不同的起始点,产生了两个不同的局部最小值。
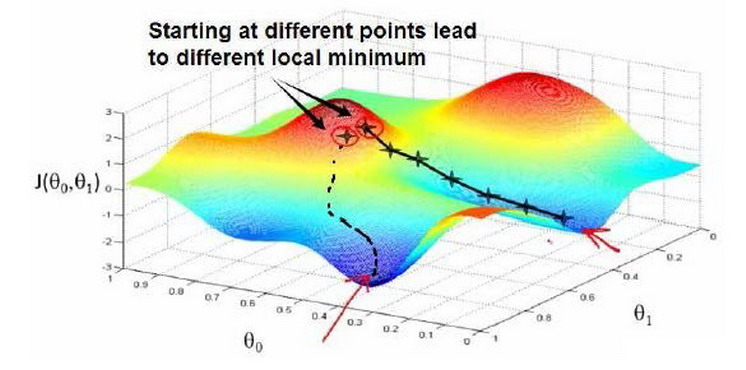
视频中举了下山的例子,即我们在山顶上的某个位置,为了下山,就不断地看一下周围下一步往哪走下山比较快,然后就迈出那一步,一直重复,直到我们到达山下的某一处陆地。
梯度下降公式:
$$
\begin{split}
& \text{Repeat until convergence:} \; \lbrace \\
&{ {\theta }_{j} }:={ {\theta }_{j} }-\alpha \frac{\partial }{\partial { {\theta }_{j} } }J\left( {\theta_{0} },{\theta_{1} } \right) \\
\rbrace
\end{split}
$$
“-”来源于:正值向左移动减少,负值向右移动增加
${\theta }_{j}$: 第 $j$ 个特征参数”:=“: 赋值操作符
$\alpha$: 学习速率(learning rate), $\alpha > 0$
$\frac{\partial }{\partial { {\theta }_{j} } }J\left( \theta_0, \theta_j \right)$: $J\left( \theta_0, \theta_j \right)$ 的偏导
公式中,学习速率决定了参数值变化的速率即”走多少距离“,而偏导这部分决定了下降的方向即”下一步往哪里“走(当然实际上的走多少距离是由偏导值给出的,学习速率起到调整后决定的作用),收敛处的局部最小值又叫做极小值,即”陆地“。

注意,在计算时要批量更新 $\theta$ 值,即如上图中的左图所示,否则结果上会有所出入,原因不做细究。
2.6 梯度下降直观理解(Gradient Descent Intuition)
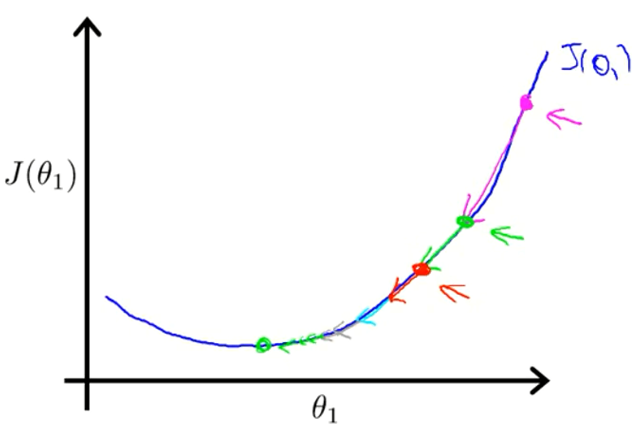
该节探讨 $\theta_1$ 的梯度下降更新过程,即 $\theta_1 := \theta_1 - \alpha\frac{d}{d\theta_1}J\left(\theta_1\right)$。
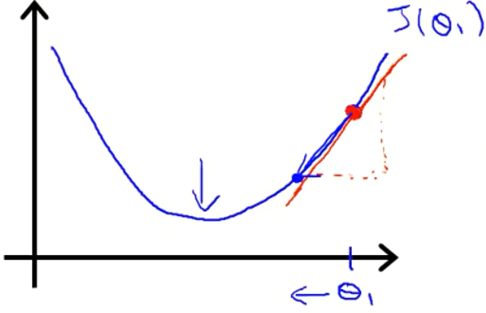
直线的斜率,表示了函数 $J\left(\theta\right)$ 在初始点处有正斜率,也就是说它有正导数,会向左边移动。不断重复,直到收敛。
初始 $\theta$ 值(初始点)是任意的。
对于学习速率 $\alpha$,需要选取一个合适的值才能使得梯度下降算法运行良好。
学习速率过小图示:
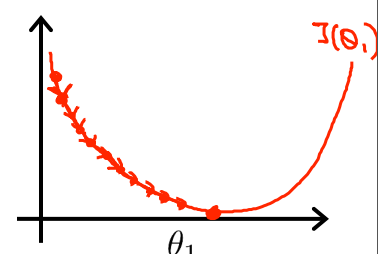
收敛的太慢,需要更多次的迭代。
学习速率过大图示:
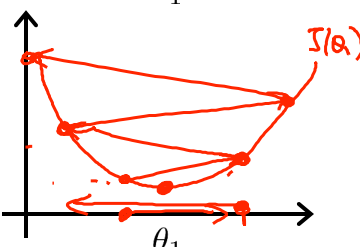
可能越过最低点,甚至导致无法收敛。
学习速率只需选定即可,不需要动态改变,随着斜率越来越接近于0,代价函数的变化幅度会越来越小,直到收敛到局部极小值。
代价函数随着迭代的进行,变化的幅度越来越小。
2.7 线性回归中的梯度下降(Gradient Descent For Linear Regression)
线性回归模型
- $h_\theta(x)=\theta_0+\theta_1x$
- $J\left( \theta_0, \theta_1 \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{ { {\left( { {h}_{\theta } }\left( { {x}^{(i)} } \right)-{ {y}^{(i)} } \right)}^{2} } }$
梯度下降算法
$$
\begin{split}
& \text{Repeat until convergence:} \; \lbrace \\
&{ {\theta }_{j} }:={ {\theta }_{j} }-\alpha \frac{\partial }{\partial { {\theta }_{j} } }J\left( {\theta_{0} },{\theta_{1} } \right) \\
\rbrace
\end{split}
$$
直接将线性回归模型公式代入梯度下降公式可得出公式

当 $j = 0, j = 1$ 时,线性回归中代价函数求导的推导过程(:
$$
\begin{split}
\frac{\partial}{\partial\theta_j} J(\theta_1, \theta_1)&=\frac{\partial}{\partial\theta_j} \left(\frac{1}{2m}\sum\limits_{i=1}^{m}{ {\left( { {h}_{\theta } }\left( { {x}^{(i)} } \right)-{ {y}^{(i)} } \right)}^{2} } \right)\\
&=\left(\frac{1}{2m}*2\sum\limits_{i=1}^{m}{ {\left( { {h}_{\theta } }\left( { {x}^{(i)} } \right)-{ {y}^{(i)} } \right)} } \right)*\frac{\partial}{\partial\theta_j}{ {\left( { {h}_{\theta } }\left( { {x}^{(i)} } \right)-{ {y}^{(i)} } \right)} } \\
&=\left(\frac{1}{m}\sum\limits_{i=1}^{m}{ {\left( { {h}_{\theta } }\left( { {x}^{(i)} } \right)-{ {y}^{(i)} } \right)} } \right)*\frac{\partial}{\partial\theta_j} {\left( \theta_0 + \theta_1{x_1^{(i)} }-{ {y}^{(i)} } \right)}
\end{split}
$$
所以当 $j = 0$ 时:
$$
\frac{\partial}{\partial\theta_0} J(\theta)=\frac{1}{m}\sum\limits_{i=1}^{m}{ {\left( { {h}_{\theta } }\left( { {x}^{(i)} } \right)-{ {y}^{(i)} } \right)} }
$$
所以当 $j = 1$ 时:
$$
\frac{\partial}{\partial\theta_1} J(\theta)=\frac{1}{m}\sum\limits_{i=1}^{m}{ {\left( { {h}_{\theta } }\left( { {x}^{(i)} } \right)-{ {y}^{(i)} } \right)} } *x_1^{(i)}
$$
上文中所提到的梯度下降,都为批量梯度下降(Batch Gradient Descent),即每次计算都使用所有的数据集 $\left(\sum\limits_{i=1}^{m}\right)$ 更新。
由于线性回归函数呈现碗状,且只有一个全局的最优值,所以函数一定总会收敛到全局最小值(学习速率不可过大)。同时,函数 $J$ 被称为凸二次函数,而线性回归函数求解最小值问题属于凸函数优化问题。
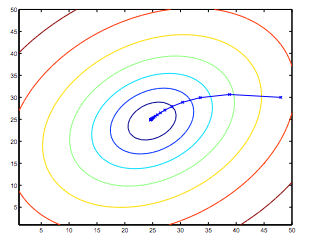
另外,使用循环求解,代码较为冗余,后面会讲到如何使用向量化(Vectorization)来简化代码并优化计算,使梯度下降运行的更快更好。